Принцип суперпозиции. т.е. напряженность поля любого числа точечных зарядов в данной точке равна векторной сумме напряженностей полей

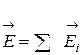, (6)

т.е. напряженность поля любого числа точечных зарядов в данной точке равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности в этой точке. Принципом суперпозиции удобно пользоваться при расчете поля сравнительно небольшого числа дискретных зарядов. В случае непрерывного распределения зарядов расчет поля с помощью этого универсального метода становится громоздким. В этом случае часто удобнее воспользоваться теоремой Гаусса. Она формулируется следующим образом: поток вектора напряженности электрического поля через любую воображаемую замкнутую поверхность S равен в вакууме отношению алгебраической суммы зарядов, заключенных внутри этой поверхности, к электрической постоянной e_о:

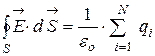, (7)

где N - количество зарядов внутри замкнутой поверхности S.

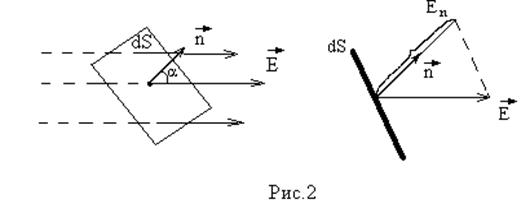
Потоком вектора напряженности dФ_Е через элементарную плоскую площадку dS называется величина равная

.

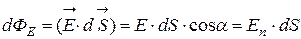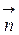- нормаль к площадке dS; Е_n - проекция вектора 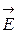на направление нормали к площадке dS

.

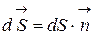При наличии диэлектриков теорема Гаусса записывается в виде

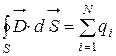, (8)

где N - количество сторонних зарядов внутри замкнутой поверхности S.

Вектор 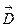называется вектором электрического смещения

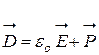, (9)

где 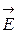- суммарная напряженность полей, созданных сторонними и связанными зарядами в диэлектрике, 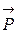- поляризованность диэлектрика:

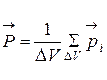, (10)

где 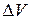- физически бесконечно малый объем; 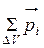- сумма дипольных электрических моментов молекул, составляющих этот объем диэлектрика. Линии вектора 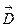начинаются и заканчиваются на сторонних зарядах. В точках без сторонних зарядов они непрерывны, включая точки со связанными зарядами. Иными словами, поток вектора 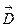определяется только сторонними зарядами, но при таком их распределении, которое возникает в присутствии диэлектрика.

Для изотропных диэлектриков любого типа поляризованность связана с напряженностью поля в той же точке простым соотношение

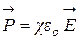, (11)

где: 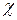- диэлектрическая восприимчивость.

Подставив (11) в (10), получим

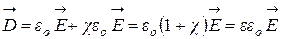, (12)

где: 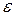- относительная диэлектрическая проницаемость диэлектрика.

Величина 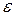показывает, во сколько раз ослабляется электрическое поле внутри однородного диэлектрика по сравнению с полем в вакууме.