Классификация задач и пути из решения
Задачи этой темы можно разделить на четыре типа:
1. Задачи, в которых рассматривается взаимодействие точечного и распределенного зарядов.
2. Задачи, в которых рассматривается взаимодействие точечного и распределенного зарядов.
3. Задачи, в которых требуется определить напряженность электрического поля по известным величинам и распределению зарядов.
4. Задачи, в которых рассматривается взаимодействие распределенных зарядов.
Среди задач первого типа интерес представляют задачи, в которых взаимодействующие точечные заряды находятся в состоянии равновесия. Они решаются путем применения закона Кулона и принципа суперпозиции. При этом последовательность операций должна быть следующей:
1. Сделать рисунок и провести идеализацию рассматриваемой в задаче физической системы.
2. Выбрать какой-либо заряд и указать на рисунке действующие на него силы.
3. Для выбранного заряда записать в векторной форме уравнение 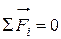 , где
, где 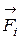 - силы, действующие на выбранный заряд.
- силы, действующие на выбранный заряд.
4. Спроектировав полученное выше векторное уравнение на выбранное направление, получить уравнение в скалярной форме. За выбранное обычно принимается направление, вдоль которого силы действуют в противоположных направлениях.
5. Подставить в полученное выше скалярное уравнение выражения для сил по закону Кулона и, исходя из геометрических соображений, преобразовать его таким образом, чтобы осталась только одна неизвестная величина.
6. Решить уравнение с одним неизвестным.
Задачи второго типа могут быть решены двумя методами.
Первый состоит в применении закона Кулона и принципа суперпозиции.
Второй заключается в нахождении любым путем напряженности поля, создаваемого распределенным зарядом в точке, где находится точечный заряд q , и вычислении силы из соотношения 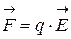 , т.е. по существу сводится к решению задачи третьего типа, а потому отдельно мы его рассматривать не будем.
, т.е. по существу сводится к решению задачи третьего типа, а потому отдельно мы его рассматривать не будем.
При решении задач первым методом можно руководствоваться следующим алгоритмическим предписанием:
1. Сделать рисунок и провести идеализацию рассматриваемой в задаче физической системы.
2. Разделить заданный линейный, поверхностный или объемный заряд на такие элементы, чтобы находящийся на них заряд соответственно 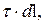
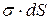 и
и 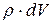 можно было считать точечным.
можно было считать точечным.
3. Выбрать какой-либо из элементов и по закону Кулона записать выражение для силы, действующей с его стороны на заданный точечный заряд.
4. Указать вектор этой силы на рисунке и разложить его на перпендикулярную (по отношению к распределенному заряду) и параллельную составляющие. Для каждой из составляющих записать закон Кулона.
5. Выбрать переменную интегрирования и определить пределы, в которых она изменяется. При этом за переменную интегрирования следует принимать величину, определяющую положение выбранного элемента 
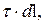
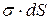 и
и 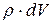 относительно точечного заряда.
относительно точечного заряда.
6. Из геометрических соображений выразить величины, входящие в уравнения для перпендикулярной и параллельной составляющих, через известные и переменную интегрирования и полученный результат подставить в эти уравнения.
7. Интегрируя уравнения, полученные в пункте 6 по переменной интегрирования с учетом пределов, найденных в пункте 5, определить величины перпендикулярной и параллельной составляющих.
8. Суммируя векторно перпендикулярную и параллельную составляющие, определить силу, действующую на точечный заряд со стороны распределенного.
Задачи третьего типа могут быть решены тремя методами.
1. Путем использования принципа суперпозиции.
2. Применением теоремы Гаусса.
3. Путем вычисления потенциала с последующим нахождением напряженности из уравнения 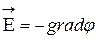 .
.
В принципиальном смысле все эти методы равноценны, в практическом - в зависимости от конкретных обстоятельств различны, так как связаны с неодинаковым объемом вычислительной работы. Поскольку тема «Потенциал» рассматривается после этой, здесь мы ограничимся рассмотрением только первых двух методов.
Первый принципиально позволяет найти напряженность поля любой системы зарядов. Практически он удобен при нахождении напряженности поля, созданного системой относительно небольшого числа дискретных зарядов. При вычислении же напряженностей полей, созданных распределенными зарядами, его применение связано, как правило, с большим объемом вычислений. Алгоритм решения задач этим методом показан на рис.3.
| Создать рисунок и определить модель заряда (точечный, линейный, поверхностный или объемный), создающего поле | ||
| Если система точечных зарядов | Если заряд распределенный | |
1.По формуле 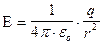 определить величины напряженности, создаваемой каждым из зарядов в данной точке определить величины напряженности, создаваемой каждым из зарядов в данной точке
| 1.Разделить заданный заряд на такие элементы, чтобы находящийся на них заряд можно было считать точечным | |
2.Указать на рисунке величину и направление векторов напряженности 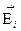 , создаваемых в данной точке каждым из зарядов, и, производя их векторное суммирование, найти , создаваемых в данной точке каждым из зарядов, и, производя их векторное суммирование, найти 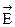
| 2.Выбрать какой-либо из элементов и записать выражение для напряженности, создаваемой им в данной точке | |
3.Вычислить величину 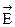 по теореме косинусов по теореме косинусов
| 3.Указать вектор этой напряженности на рисунке и разложить его на составляющие. Записать уравнения, описывающие каждую из составляющих | |
| 4.Выбрать переменную интегрирования и определить пределы, в которых она изменяется. За переменную интегрирования следует принимать величину, определяющую положение выбранного элемента относительно данной точки | ||
| 5.Из геометрических соображений выразить величины, входящие в уравнения для составляющих, через известные и переменные интегрирования и полученный результат подставить в эти уравнения | ||
| 6.Интегрируя уравнения, найденные в предыдущем пункте по переменной интегрирования с учетом выше найденных пределов, определить величины составляющих | ||
| 7.Суммируя их векторы, найти напряженность поля в данной точке | ||
Рис.4
Обратите внимание, что только что приведенный алгоритм решения задач третьего типа для случая распределенного заряда по существу тождествен алгоритму решения задач второго типа первым методом. Однако для Вашего удобства мы привели его отдельно.
Второй метод, базирующийся на применении теоремы Гаусса, наиболее эффективен в тех случаях, когда заряженные тела обладают ярко выраженной симметрией. В общем же случае вычисления оказываются чрезвычайно сложными. Поэтому практически он применяется либо для вычисления напряженностей полей заряженных тел симметричной формы (плоскости, шары, цилиндры), либо заряженных тел, форма которых может быть аппроксимирована телами симметричной формы.
При вычислении напряженности поля этим методом можно использовать следующий алгоритм.
1. Сделать рисунок и указать на нем направления векторов напряженности.
2. Построить на рисунке поверхность, через которую будет определяться поток вектора 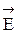 . При ее построении следует руководствоваться правилом: элементы поверхности должны быть либо перпендикулярны либо параллельны линиям напряженности.
. При ее построении следует руководствоваться правилом: элементы поверхности должны быть либо перпендикулярны либо параллельны линиям напряженности.
3. Определить напряженность поля 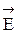 из формулы (7). При этом в левую часть следует подставлять произведение
из формулы (7). При этом в левую часть следует подставлять произведение 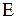 на площадь поверхности, пересекаемой линиями напряженности, а в правую - полный заряд, заключенный внутри выбранной поверхности. Полный заряд для случаев объемного, поверхностного либо линейного зарядов определяется как произведение соответствующей плотности заряда на объем, поверхность или длину, заключенные внутри поверхности, через которую вычисляется поток.
на площадь поверхности, пересекаемой линиями напряженности, а в правую - полный заряд, заключенный внутри выбранной поверхности. Полный заряд для случаев объемного, поверхностного либо линейного зарядов определяется как произведение соответствующей плотности заряда на объем, поверхность или длину, заключенные внутри поверхности, через которую вычисляется поток.
В случае, если поле создается системой распределенных зарядов, то напряженность поля, создаваемого каждым из распределенных зарядов, можно определить с помощью рассмотренных выше методов. Суммарную же напряженность можно найти, используя принцип суперпозиции.
Конечные формулы для расчета напряженностей полей наиболее часто встречающихся форм источников приведены в табл. 1.
Задачи четвертого типа решаются, исходя из соотношения
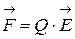 (13)
(13)
где Q - величина данного распределенного заряда, а 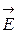 -напряженность поля, создаваемого другим распределенным зарядом (или зарядами), т.е. решение задачи в этом случае, по существу, сводится к решению задачи третьего типа.
-напряженность поля, создаваемого другим распределенным зарядом (или зарядами), т.е. решение задачи в этом случае, по существу, сводится к решению задачи третьего типа.
Таблица 1
| Геометрия источника поля | Напряженность в вакууме |
| Точка | 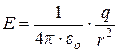
|
Бесконечная плоскость, равномерно заряженная с поверхностной плотностью 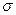
| 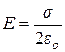
|
Две разноименно заряженные с поверхностной плотностью 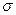 бесконечные плоскости (область между пластинами) бесконечные плоскости (область между пластинами)
| 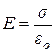
|
Равномерно заряженный с линейной плотностью 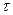 цилиндр радиусом R ( r³ R<<h),
где h - высота цилиндра цилиндр радиусом R ( r³ R<<h),
где h - высота цилиндра
| 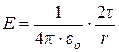
|
| Равномерно объемно заряженный шар радиусом R (r £ R) | 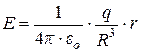
|
Если поле неоднородно, использовать соотношение (13) нельзя. Задачи в этом случае решаются методом суперпозиции. Алгоритм решения может быть следующим.
1. Сделать рисунок и определить модели взаимодействующих зарядов.
2. Выбрать распределенный заряд, находящийся в поле, и распределенный заряд, создающий поле. Если один из зарядов конечен, то удобнее именно его рассматривать находящимся в поле.
3. Разделить находящийся в поле заряд на такие элементы, чтобы заряд каждого элемента можно было считать точечным. Выделить какой-либо элемент и по закону Кулона записать выражение для силы, действующей на него со стороны создающего поле заряда.
4. Выбрать переменную интегрирования и определить пределы ее изменения. В качестве переменной интегрирования следует брать величину, от которой зависит сила, действующая на каждый элемент.
5. Указать на рисунке вектор силы, действующей на выделенный элемент, и разложить его на взаимно перпендикулярные составляющие. Записать уравнения, описывающие каждую из составляющих, выразив в них неизвестные величины через известные и переменную интегрирования.
6. Интегрируя уравнения, найденные в п.5 с учетом найденных выше пределов, определить величины составляющие силы.
7. Суммируя их векторно, определить силу взаимодействия распределенных зарядов.
В заключение отметим, что если в задачах рассматриваются явления электростатической индукции и поляризации, то система зарядов оказывается часто заданной неявно. В них, прежде чем перейти к решению с использованием приведенных выше алгоритмов, необходимо, используя знания об этих явлениях, установить заданную систему зарядов.
Дата добавления: 2015-02-16; просмотров: 774;
