РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Полный вектор напряженности магнитного поля Т= 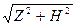ориентирован по наклонению J магнитного поля, и, следовательно, зависимость его при перемещении по профилю является сложной. Если Z_н и H_н ‑ нормальные и Z_а и Н_а ‑ аномальные значения, то Т можно выразить так:

T = 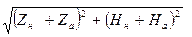. (6.15)

Разность векторов Δ T_i= Т_i – Т_н в текущей точке профиля х_i и в опорном пункте x₀ представим в виде:

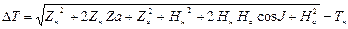(6.16)

Преобразуя формулу (6.16), получим

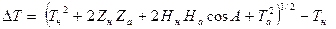, (6.17)

где А – угол между Н_о и Н_а.

Вводя параметры нормального J_н и аномального J_а наклонения, а также учитывая склонение D_н и D_а, получим

,

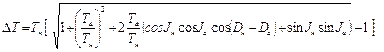Разложение радикала в формуле (6.17) в ряд по степеням Т_а / Т_н приводит к приближенной формуле

ΔТ² =Z²_a+(H_a cos A)².

Связь между вектором Т и его составляющими изображена на рис.6.2,а, в, с. Угол между векторами равен разности наклонений. От величины этой разности существенно зависят величина аномального вектора Т_а и разность модулей ΔТ. Как известно, на практике измеряется именно модуль полного вектора Т.

Если учесть зависимость ΔТ от нормального наклонения J, то можем, согласно (рис.6.5,в), написать

ΔТ = Z_a sin J + H_a cos J cos A. (6.18)

Поскольку модульные измерения не несут в себе информации об угловых характеристиках аномального магнитного поля, при обработке полевых данных ограничиваются вычислением аномалий ΔТ, определяемых как скалярная разность модулей векторов Т_i и Т_н.

Из формулы (6.18) следует, что ни основной элемент поля Т_а, ни аномалия ΔТ не являются гармоническими функциями координат. Величины Т_а и ΔТ тождественно равны между собой лишь при равенстве угловых характеристик D_н = D_a и J_н = J_a; в противном случае Т_а не равно ΔТ, причем различия могут быть весьма существенны. При изменении наклонения на 1° разность ΔТ изменяется на 600-1000 нТл. При аэромагнитной съемке, когда расстояния между опорными пунктами достигают нескольких километров, изменения разности могут быть значительными, следовательно, их необходимо учитывать.

0 0 Н_н Н_а НcosA

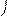
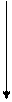
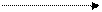
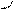x x x

_∆ J _{∆ T} J J

T_{0 Zн}

Т_а Т

Z_а Т Z T

z z z

а в с

Рис.6.2. Связь между вектором Т и его составляющими

При детальной наземной съемке опорный пункт должен находиться на площади, на которой выполняется съемка, и тогда существованием вектора Т_а можно пренебречь, считая, что T_i и Т_о по направлению совпадают (рис.6.2,в).

На широте Перми (φ =56˚) наклонение J =73˚, и, следовательно, формулу (6.18) можно конкретизировать:

ΔТ = 0,956 Za + 0,292 Ha cos A.

График ΔТ по профилю зависит от соотношения значений Z_a и Н_а. Судя по коэффициентам, влияние Н_а почти в 3 раза меньше, чем Z_a. Однако нечетная функция Н_а, представленная антисимметричным графиком, вносит свою коррекцию в четную функцию Z_a. Вследствие этого график ΔТ для средних широт приобретет некоторую асимметрию, станет сложным. Для районов высоких широт земного шара, где наклонение J близко к 90⁰, аномалии ΔТ по виду очень близки аномальным кривым Z_а. Для южных районов России вид аномального графика ΔТ близок виду антисимметричной функции Н_а. Интерпретация таких кривых затруднительна.

Формула (6.18) справедлива с точностью до 2% при Т_а ≤ 0,04 Т₀ (~ 2000 нТл) и с точностью до 5% при Т_а ‹ 0,1 Т₀ (~5000 нТл).

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ