Усовершенствованный метод Эйлера

Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Используются два способа такой аппроксимации. Первый называется «усовершенствованным» методом Эйлера, второй - «модифицированным» методом Эйлера.

Геометрическая интерпретация усовершенствованного метода приведена на рис.7.6.

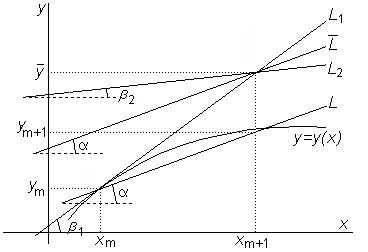
Рис.7.6. Усовершенствованный метод Эйлера

Прямая L₁ есть касательная к истинной кривой y=y(x) в точке (x_m, y_m). Ее наклон к оси OX равен углу 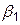, для которого

,

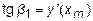или в силу (7.2):

.

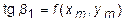Прямая L₂ есть касательная к решению уравнения (7.2) в точке 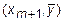, являющейся пересечением L₁ c прямой x = x_m+1. Наклон L₂ равен углу 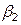, для которого

.

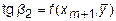Прямая 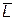проходит через точку 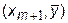, а ее угол наклона равен 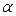, для которого

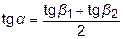или .

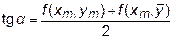Прямая L параллельна 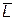и проходит через точку (x_m, y_m), а ее пересечение с x = x_m+1 как раз и определяет окончательное значение y_m+1.

Данное геометрическое построение в аналитическом виде выглядит следующим образом: сначала вычисляется значение 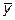функции y(x) в точке x_m+1 по методу Эйлера:

,

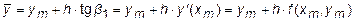(7.7)

а затем оно используется для вычисления 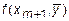, т.е. приближенного значения производной в конце интервала (x_m,x_m+1):

.

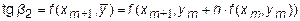Вычислив среднее между этим значением производной и ее значением f(x_m, y_m) в начале интервала, найдем более точное значение y_m+1:

.

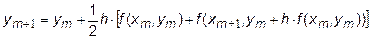(7.8)

Формула (7.8) представляет собой вычислительный алгоритм усовершенствованного метода Эйлера.

Принцип, на котором основан усовершенствованный метод Эйлера, можно пояснить

и иначе. Для этого в разложении (7.3) функции в ряд Тейлора в окрестности точки x_m сохраним член, содержащий h², и отбросим члены более высоких порядков:

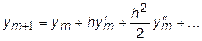
(7.9)

Однако, чтобы сохранить член с h² надо знать вторую производную y"(x_m). Ее можно аппроксимировать конечной разностью :

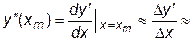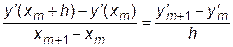
(7.10)

Подставив это выражение в ряд Тейлора (7.9) и заменяя 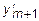его приближением по методу Эйлера, найдем

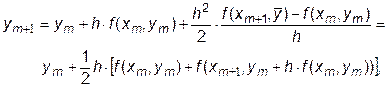
(7.11)

что совпадает с полученным в (7.8) выражением.

Этот метод является методом второго порядка, так как в нем используется член ряда Тейлора, содержащий h². Ошибка метода на каждом шаге имеет порядок h³.

На рис.7.7 приведена блок-схема алгоритма усовершенствованного метода Эйлера.

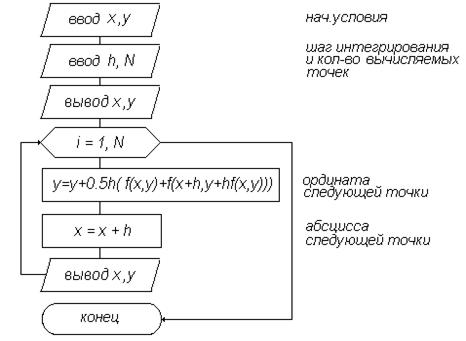
Рис.7.7. Алгоритм усовершенствованного метода Эйлера