Расчёт ленточных фундаментов под ряды колонн по методу местных упругих деформаций

Метод местных упругих деформаций основан на гипотезе Винклера, которая предполагает, что величина осадки грунта в какой-либо точке основания s прямо пропорциональна давлению p, приложенному к этой точке, и не зависит от осадки других точек:

,

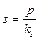где k_s — коэффициент упругости основания, именуемый коэффициентом постели (10…30 Н/см³).

Как показали исследования, данная гипотеза даёт достаточно достоверные результаты для слабых грунтовых оснований с модулем деформации грунта E_gr = 5…20 МПа, подстилаемых малосжимаемыми грунтами с E_gr ≥ 100 МПа (скальный грунт). В этом случае при загружении основания грунт за пределами фундамента практически не оседает. Критерием этого является отношение глубины сжимаемой толщины Н_с к ширине подошвы фундамента b_f , которое должно составлять менее 0,4.

,

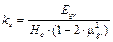где

E_gr — модуль деформации грунта;

Н_с — глубина сжимаемой толщи;

μ_gr — коэффициент Пуассона грунта.

Согласно гипотезе Винклера ленточный фундамент под ряд колонн рассчитывают как балку на упругом основании. В связи с этим используют принцип суперпозиции, когда полные эпюры отпора грунта, изгибающих моментов и поперечных сил находят суммированием решений, полученных для каждого из грузов (N_i , M_i) в отдельности (рис. 24).

Для балки на упругом основании погонное давление со стороны грунта в месте фиксированном расстоянием х от её края равно:

.

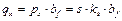Продифференцируем это выражение дважды и учтём ряд зависимостей, известных из сопротивления материалов:

, , , .

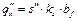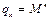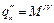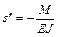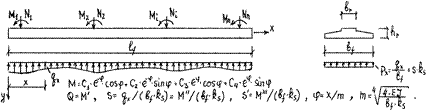
Рис. 24. Расчётные схемы ленточного фундамента под ряды колонн по методу местных упругих деформаций

Тогда получим дифференциальное уравнение изогнутой оси балки:

,

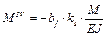или 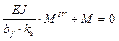, или ,

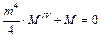где 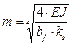— линейная характеристика балки на упругом основании, м.

Общее решение дифференциального уравнения имеет вид:

,

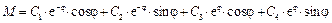где

,

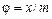x — текущая координата,

С₁, С₂, С₃, С₄ — постоянные интегрирования.

Значения постоянных интегрирования получают, рассматривая граничные условия при нагружении балки тем или иным грузом (N_i или M_i). С этой же целью используют выражения для поперечной силы Q = M′, осадки грунта 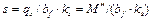и угла поворота фундаментной ленты 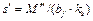. При этом в зависимости от соотношения линейной характеристики балки m и её пролета l различают длинные фундаментные балки (l/m ≥ 3), короткие (0,75 < l/m < 3) и жёсткие (l/m ≤ 0,75).

Для длинных балок постоянные интегрирования С₁, С₂, С₃, С₄ получают, рассматривая четыре схемы нагружения (рис. 25). При этом за положительное принимают направление поперечной силы снизу вверх.

Для коротких балок решение дифференциального уравнения с использованием граничных условий приводит к громоздким формулам. Между тем, в практике проектирования ленточных фундаментов короткие балки встречаются значительно реже, чем жёсткие и длинные. Поэтому в технической литературе рассматривается решение лишь одной из практически важных задач: загружение балки двумя симметрично расположенными на ней сосредоточенными грузами (рис. 26, а). Результаты приближенного решения имеют вид, представленный на рис. 26, б. После определения эпюры осадок погонное давление со стороны грунта вычисляют по формуле

.

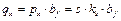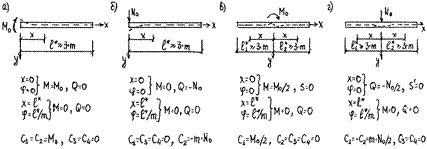
Рис. 25. Расчётные схемы нагружения длинных балок

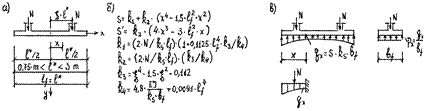
Рис. 26. К расчёту короткой балки: а – схема нагружения, б – основные зависимости, в – эпюра отпора грунта и расчётная схема

Изгибающие моменты и поперечные силы определяют как в консольной балке от внешней нагрузки и отпора грунта. В отличие от метода прямолинейной эпюры, в данном случае эпюра отпора грунта не является линейной, так как нелинейной является эпюра осадок s. При этом, начиная с левого конца фундаментной ленты, вводят условную заделку и рассматривают все нагрузки, расположенные левее заданного сечения.

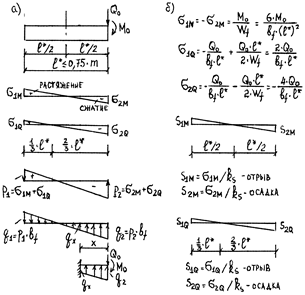
Рис. 27. Расчёт жёстких балок: а – схемы нагружения, б – эпюры давления на грунт, отпора грунта и осадок

Дляжёстких балок их изгибными деформациями пренебрегают и давление по подошве определяют по формулам сопротивления материалов. При этом рассматривают две схемы нагружения: сосредоточенный изгибающий момент М₀ и поперечная сила Q₀ на конце балки (рис. 27). Используя эти схемы, определяют как давление на грунт, так и осадки основания.

Из полученных решений для длинных и жёстких балок можно определить соответствующие коэффициенты влияния перемещений для загруженного конца каждой балки: угла поворота (а₁₁, а₁₂, а′₁₁, а′₁₂) и осадки (а₂₁, а₂₂, а′₂₁, а′₂₂) от единичных воздействий. Расчётные схемы и формулы для вычисления указанных коэффициентов представлены на рис. 28. При этом коэффициенты влияния перемещений принимают со знаком «+», если направление перемещения совпадает с направлением единичного воздействия.В противном случае их принимают со знаком «–».

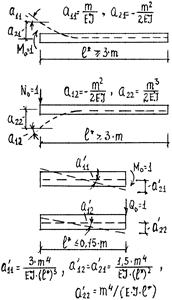
Рис. 28. Расчётные схемы и коэффициенты влияния перемещений для загруженного конца длинных и жёстких балок

Значения указанных коэффициентов влияния перемещений используют для решения задач с комбинированными схемами, которые образуются сочетанием жёстких и длинных балок. К задачам такого типа относится расчёт концевого участка фундаментной ленты (рис. 29, а) и расчёт узла сопряжения фундаментной балки с колонной при большой ширине последней (сборная колонна при её стаканном сопряжении с фундаментной балкой, рис. 29, б). В месте сопряжения балок производят условный разрез и прикладывают неизвестные усилия: изгибающий момент М₀ и перерезывающую силу Q₀ . Их значения находят из условия отсутствия взаимных перемещений краёв балок. Эти условия выражаются системой уравнений:

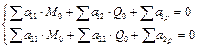
где

Σ а₁₁ — сумма краевых перемещений (углов поворота) длинной и жёсткой балок от М₀ = 1;

Σ а₁₂ — то же, но от Q₀ = 1;

Σ а₂₁ — сумма краевых перемещений (осадок) длинной и жёсткой балок от М₀ = 1;

Σ а₂₂ — то же, но от Q₀ = 1;

Σ а_1p — сумма краевых перемещений (углов поворота) длинной и жёсткой балок от внешнего изгибающего момента;

Σ а_2p — то же, но от внешней вертикальной нагрузки.

Как уже отмечалось, полные эпюры q, M, Q в фундаментной ленте длиной l_f получают в результате суммирования соответствующих решений, полученных для каждого внешнего воздействия M_i , N_i , а также М₀ и Q₀ (рис. 30).

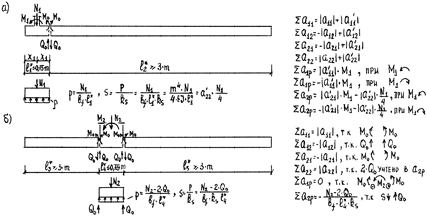
Рис. 29. Комбинированные схемы расчёта ленточных фундаментов под ряды колонн: а – концевой участок фундаментной балки, б – узел сопряжения фундаментной балки с колонной при большей ширине последней

Рис. 30. Расчётные схемы для определения полных эпюр отпора грунта q, изгибающих моментов М и поперечных сил Q в ленточных фундаментах под ряды колонн

При расчёте перекрёстных ленточных фундаментов под ряды колонн возникает дополнительная задача о расчёте узла, состоящего из жёсткого подколонника и четырёх длинных балок. Здесь также производят условные разрезы в местах соединения длинных балок и жёсткого подколонника и прикладывают неизвестные усилия M₀ и Q₀. Их значения находят, решая аналогичную приведенной выше систему двух уравнений с двумя неизвестными. Расчётная схема такого узла и значения коффициентов влияния перемещений приведены на рис. 31. После того, как M₀ и Q₀ будут вычислены, рассматривают два следующих загружения: длинные балки с приложенными на их концах усилиями M₀ и Q₀, и жёсткая балка (подколонник) с приложенными усилиями M₀, Q₀ и внешней нагрузкой. Решая задачу, определяют эпюры отпора грунта и находят эпюры изгибающих моментов и поперечных сил, которые в дальнейшем суммируют с эпюрами от других внешних воздействий на фундамент.

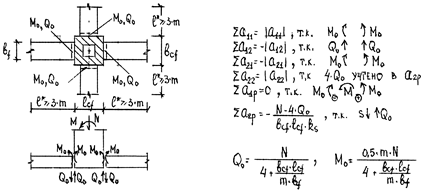
Рис. 31. Расчётные схемы перекрёстных ленточных фундаментов под ряды колонн

ЛЕКЦИЯ 10