Расчёт ленточных фундаментов под ряды колонн по методу общих упругих деформаций. Армирование ленточных фундаментов

Метод общих упругих деформаций основан на гипотезе упругого полупространства, согласно которой основание работает как сплошная однородная упругая среда, ограниченная сверху плоскостью и бесконечно простирающаяся в стороны и вниз. Деформативные свойства упругой среды характеризуются величиной модуля деформации грунта E_gr , который, в отличие от коэффициента постели k_s, не зависит от величины нагрузки под подошвой фундамента, а также величиной коэффициента Пуассона грунта μ_gr . При нагружении такого упругого основания деформации грунта возникают не только в месте приложения нагрузки, но и за её пределами, что и происходит под реальными фундаментами. Метод общих упругих деформаций даёт достоверные результаты для среднесжимаемых грунтов с E_gr = 20…40 МПа и малосжимаемых грунтов с E_gr > 40 МПа в основании, а также при большой суммарной мощности сжимаемых слоёв.

Существует несколько подходов к решению задач с ленточными фундаментами под колонны по методу общих упругих деформаций. Одним из таких подходов является предложенный в 1962 году метод Жемочкина-Синицина (рис. 32). Согласно этому методу непрерывную связь балки с основанием заменяют системой сосредоточенных и абсолютно жёстких стерженьков с их шарнирным соединением с ленточным фундаментом и грунтовым основанием (рис. 32, б). Такие стержни расположены с некоторым шагом Δl , что превращает расчётную схему ленточного фундамента в статически неопределимую систему. В пределах каждого участка Δl реакцию грунта q_j осредняют и усилия в стержнях z_j принимают равными соответствующим равнодействующим давления, теперь уже равномерно распределённого по площади подошвы фундамента, соответствующей каждому стержню (рис. 32, в, г):

.

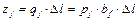Практика проектирования показывает, что необходимая точность расчёта достигается, когда число участков m состоит из 12…16. В этом случае размер каждого элементарного участка принимают в пределах: 0,5∙b_f ≤ Δl ≤ 2∙b_f .

Основную систему получают по смешанному методу расчёта статически неопределимых систем, а именно: балку отделяют от основания, заменяя при этом действие стержней действием неизвестных сил z₁ , z₂ , … z_j , … z_m и вводя условную заделку в конце балки (рис. 32, в). Поэтому неизвестными будут не только указанные силы z_j (j = 1…m), но и осадка заделки y₀ (положительное направление — вниз) и угол её поворота α₀ (положительный — против хода часовой стрелки).

Значения неизвестных находят из решения системы m уравнений совместности деформаций и двух уравнений равновесия:

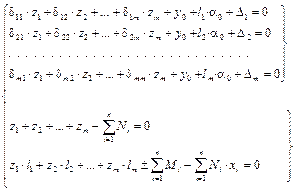
	— уравнения совместности деформаций,
— уравнения равновесия,

где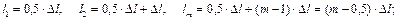

4 Рис. 32. К расчёту ленточного фундамента под ряды колонн по методу общих упругих деформаций: а – схема расположения внешних нагрузок, б – расчётная схема фундаментной ленты, в – основная система смешанного метода расчёта, г – эпюры реактивных давлений грунта, д – перемещение ленты и осадка основания от единичных сил, е – то же, но от осадки и угла поворота условной заделки, ж – эпюры изгибающих моментов от единичных сил и внешних нагрузок

δ_kj — единичное перемещение по направлению искомых неизвестных (перемещение точки k от действия единичной силы, приложенной в точке j). В основной системе оно складывается из двух составляющих: перемещения от прогиба балки v_kj и осадки основания у_kj . Прогиб балки v_kj вычисляют по правилам строительной механики. Соответствующие формулы и примеры расположения единичных сил приведены на рис. 32, ж.

Осадку основания у_kj определяют на основе решения задачи теории упругости о деформировании упругого полупространства (рис. 32, д):

,

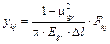где F_kj — функция осадки поверхности основания в точке k при воздействии единичной силы в точке j. Для определения F_kj в технической литературе приведены соответствующие таблицы (В.Н. Байков, Э.Е. Сигалов. «Железобетонные конструкции. Общий курс»).

Грузовое перемещение Δ_j от внешней нагрузки также вычисляют по правилам строительной механики от суммарного действия изгибающих моментов и нормальных сил, приложенных к фундаментной ленте. Соответствующие формулы и примеры расположения внешней нагрузки приведены на рис. 32, ж. Знак минус в этих формулах указывает на то, что направление перемещений от внешней нагрузки противоположно направлению перемещения от единичной силы z_j .

После определения значений неизвестных сил z_j (j = 1…m) вычисляют ординаты эпюры отпора грунта:

.

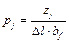Эпюра отпора грунта получается ступенчатой, разрывы в ней сглаживают.

Изгибающие моменты и поперечные силы по длине ленточного фундамента определяют от внешней нагрузки N_i , M_i (i = 1…n) и реактивного давления (отпора) грунта 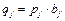как в консольной балке, вводя условную заделку в заданном сечении и рассматривая все нагрузки, расположенные левее такого сечения. По полученным значениям изгибающих моментов и поперечных сил подбирают продольную и поперечную арматуру ребра ленточного фундамента. С этой целью выполняют расчёты на прочность по нормальным и наклонным сечениям фундаментной ленты как неразрезной многопролётной балки таврового сечения с полкой понизу (рис. 33). Рёбра ленточных фундаментов армируют сварными или вязаными каркасами К-1. Количество плоских сварных каркасов определяется шириной ребра b_r: при b_r ≤ 400 мм устанавливают не менее двух каркасов, при 400 < b_r ≤ 800 — не менее трёх, при b_r > 800 мм — не менее четырёх. Плоские сварные каркасы объединяют в пространственный каркас, тем самым увеличивая его жёсткость, с помощью корытообразных или плоских с крюками на концах поперечных стержней сеток С-2 (рис. 33 б, в). При армировании рёбер ленточных фундаментов вязаными каркасами хомуты должны быть замкнутыми, диаметром не менее 8 мм, с шагом не более требуемого по расчёту на поперечную силу и не более 15∙d_s , где d_s — диаметр продольной арматуры. Количество вертикальных ветвей хомутов в поперечном сечении должно быть не менее четырёх при b_r = 400…800 мм, а при b_r > 800 мм — не менее шести.

Диаметр продольной рабочей арматуры ребра ленточного фундамента определяют из его расчёта на действие изгибающего момента. Около 70 % её требуемого количества в нижней зоне устанавливают в пределах ширины ребра, а 30 % распределяют по всей ширине подошвы b_f вместо конструктивной арматуры сетки С-1 (рис. 33).

Процент армирования поперечного сечения ребра фундаментной ленты верхней и нижней продольной рабочей арматурой должен быть не менее минимально допустимого по конструктивным соображениям, учитывающего возможность неравномерного загружения фундамента в процессе возведения здания и неравномерность осадок основания:

, .

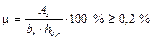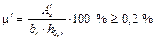Ленточные фундаменты под ряды колоннрассчитывают не только в продольном, но и в поперечном направлении. Здесь расчётным является сечение 1-1, которое проводят по грани ребра ленты. Этот расчёт аналогичен расчёту блок-подушки ленточного фундамента под несущие стены. Его производят, выделяя отрезок фундаментной ленты длиной один метр в зоне максимального значения эпюры отпора грунта. Результатом расчёта является подбор поперечной арматуры сетки С-1.

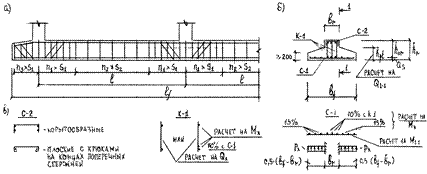
Рис. 33. Армирование ленточного фундамента под ряды колонн: а – продольный разрез, б – поперечный разрез, в – корытообразные и плоские каркасы и сетки

Для ленточных фундаментов в качестве рабочей используют арматуру класса А400 (A-III), а в качестве конструктивной — А240 (A-I). Бетон принимают класса В15 и выше. Под фундаментом устраивают бетонную или песчано-гравийную подготовку. После подбора армирования фундамента выполняют расчёты ленты на продавливание от низа монолитной колонны, подколонника или дна стакана сборной колонны, а также расчёты по образованию и раскрытию трещин.

ЛЕКЦИЯ 11