Метод эквивалентных областей

Под обратной задачей теории магнитного потенциала в математике понимается задача нахождения возмущающего объекта по заданному внешнему потенциалу и намагниченности тела. В практической интерпретации чаще всего сведения о величинах намагниченности отсутствуют. Этим можно объяснить неединственность решения обратной задачи. Разрешению этой проблемы уделяется серьезное внимание.

В работах А.В Цирульского /37/ развивается аппроксимационный подход к интерпретации магнитных полей областями эквивалентных решений. Проблема сводится к нахождению эквивалентного семейства намагниченных однородных областей, которые создают один и тот же внешний магнитный потенциал.

Области, которые с различными намагниченностями создают тождественно равные внешние потенциалы, назвали эквивалентными. Вопросы теории эквивалентности для различных областей исследовались В.Н.Страховым /30/. Он на основе комплексного логарифмического потенциала доказал существование эквивалентных областей, заполненных массами постоянной намагниченности в материальном отрезке (рис. 10.8).

А.В.Цирульским с помощью интеграла типа Коши сконструированы алгоритмы получения семейств однородных эквивалентных областей с различными постоянными намагниченностями для одного или нескольких материальных отрезков с постоянной намагниченностью (рис. 10.9).

В теории А.В.Цирульского /37/ измеренное поле представляется мнимой частью выражения комплексной индукции магнитного поля от суммы нескольких материальных отрезков:

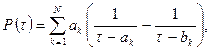(10.18)

где a_k – постоянные комплексные намагниченности отрезков; a_k, b _k - комплексные координаты их концов.

Рис. 10.8. Материальный отрезок (1) и семейство эквивалентных ему областей (2) с постоянной намагниченностью (по В.Н.Страхову)

Поля таких объектов могут быть равны полям, создаваемым областями с постоянными намагниченностями, т.е. для объектов в виде одного или двух материальных отрезков могут существовать семейства эквивалентных решений, непрерывных относительно намагниченности. На рис.10.10 приведено эквивалентное семейство границ раздела магнитных сред, которые с одинаковыми значениями глубины залегания и намагниченности, но с различными ее направлениями создают тождественно равные внешние поля.

Интерпретацию магнитных аномалий ΔТ рекомендуется производить в два этапа. На первом этапе решается система уравнений с минимальным числом отрезков (10.18), параметры которых обеспечивают выполнение условий

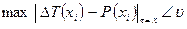; (10.19) ,

где i = 1, 2, …., m – число точек наблюдения.

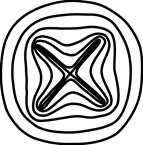
Рис.10.9. Семейство однородных областей, эквивалентных двум пересекающимся отрезкам (по А.В.Цирульскому)

Рис. 10.10. Эквивалентные по внешнему магнитному полю границы раздела двух однородно намагниченных сред и эквивалентная им однородно намагниченная область (по А.В.Цирульскому)

Минимум (10.19) отыскивается соответствующей модификацией градиентного метода при заданных нулевых приближениях параметров отрезков a_k и b_k.

На втором этапе для групп из одного или двух отрезков вычисляются координаты x и z контуров эквивалентных областей с намагниченностями, заданными интерпретатором, т.е. находится семейство эквивалентных решений. Их построение базируется на теории конформных отображений и реализуется путем решения системы трансцедентных уравнений специальными методами.

.

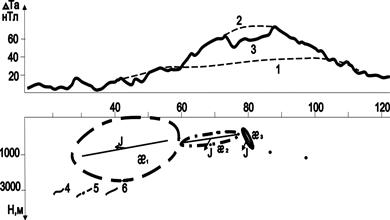
Рис.10.11. Интерпретация магнитного поля методом построения эквивалентных областей при изучении строения осадочной толщи Пермского Прикамья (по Л.А.Гершанок): 1 – региональная аномалия первого порядка, 2 – аномалия второго порядка, 3- аномалия третьего порядка, наблюденное поле, 4 – наблюденное магнитное поле, 5 – граница эквивалентного семейства, 6 – подобранные отрезки

На рис.10.11 приведен пример практической реализации Л.А.Гершанок метода А.В.Цирульского при интерпретации магнитных наблюдений, выполненных с целью изучения строения осадочного чехла в Пермском Прикамье.