Осреднение

Наиболее известным и традиционно распространенным методом разделения магнитных аномалий на региональную и локальную составляющие является метод осреднения. При этом методе цифровая фильтрация осуществляется по специально сконструированным палеткам в скользящем окне либо интервально – по профилям, ориентированным в крест простирания магнитных аномалий. Среднее значение функции в круге радиусом R можно выразить интегралом

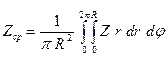
или приближенно суммой

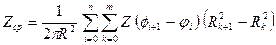. (10.3)

нТл

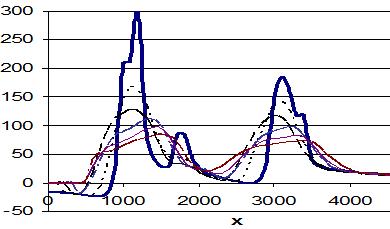
Рис. 10.1. Графики осреднения магнитного поля по профилю в скользящем окне. Размеры усредненного окна: от 5 до 13.

Для двухмерного случая среднее значение функции определяется в скользящем окне по формуле

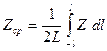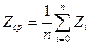или . (10.4)

Осреднение по формуле (10.3) сводится к определению среднего значения исследуемой функции в пределах круга. Для выделения регионального фона радиус выбирают таким, чтобы он превосходил размеры локальных аномалий, подлежащих выделению, и был намного меньше размеров региональных аномалий. На рис.10.1 приведен пример осреднения исходного магнитного поля с различным размером скользящего окна. Если такое условие соблюдено, то при осреднении локальные положительные и отрицательные аномалии в значительной мере компенсируют друг друга, тогда как региональная составляющая будет слабо зависеть от осреднения. Операция осреднения является одним из вариантов определения

а

в

Рис. 10.2. Карты остаточных аномалий магнитного поля при трехмерном осреднении: а – радиус 2.5 км, в – радиус 1 км

Остаточные аномалии, полученные после вычитания из исходной функции данных осреднения, характеризуют поведение локальных аномалий. Степень точности выделения локальной аномалии рекомендуют оценивать по коэффициенту, который называется мерой осреднения. Мера осреднения ε – это отношение осредненного значения поля к его исходному значению:

Осреднение выполняется в автоматическом режиме по радиально-кольцевой или прямоугольной палетке, в каждом секторе которой вычисляется среднее значение поля. Размеры палеток выбираются такими, чтобы в трансформированном поле были подчеркнуты интересующие интерпретатора детали. Операция осреднения отмечает плавно меняющиеся магнитные аномалии и исключает или подавляет аномалии с резкими градиентами.

На рис. 10.2 демонстрируются материалы аэромагнитных съемок масштаба 1 : 50 000, выполненные на территории Пермской области с целью изучения строения осадочной толщи. Полученные карты остаточных аномалий наглядно демонстрируют возможности осредняющей трансформанты: чем меньше радиус осреднения, тем детальнее локализованы магнитные аномалии. А.К.Маловичко /23/ считает, что недостатком метода осреднения является неизбежное искажение полей, вызываемое искусственным перераспределением магнитных свойств возмущающих объектов и появлением фиктивных полей, не соответствующих истинному распределению источников. В связи с этим карты остаточных аномалий после осреднения могут быть использованы в основном при качественном истолковании результатов магнитной съемки.

10.3. Вычисление значений Н по значениямZ

Задача определения Н в математике решается в виде преобразования Гильберта. Функции Z и Н рассматриваются в этом случае в качестве вещественной и мнимой части функции комплексной переменной. В магниторазведке при решении задачи математическая трактовка выполняется на инженерном уровне. Значения Н используются при исследованиях магнитного поля, в частности при интерпретации аномалий. Современных приборов для измерений Н нет. Только в учебниках и справочниках 60-летней давности можно найти описание приборов различных конструкций и методик работы с ними.

Рассмотрим теоретические связи двух составляющих напряженности магнитного поля. Пусть по прямолинейному профилю известны значения составляющей Z. Геологический разрез на территории исследования представляем совокупностью тонких пластов с латеральной изменчивостью их намагниченности. У поверхности Земли геологические образования заменяем слоем породы с магнитной плотностью σ, и тогда дифференциал магнитного момента выразится формулой

dm = σ dx,

а поверхностную плотность можно определить из наблюденных значений

σ = .

В точке Р имеем

dH = 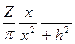dх.

При произвольно взятом начале координат

dH = ,

где x - абсцисса точки Р относительно начала координат. Совмещая точку Р с началом координат и принимая h=0, получим

H = 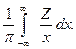(10.5)

В этом интеграле при х=0 появляется бесконечность. В математике такие интегралы называются несобственными или сингулярными, ядро интеграла носит имя математика Коши.

Для вычисления интеграла выделим область от -Δx до Δx, в которой обнаруживается сингулярность и две области: от -∙¥ до -Δx и от +Δx до + ¥. Таким образом,

H = (10.6)

Для вычисления интеграла в пределах от -Δx до Δx предполагаем, что Z= К х, где К – коэффициент, подлежащий определению. Итак,

На концах интервала (+∆х) и (-∆х) имеем Z(∆х) и Z(-∆х), поэтому после подстановок для вычисления сингулярного интеграла получаем формулу

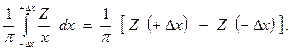(10.7)

Вычисление интегралов от -¥ до -∆х и от ∆х до ¥ производится численными методами, т.е. интервалы разбиваются на небольшие промежутки, на каждом из которых для Z допустимо взять среднее значение и вынести его из-под интеграла.

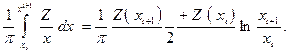
Если обозначить и принять С = 0.314, то

.

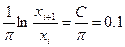Обычно при расчетах используются ∆х, равные 1, 0.5 или 0.25 см. Если начальное значение х=1, то последующие фильтровые значения будут такими: 1.37, 1.87, 2.56, 3.51, 4.80 и т.д. Окончательная формула имеет следующий вид:

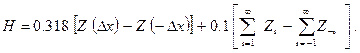(10.8)

Данная трансформация является очень полезной при интерпретации магнитных аномалий. Экспресс-вычисления можно вести в полевых условиях с помощью специальной палетки, учитывающей закон изменения расстояний от начала координат для считывания входной информации. Компьютерная обработка ведется по программам, заимствованным чаще всего из сейсморазведки. Теоретически аналогично решается задача для трехмерного поля. Для вычисления разработана и построена круговая палетка.