Работа и мощность тока. Закон Джоуля-Ленца
Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением 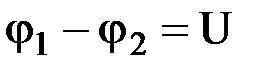 . Так как ток представляет собой перемещение заряда q под действием поля, то работу тока можно определить по формуле
. Так как ток представляет собой перемещение заряда q под действием поля, то работу тока можно определить по формуле 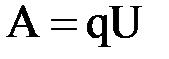 . Учитывая формулу
. Учитывая формулу 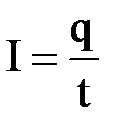 и закон Ома, получим
и закон Ома, получим 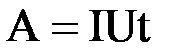 , или
, или 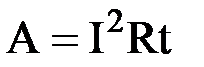 , или
, или 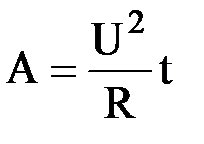 , где t - время протекания тока. Поделив обе части равенства на t, получим выражения для мощности постоянного тока N:
, где t - время протекания тока. Поделив обе части равенства на t, получим выражения для мощности постоянного тока N: 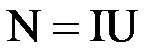 ,
, 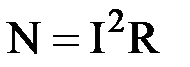 ,
, 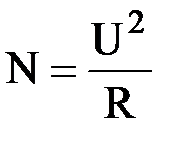 . Работа тока в системе единиц СИ измеряется в доулях (Дж), а мощность - в ваттах (Вт). На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1Вт×ч - работа тока мощностью 1Вт в течение одного часа. 1Вт×ч=3.6×103 Дж.
. Работа тока в системе единиц СИ измеряется в доулях (Дж), а мощность - в ваттах (Вт). На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1Вт×ч - работа тока мощностью 1Вт в течение одного часа. 1Вт×ч=3.6×103 Дж.
Опыт показывает, что ток всегда вызывает некоторое нагревание проводника. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов при каждом их столкновении с ионами металлической решетки переходит в теплоту Q. Если ток идет по неподвижному металлическому проводнику, то вся работа тока расходуется на его нагревание и, следуя закону сохранения энергии, можно записать 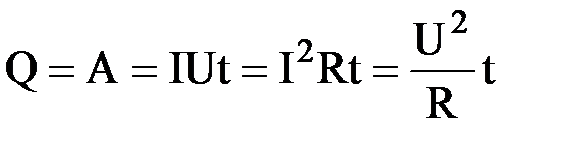 . Данные соотношения выражают закон Джоуля-Ленца. Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э. Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А. Ладыгиным лампы накаливания. На тепловом действии тока основан целый ряд электрических приборов и установок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы - чайники, кипятильники, утюги. Определим удельную тепловую мощность токаw, т.е. количество теплоты, выделяющееся в единице объема за единицу времени. Выделим в проводнике элементарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллельной направлению тока, и сопротивлением
. Данные соотношения выражают закон Джоуля-Ленца. Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э. Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А. Ладыгиным лампы накаливания. На тепловом действии тока основан целый ряд электрических приборов и установок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы - чайники, кипятильники, утюги. Определим удельную тепловую мощность токаw, т.е. количество теплоты, выделяющееся в единице объема за единицу времени. Выделим в проводнике элементарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллельной направлению тока, и сопротивлением  ,
, 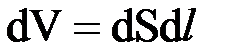 . По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота
. По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота 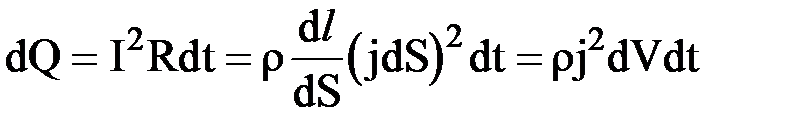 . Тогда
. Тогда 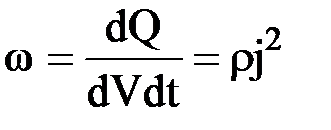 и, используя закон Ома для плотности тока
и, используя закон Ома для плотности тока 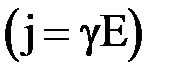 и соотношение
и соотношение 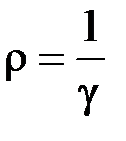 , получим
, получим 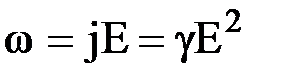 . Эти соотношения выражают закон Джоуля-Ленца в дифференциальной форме.
. Эти соотношения выражают закон Джоуля-Ленца в дифференциальной форме.
Дата добавления: 2015-02-13; просмотров: 1358;
