Закон Ома для участка и полной замкнутой цепи
В 1826 г. немецкий ученый Георг Ом экспериментально установил прямую пропорциональную зависимость между силой тока I в проводнике и напряжением U на его концах: 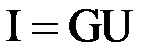 , где G - электрическая проводимость проводника. Величина, обратная проводимости называется электрическим сопротивлением проводника R. Таким образом, закон Ома для участка цепи, не содержащего источника э.д.с., имеет вид
, где G - электрическая проводимость проводника. Величина, обратная проводимости называется электрическим сопротивлением проводника R. Таким образом, закон Ома для участка цепи, не содержащего источника э.д.с., имеет вид 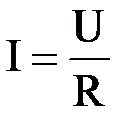 . Учитывая, что в общем случае участок цепи может содержать и э.д.с., закон Ома следует представить в виде
. Учитывая, что в общем случае участок цепи может содержать и э.д.с., закон Ома следует представить в виде  .
.
Сопротивление проводника зависит от его размеров, формы и материала, из которого он изготовлен. Для однородного линейного проводника 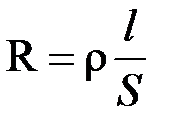 , где l - длина, S - площадь поперечного сечения проводника, r - удельное электрическое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом - это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А.
, где l - длина, S - площадь поперечного сечения проводника, r - удельное электрическое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом - это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А.
Если цепь замкнута, то 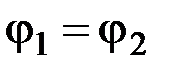 ,
, 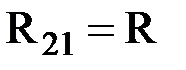 , где R - общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать
, где R - общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать 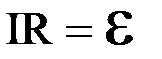 , где e - алгебраическая сумма всех э.д.с., имеющихся в этой цепи.
, где e - алгебраическая сумма всех э.д.с., имеющихся в этой цепи.
 Рисунок 4.1- Отрезок
проводника.
Рисунок 4.1- Отрезок
проводника.
|
Принято называть сопротивление источника тока r - внутренним, а сопротивление всей остальной цепи R - внешним. Окончательный вид формулы закона Ома для замкнутой цепи 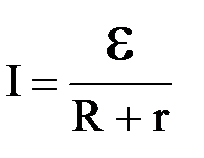 . В системе единиц СИ напряжение и э.д.с. измеряются в Вольтах (В), сопротивление - в Омах (Ом), удельное электрическое сопротивление - в Ом-метрах (Ом×м), электрическая проводимость в Сименсах (См). Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.4.1). Сила тока на этом участке
. В системе единиц СИ напряжение и э.д.с. измеряются в Вольтах (В), сопротивление - в Омах (Ом), удельное электрическое сопротивление - в Ом-метрах (Ом×м), электрическая проводимость в Сименсах (См). Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.4.1). Сила тока на этом участке 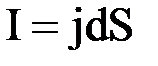 , сопротивление
, сопротивление  , падение напряжения
, падение напряжения  , где Е - напряженность электрического поля в проводнике. Подставив эти параметры в закон Ома для участка цепи, получим
, где Е - напряженность электрического поля в проводнике. Подставив эти параметры в закон Ома для участка цепи, получим 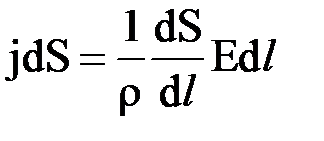 . Отсюда
. Отсюда 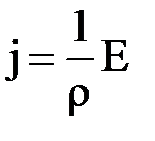 или
или 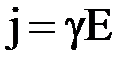 , где
, где  - удельная электрическая проводимость проводникаили удельная электропроводность. В векторном виде имеем
- удельная электрическая проводимость проводникаили удельная электропроводность. В векторном виде имеем 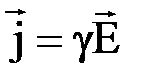 (единицей измерения g в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме: плотность тока в любой точке внутри проводника прямо пропорциональна напряженности поля в этой точке.
(единицей измерения g в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме: плотность тока в любой точке внутри проводника прямо пропорциональна напряженности поля в этой точке.
Дата добавления: 2015-02-13; просмотров: 1654;
