Примеры решения задач. Задача 1. Ток I в проводнике меняется со временем t по уравнению I=4+ 2t, где I − в амперах и t − в секундах
Задача 1. Ток I в проводнике меняется со временем t по уравнению I=4+ 2t, где I − в амперах и t − в секундах. Какое количество электричества q проходит через поперечное сечение проводника за время от t1 = 2c до t2 =6c? при каком постоянном токе I0 через поперечное сечение проводника за то же время проходит такое же количество электричества?
Решение. Из определения сила тока dq = Idt, следовательно
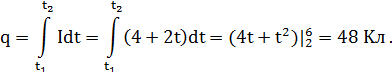
При постоянном токе, 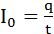 , где t = t2 – t1 = 4c.
, где t = t2 – t1 = 4c.
Подставляя числовые значения, получим I0 = 12А.
Ответ: q = 48 Кл; I0 = 12 А.
Задача 2. Реостат из железной проволоки, амперметр и генератор включены последовательно. При t0 = 0oC сопротивление реостата R0=120 Ом, сопротивление амперметра RА0 = 20 Ом. Амперметр показывает ток I0=22мА. Какой ток I будет показывать амперметр, если реостат нагреется на ΔT=50K? Температурный коэффициент сопротивления железа α=6 10-3K-1.
Решение. Запишем закон Ома для первоначального состояния цепи:
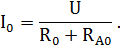
После того как реостат нагрелся, его сопротивление R0 изменилось и стало равным R. Амперметр стал показывать ток
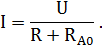
Сопротивление реостата можно найти по формуле
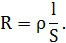
Удельное сопротивление ρ зависит от температуры следующим образом:
ρ = ρ0 (1 + αΔT).
В первоначальном состоянии
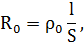
откуда
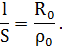
В результате получим
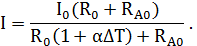
Ответ: I = 17,5мА.
Задача 3. Под конец зарядки аккумулятора при силе тока в цепи I1=3А показание вольтметра, подключённого к зажимам аккумулятора, U1=4,25В. Вначале разрядки того же аккумулятора при силе тока в цепи I2=4А показание вольтметра U2=3,9В. Определить ЭДС 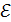 и внутреннее сопротивление r аккумулятора.
и внутреннее сопротивление r аккумулятора.
Решение: Аккумуляторы являются многоразовыми химическими источниками тока. При длительной работе они разряжаются, т.е. их ЭДС уменьшается. Аккумуляторы могут быть вновь заряжены при пропускании электрического тока от внешнего источника в направлении, противоположном стороннему полю аккумулятора. В конце зарядки, так же
как и в начале разрядки (т.е. самостоятельной работы аккумулятора как источника на нагрузку), можно считать, что ЭДС аккумулятора имеет максимальное номинальное значение, которое и требуется определить.
Вольтметр, включённый в цепь, всегда показывает напряжение на себе самом, равное разности потенциалов между точками, к которым он подключён. В данном случае показания вольтметра Рисунок 4.4. К задаче 3 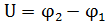 , (при условии, что
, (при условии, что 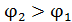 ). Поскольку внутреннее сопротивление вольтметра не задано, следует предположить, что оно настолько велико по сравнению с сопротивлением всех элементов цепи, что силой тока, идущего через вольтметр, можно пренебречь. Тогда сила тока, протекающего через аккумулятор (рис.4.4.), равна заданному значению I1(при разрядке I2).
). Поскольку внутреннее сопротивление вольтметра не задано, следует предположить, что оно настолько велико по сравнению с сопротивлением всех элементов цепи, что силой тока, идущего через вольтметр, можно пренебречь. Тогда сила тока, протекающего через аккумулятор (рис.4.4.), равна заданному значению I1(при разрядке I2).
При зарядке аккумулятора, когда ток I1 направлен так, как показано на рисунке, 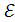 <
< 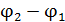 . При разрядке ток I2 направлен в противоположную сторону и
. При разрядке ток I2 направлен в противоположную сторону и 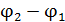 <
< 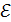 (рис.4.5).
(рис.4.5).
 Следовательно, ЭДС аккумулятора должна удовлетворять условию
Следовательно, ЭДС аккумулятора должна удовлетворять условию
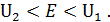
Применяя обобщённый закон Ома к Рисунок 4.5. К задаче 3 участку 1 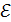 2 для каждого из двух процес-сов, получим два уравнения, содержащих в качестве неизвестных ЭДС и внутреннее сопротивление аккумулятора r.
2 для каждого из двух процес-сов, получим два уравнения, содержащих в качестве неизвестных ЭДС и внутреннее сопротивление аккумулятора r.
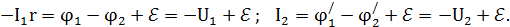
Решая их совместно, получаем:
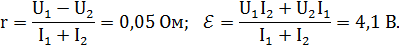
Ответ: r = 0,05 Ом; 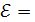 4,1 В.
4,1 В.
Задача 4.Батареи имеют ЭДС 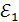 = 110В и
= 110В и 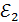 = 220В, сопротивления R1= R2 = 100 м, R3 = 500 Ом. Найти показание амперметра.
= 220В, сопротивления R1= R2 = 100 м, R3 = 500 Ом. Найти показание амперметра.
Решение:Силы токов в разветвленной цепи определим с помощью законов Кирхгофа.
Выберем произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже (рис.4.6). Рассматриваемая схема имеет два узла: А и В. Но составлять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.
При составлении уравнений по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла, - со знаком минус.
Согласно первому правилу Кирхгофа для узла М: 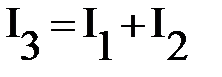 -(1).
-(1).
Недостающие два уравнения получим по второму закону Кирхгофа.  Выберем два независимых контура ABCD и ABMN, для каждого из них укажем направление обхода. Для контура ABMN имеем:
Выберем два независимых контура ABCD и ABMN, для каждого из них укажем направление обхода. Для контура ABMN имеем: 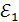
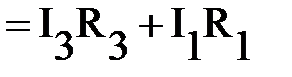 -(2); для контура ABCD:
-(2); для контура ABCD: 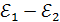
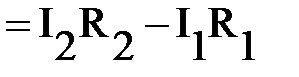 -(3). Из Рисунок 4.6. К задаче 4 уравнения (2) ток
-(3). Из Рисунок 4.6. К задаче 4 уравнения (2) ток
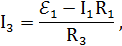
а из уравнения (3) ток
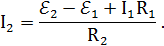
Амперметр покажет ток через сопротивление R1, который из уравнения (1):
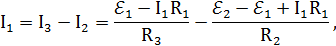
или окончательно
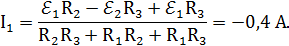
Знак «минус» означает, что мы ошиблись в выборе направления тока I1, т.е. он течёт в противоположном направлении.
Ответ: IA = 0,4 A.
Задача 5.Элемент с ЭДС 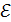 = 2В и внутренним сопротивлением r=0,5Ом замкнут на внешнее сопротивление R. Построить график зависимости от сопротивления R: тока I в цепи, падения потенциала U во внешней цепи, полезной мощности Р и полной мощности Р0. Сопротивление взять в пределах
= 2В и внутренним сопротивлением r=0,5Ом замкнут на внешнее сопротивление R. Построить график зависимости от сопротивления R: тока I в цепи, падения потенциала U во внешней цепи, полезной мощности Р и полной мощности Р0. Сопротивление взять в пределах 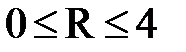 Ом через каждые 0,5 Ом.
Ом через каждые 0,5 Ом.
Решение. Зависимость тока Iв цепи от внешнего сопротивления R выражается законом Ома для полной цепи: 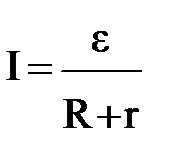 или, с учётом данных задачи,
или, с учётом данных задачи, 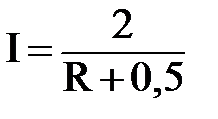 . К.п.д. элемента
. К.п.д. элемента 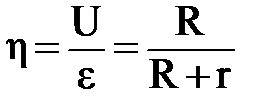 . Тогда
. Тогда 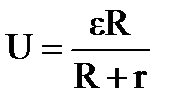 ;
; 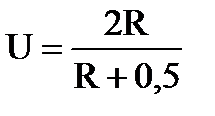 . Зависимости полезной мощности Р и полной мощности Р0 задаются соотношениями:
. Зависимости полезной мощности Р и полной мощности Р0 задаются соотношениями: 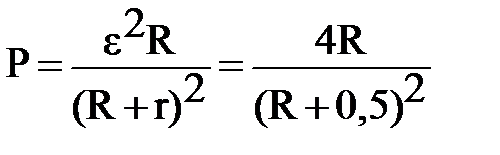 ;
; 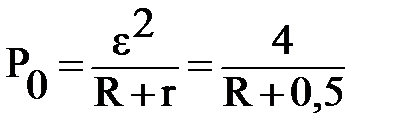 .
.
Для заданного интервала значений R составим таблицу и построим графики.
| R, Ом | 0,5 | 1,5 | 2,5 | 3,5 | |||||
| I, A | 1,33 | 0,8 | 0,67 | 0,57 | 0,5 | 0,44 | |||
| U, B | 1,33 | 1,5 | 1,6 | 1,67 | 1,71 | 1,75 | 1,78 | ||
| P, Вт | 1,78 | 1,5 | 1,28 | 1,11 | 0,98 | 0,88 | 0,79 | ||
| P0, Вт | 2,67 | 1,6 | 1,33 | 1,14 | 0,89 |
Задача 6.Обкладкам конденсатора ёмкости С сообщили разноимённые заряды. Затем обкладки замкнули через сопротивление R. Найти:
а) заряд, прошедший через сопротивление за время τ;
б) количество тепла, выделившееся в сопротивлении за то же время.
Решение. Напряжение на конденсаторе равно напряжению на сопротивлении: q/C=IR.
Поскольку ток течёт за счёт разрядки конденсатора, то 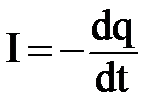 .
.
Получим дифференциальное уравнение, описывающее закон изменения заряда на конденсаторе во времени:
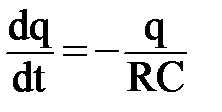 .
.
Решение этого уравнения с учётом начального условия имеет вид:
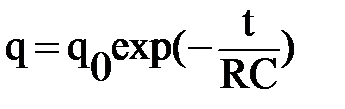 .
.
Отсюда найдём протёкший заряд
q1 = q0 – q(τ) = q0 (1 – exp ( 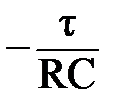 ))
))
Чтобы найти количество тепла, проинтегрируем тепловую мощность по времени:
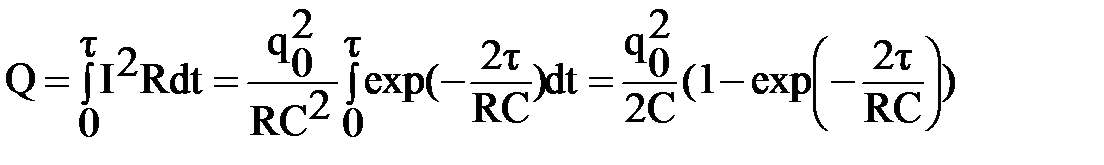
Как и следовало ожидать, выделившееся тепло равно разности энергий конденсатора в при t = 0 и t =τ.
Ответ: q1 = q0 (1 – exp ( 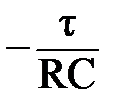 )); Q=
)); Q= 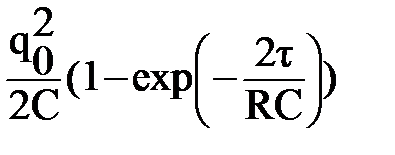 .
.
Вывод: задачи этого параграфа посвящены применению законов постоянного электрического тока: обобщенного закона Ома и правил Кирхгофа, а также закона Джоуля – Ленца.
Дата добавления: 2015-02-13; просмотров: 10703;
