Энергия магнитного поля. Для определения энергии магнитного поля рассмотрим контур, состоящий из источника э.д.с
Для определения энергии магнитного поля рассмотрим контур, состоящий из источника э.д.с. - ε, катушки индуктивности - L и сопротивления - R (рис.3.5). При замыкании цепи ток возрастает от 0 до I, и, следовательно, возникает э.д.с. самоиндукции εis, направленная против э.д.с. ε, возбуждающей ток. При размыкании цепи сила тока уменьшается от I до 0, что вызывает появление э.д.с. самоиндукции εis того же направления, что и направление внешней ε. Можно предположить, что на увеличение тока в контуре затрачивается дополнительная работа, идущая на создание энергии магнитного поля. При снижении тока эта энергия выделяется в виде дополнительного джоуль-ленцева тепла.
| ε |
| R |
| L |
| Рисунок 3.5 - К определению энергии магнитного поля |
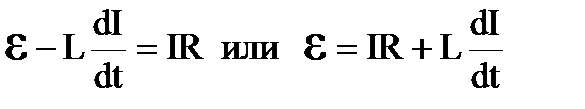 .
.
Подсчитаем работу, совершаемую источником э.д.с. за время dt. Для этого воспользуемся формулой для мощности тока N=dA/dt=Iε. Объединив два последних выражения, получим
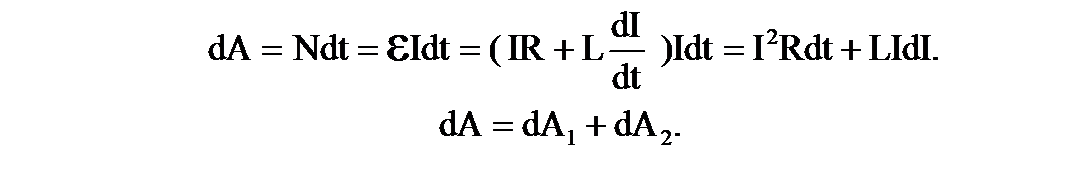
Первое слагаемое dA1 = I2Rdt – это работа, расходуемая на нагревание проводника, т.е. тепло, выделяемое в проводнике за время dt. Второе слагаемое dA2 = LIdI – работа, обусловленная индукционными явлениями. Данная дополнительная работа, затрачиваемая на увеличение силы тока в контуре от 0 до I, находится как интеграл:
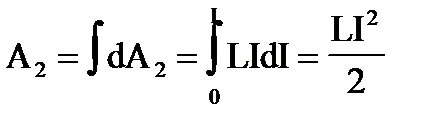 .
.
Полученная работа LI2/2 представляет собой собственную энергию тока в контуре с индуктивностью L.
Увеличение силы тока в проводнике вызывает соответствующее усиление его магнитного поля, которое, подобно электрическому, обладает энергией. Найденная нами собственная энергия тока в контуре есть не что иное, как энергия Wm магнитного поля этого контура с током. Эта энергия запасена в магнитном поле катушки так же, как энергия электрического поля запасена в заряженном конденсаторе. Таким образом,
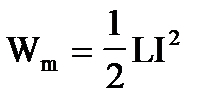 .
.
В этой формуле магнитная энергия выражена через параметры, характеризующие контур с током – силу тока I и индуктивность катушки L. Ту же энергию Wm можно выразить через параметры, характеризующие само магнитное поле, а именно, напряженность поля 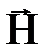 , магнитную индукцию
, магнитную индукцию 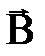 и объем занимаемого полем пространства V. Для этого найдем энергию магнитного поля соленоида. Воспользуемся полученным нами ранее выражением для индуктивности соленоида:
и объем занимаемого полем пространства V. Для этого найдем энергию магнитного поля соленоида. Воспользуемся полученным нами ранее выражением для индуктивности соленоида:
L = n2μμ0V.
Индукция магнитного поля соленоида В = nμμ0I, откуда I = B/nμμ0. Таким образом, искомая энергия:
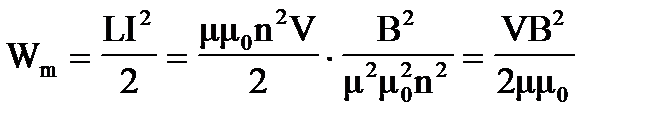 .
.
Так как В= μμ0Н, то 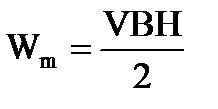 .
.
Если магнитное поле однородно, его энергия распределена равномерно по всему объему поля с некоторой объемной плотностью wm:
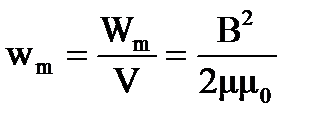 .
.
Последнее соотношение можно переписать в трех эквивалентных формах:
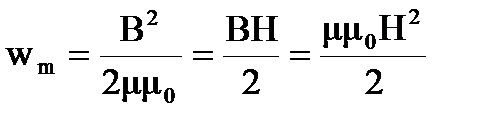 .
.
Если магнитное поле неоднородно, его объемная плотность меняется от точки к точке. Зная wm в каждой точке, можно найти энергию поля, заключенную в некотором объеме V. Для этого нужно вычислить интеграл:
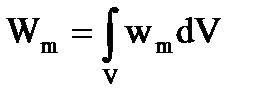 .
.
Контрольные вопросы первого уровня
1. Что называется магнитным потоком? Чему равен магнитный поток сквозь произвольную замкнутую поверхность?
2. В чем заключается суть опытов Фарадея? Приведите примеры.
3. Сформулировать закон электромагнитной индукции и закон Ленца.
4. Выведите закон электромагнитной индукции на основе закона сохранения энергии.
5. Что называется явлением самоиндукции?
6. Что называется индуктивностью? От чего зависит индуктивность? Каковы единицы измерения индуктивности?
7. Чему равна индуктивность соленоида?
8. Чему равна ЭДС самоиндукции? Как направлен ток самоиндукции при убывании тока в катушке?
9. Что называется явлением взаимной индукции? От чего зависит коэффициент взаимной индукции?
10. Чему равна энергия магнитного поля? Чему равна объемная плотность энергии магнитного поля?
Методические указания по решению задач
При решении задач на закон электромагнитной индукции следует придерживаться следующей схемы.
1. Проанализировать условие задачи, выявить причины изменения потока вектора магнитной индукции. Поток вектора 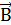 изменяется за счет того, что со временем меняется либо магнитное поле, либо площадь, ограниченная контуром, либо угол между вектором
изменяется за счет того, что со временем меняется либо магнитное поле, либо площадь, ограниченная контуром, либо угол между вектором 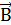 и нормалью к контуру.
и нормалью к контуру.
2. Затем выражение для потока вектора магнитной индукции нужно представить в развернутом виде и записать изменение этого потока за время 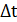 .
.
3. Записать выражение для закона электромагнитной индукции и, если этого требует условие задачи, дополнительные условия. Решить полученную систему уравнений относительно искомой величины.
Цель: Расчет электродвижущей силы индукции и силы тока индукции.
Дата добавления: 2015-02-13; просмотров: 1406;
