Атом водорода в квантовой механике

Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не"¹", двукратно ионизованного лития Li^{+ +} и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z= 1),

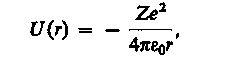
где r— расстояние между электроном и ядром. Графически функция U(r)изображена жирной кривой на рис. 302. U(r) с уменьшением г (при приближении электрона к ядру) неограниченно убывает.

Состояние электрона в атоме водорода описывается волновой функцией Y, удовлетворяющей стационарному уравнению Шредингера (217.5), учитывающему значение (223.1):

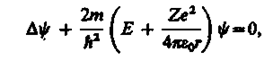(223.2)

где m— масса электрона, Е— полная энергия электрона в атоме. Так как поле, в котором движется электрон, является центрально-симметричным, то для решения уравнения (223.2) обычно используют сферическую систему координат: r, q, j. Не вдаваясь в математическое решение этой задачи, ограничимся рассмотрением важнейших результатов, которые из него следуют, пояснив их физический смысл.

1. Энергия. В теории дифференциальных уравнении доказывается, что уравнения типа (223.2) имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции Y, только при собственных значениях энергии

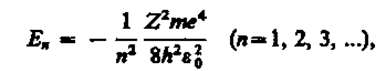(223.3)

т. е. для дискретного набора отрицательных значений энергии.

Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими «стенками» (см. § 220) и гармонического осциллятора (см. § 222), решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е₁, Е₂, Е₃,...показаны на рис. 302 в виде горизонтальных прямых. Самый нижний уровень E_l,отвечающий минимальной возможной энергии, — основной, все остальные (E_n > E₁,n = 2, 3, ...) — возбужденные (см. § 212). При Е < 0движение электрона является связанным — он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа nэнергетические уровни располагаются теснее и при n = ¥ E_¥ = 0. При Е > 0 движение электрона является свободным; область непрерывного спектра Е > 0(заштрихована на рис. 302) соответствует ионизованному атому. Энергия ионизации атома водорода равна

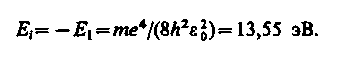
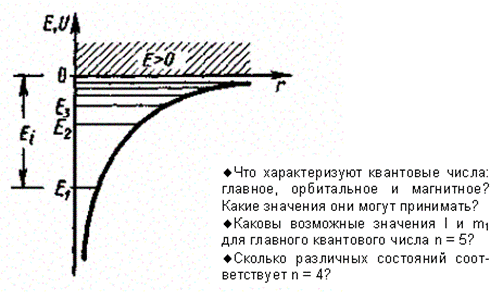
Рис. 302

Выражение (223.3) совпадает с формулой (212.3), полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следствием самой теории, вытекают непосредственно из решения уравнения Шредингера.

2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции Y (r, в, <р), определяемые тремя квантовыми числами: главным л, орбитальным / и магнитным /и/.

Главное квантовое число л, согласно (223.3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с единицы:

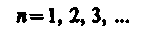
Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

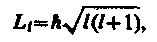(223.4)

где l — орбитальное квантовое число, которое при заданном л принимает значения

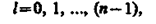(223.5)

т. е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L_l момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_lx на направление z внешнего магнитного поля принимает квантованные значения, кратные n:

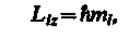(223.6)

где m_l — магнитное квантовое число, которое при заданном l может принимать значения

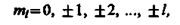(223.7)

т. е. всего 2l+1 значений. Таким образом, магнитное квантовое число m_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации.

Наличие квантового числа m_l должно привести в магнитном поле к расщеплению уровня с главным квантовым числом nна 2l+1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщепление энергетических уровней в магнитном поле было обнаружено в 1896 г. голландским физиком П. Зееманом (1865—1945) и получило название эффекта Зеемана. Расщепление уровней энергии во внешнем электрическом поле, тоже доказанное экспериментально, называется эффектом Штарка*.

Хотя энергия электрона (223.3) и зависит только от главного квантового числа n, но каждому собственному значению Е_n(кроме E₁) соответствует несколько собственных функций Y_nlml, отличающихся значениями l и m_l. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном n орбитальное квантовое число l может изменяться от 0 до n - 1 (см. (223.5)), а каждому значению l соответствует 2l+1 различных значений /и/ (223.7), то число различных состояний, соответствующих данному n, равно

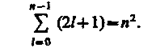(223.8)

Квантовые числа и их значения являются следствием решений уравнений Шредингера и условий однозначности, непрерывности и конечности, налагаемых на волновую функцию Y. Кроме того, так как при движении электрона в атоме существенны волновые свойства электрона, то квантовал механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в раз личных точках объема атома. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l = 0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l = 1 — p-состоянием, l = 2 — d-состоянием, l = 3 — f-состоянием и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в со стояниях с n = 2 и l = 0 и 1 обозначаются соответственно символами 2s и 2р.

На рис. 303 для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при n=1 и n=2, определяемое |Y_nlml |². Как видно из рисунка, оно зависит от n, l и m_l. Так, при l = 0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически-симметрична), а для остальных состояний в центре равна нулю и зависит от направления.

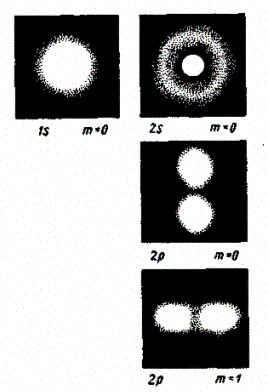
Рис. 303

3. Спектр. Квантовые числа n, l и m_l позволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора (см. рис. 294).

В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Теоретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа D l удовлетворяет условию

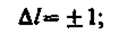(223.9)

2) изменение магнитного квантового числа Am/ удовлетворяет условию

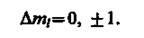
В оптических спектрах указанные правила отбора в основном выполняются. Однако в принципе могут наблюдаться и слабые «запрещенные» линии, например возникающие при переходах с Dl = 2. Появление этих линий объясняется тем, что строгая теория, запрещая дипольные переходы, разрешает переходы, соответствующие излучению более сложных систем зарядов, например квадруполей. Вероятность же квадрупольных переходов (переходы с Dl= 2) во много раз меньше вероятности дипольных переходов, поэтому «запрещенные» линии и являются слабыми.

Учитывая число возможных состояний, соответствующих данному л, и правило отбора (223.9), рассмотрим спектральные линии атома водорода (рис. 304): серии Лаймана соответствуют переходы

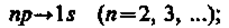
серии Бальмера —

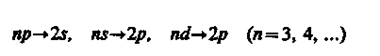
и т.д.

Переход электрона из основного состояния в возбужденное обусловлен увеличением энергии атома и может происходить только при сообщении атому энергии извне, например за счет поглощения атомом фотона. Так как поглощающий атом находится обычно в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 1s®np (n=2, 3, ...), что находится в полном согласии с опытом.

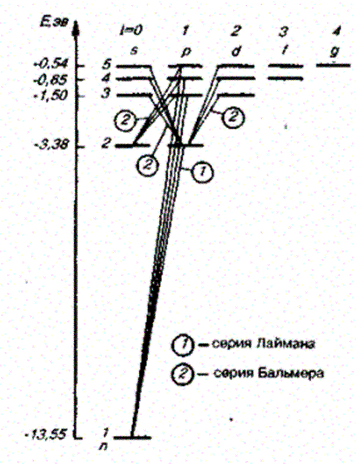
Рис. 304