В квантовой механике

Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории (см. § 142). Пружинный, физический и математический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора (см. (141.5)) равна

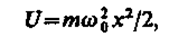(222.1)

где w₀ — собственная частота колебаний осциллятора, m— масса частицы. Зависимость (222.1) имеет вид параболы (рис. 300), т. е. «потенциальная яма» в данном случае является параболической.

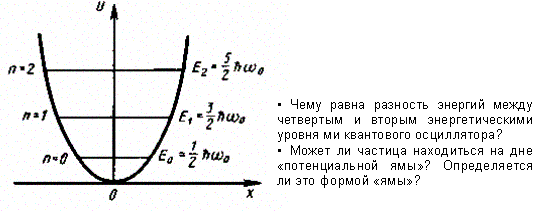
Рис. 300

Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е(см. рис. 16). В точках с координатами ±х_max полная энергия Еравна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (-х_max, + х_max). Такой выход означал бы, что ее потенциальная энергия больше полной, что абсурдно, так как приводит к выводу, что кинетическая энергия отрицательна. Таким образом, классический осциллятор находится в «потенциальной яме» с координатами —

- х_max £ x £ х_max «без права выхода» из нее.

Гармонический осциллятор в квантовой механике — квантовый осциллятор — описывается уравнением Шредингера (217.5), учитывающим выражение (222.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида

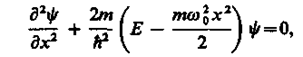(222.2)

где Е — полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что уравнение (222.2) решается только при собственных значениях энергии

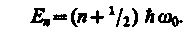(222.3)

Формула (222.3) показывает, что энергия квантового осциллятора может иметь лишь декретом значения, т. е. квантуется. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками» (см. § 220), минимальным значением энергии E₀ = 1/2ℏw₀. Существование минимальной энергии — она называется энергией нулевых колебаний — является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.

Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых колебаний квантового осциллятора противоречит выводам классической теории, согласно которой наименьшая энергия, которую может иметь осциллятор, равна нулю (соответствует покоящейся в положении равновесия частице). Например, классическая физика приводит к выводу, что при Т=0энергия колебательного движения атомов кристалла должна обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное колебаниями атомов. Однако эксперимент показывает, что интенсивность рассеяния света при понижении температуры не равна нулю, а стремится к некоторому предельному значению, указывающему на то, что при T®0 колебания атомов в кристалле не прекращаются. Это является подтверждением наличия нулевых колебаний.

Из формулы (222.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (рис. 300), а именно расстояние между соседними энергетическими уровнями равно ℏw₀, причем минимальное значение энергии E₀ = 1/2ℏw₀.

Строгое решение задачи о квантовом осцилляторе приводит еще к одному значительному отличию от классического рассмотрения. Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области |х| < х_max (см. рис. 16), в то время как с классической точки зрения она не может выйти за пределы области (- х_max, + х_max). Таким образом, имеется отличная от нуля вероятность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без его вывода) демонстрируется на рис. 301, где приводится квантовая плотность вероятности w обнаружения осциллятора для состояния n = 1.

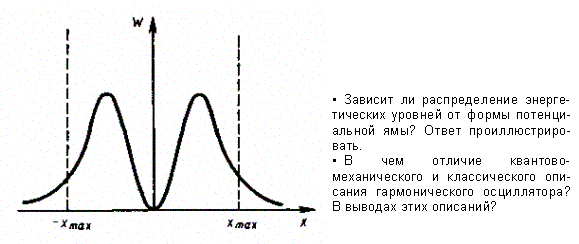
Рис. 301

Из рисунка следует, что для квантового осциллятора действительно плотность вероятности wимеет конечные значения за пределами классически дозволенной области |x| ³ х_max т. е. имеется конечная (но небольшая) вероятность обнаружить частицу в области за пределами «потенциальной ямы». Существование отличных от нуля значений wза пределами «потенциальной ямы» объясняется возможностью прохождения микрочастиц сквозь потенциальный барьер (см. § 221).

Задачи

28.1. Свободная частица движется со скоростью u. Доказать, что выполняется соотношение v_фазu = c².

28.2. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 1% от ее числового значения, определить неопределенность координаты электрона. Применительно ли в данном случае для электрона понятие траектории? [Dх=33 нм; нет]

28.3. Y-Функция некоторой частицы имеет вид 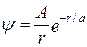, где г — расстояние этой частицы от силового центра, а — постоянная. Определить среднее расстояние árñ частицы от силового центра. [árñ=p/2]

28.4. Записать уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода.

28.5. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной lс бесконечно высокими «стенками». Определить вероятность Wобнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n=2).Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. [W=0,195]

28.6. Прямоугольный потенциальный барьер имеет ширину 0,1 нм. Определить в электрон-вольтах разность энергий U - E,при которой вероятность прохождения электрона сквозь барьер составит 0,99. [0,1 мэВ]