Процесс

Адиабатическим называется процесс, при котором отсутствует теплообмен («52=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики (dQ = dU + dA)для адиабатического процесса следует, что

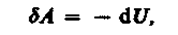(55.1)

т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражения (52.1) и (53.4), для произвольной массы газа перепишем уравнение (55.1) в виде

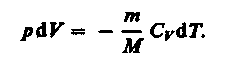(55.2)

Продифференцировав уравнение состояния для идеального газа 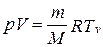, получим

(55.3)

Исключим из (55.2) и (55.3) температуру Т:

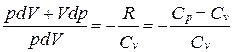
Разделив переменные и учитывая, что С_р/С_v = g (см. (53.8)), найдем

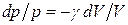
Интегрируя это уравнение в пределах от p₁ до р₂и соответственно от V₁до V₂, а затем потенцируя, придем к выражению

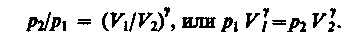
Так как состояния 1 и 2 выбраны произвольно, то можно записать

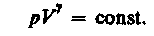(55.4)

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или p, Т исключим из (55.4) с помощью уравнения Клапейрона — Менделеева

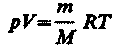
соответственно давление или объем:

(55.5) (55.6)

Выражения (55.4) — (55.6) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина (см. (53.8) и (53.2))

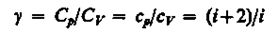(55.7)

называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, I = 3, g=1,67. Для двухатомных газов (Н₂, N₂, O₂ и др.) I = 5, g= 1,4. Значения у, вычисленные по формуле (55.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, Vизображается гиперболой (рис. 83). На рисунке видно, что адиабата (pV⁷ = const) более круга, чем изотерма (pV = const). Это объясняется тем, что при адиабатическом сжатии 1—3увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

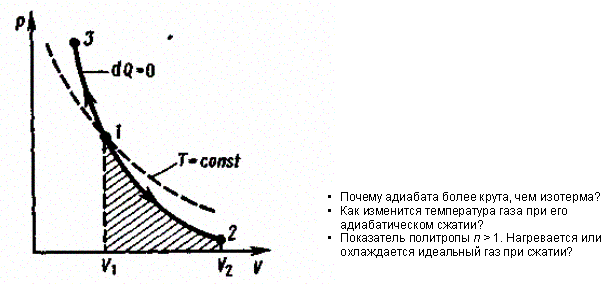
Рис. 83

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение (55.1) в виде

Если газ адиабатически расширяется от объема V\ до V₂, то его температура уменьшается от T₁до T₂и работа расширения идеального газа

(55.8)

Применяя те же приемы, что и при выводе формулы (55.5), выражение (55.8) для работы при адиабатическом расширении можно преобразовать к виду

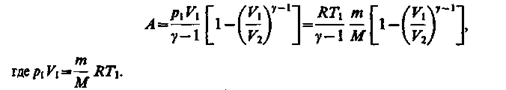
Работа, совершаемая газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 83), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_V и С_р, в изотермическом процессе (dT = 0)теплоемкость равна ± ¥, в адиабатическом (dQ = 0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется полнтропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (С = const) можно вывести уравнение политропы:

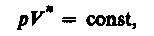(55.9)

где n=(C—C_p)/(C—C_V)— показатель политропы. Очевидно, что при С=0, n = 0,из (55.9) получается уравнение адиабаты; при С = ¥, n = 1 —уравнение изотермы; при С = С_p, n = 0 — уравнение изобары, при С = С_V, n = ± ¥ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.