Визначення прогинів залізобетонних елементів, що згинаються
Однією з головних деформативних характеристик залізобетонних елементів, що згинаються, є величина прогину f. Залежно від цієї величини визначається ступінь придатності конструкції до нормальної експлуатації, тобто встановлюється можливість конструкції задовольняти заданим технологічним вимогам (підкранові балки, плити перекриття для високоточних верстатів, пролітні будівлі мостів і т.п.), а також естетичним вимогам для конструктивних елементів цивільних і промислових будівель.
Значення гранично припустимих прогинів наведені в табл.5.1 (згідно із СНіП 2.03.01–84* [7]).
Теоретичною базою для визначення величини прогинів є класичний апарат будівельної механіки, що базується на визначенні прогинів за допомогою інтеграла Мора:
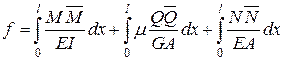 . .
| (5.16) |
Даний інтеграл для найпростіших випадків спрощується і зводиться для елементів, що згинаються, до вигляду
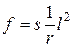 , ,
| (5.17) |
де s – параметр виду силового впливу на елемент; 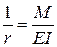 – кривизна залізобетонного елементу;
– кривизна залізобетонного елементу;
l – розрахунковий проліт елемента, для якого визначається прогин.
Основну складність в обчисленні прогину за формулою (5.17) становить визначення кривизни 1/r. Для обчислення її потрібно враховувати відсутність чи наявність тріщин у залізобетонному елементі, характер і вид навантаження, тривалість дії навантажень, геометричні характеристики перерізу і цілий ряд додаткових параметрів.
На ділянках, де не утворюються тріщини, нормальні до поздовжньої осі елемента, повна величина кривизни згинаних, позацентрово стиснутих і позацентрово розтягнутих елементів визначається за формулою
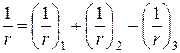 , ,
| (5.18) |
де 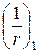 і
і 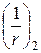 – кривизни відповідно від нетривалої і тривалої дії навантажень. Зусилля попереднього обтиснення P в цих кривизнах не враховують.
– кривизни відповідно від нетривалої і тривалої дії навантажень. Зусилля попереднього обтиснення P в цих кривизнах не враховують.
Значення даних кривизн можна визначити за формулою
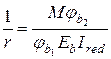 , ,
| (5.19) |
тут М – момент від відповідного зовнішнього навантаження (короткочасної чи тривалої дії) щодо осі, нормальної до площини дії згинаючого моменту і минаючої через центр ваги приведеного перерізу;
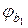 – коефіцієнт, що враховує вплив короткочасної повзучості бетону; для важкого, дрібнозернистого, легкого на щільному заповнювачі і чарункового бетонів
– коефіцієнт, що враховує вплив короткочасної повзучості бетону; для важкого, дрібнозернистого, легкого на щільному заповнювачі і чарункового бетонів 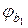 =0,85; для легкого на пористому заповнювачі
=0,85; для легкого на пористому заповнювачі 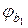 =0,70;
=0,70;
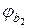 – коефіцієнт, що враховує вплив тривалої повзучості і приймається у відповідності до табл.5.2.
– коефіцієнт, що враховує вплив тривалої повзучості і приймається у відповідності до табл.5.2.
Таблиця 5.1 – Гранично допустимі прогини елементів
| № п/п | Елементи конструкцій | Гранично допустимі прогини f |
| 1. | Підкранові балки при кранах: електричних ручних | l / 600 l / 500 |
| 2. | Елементи плоского перекриття (балки, плити) і елементи покриття при прольотах l у м: l < 6 6< l £ 7,5 l > 7,5 | l / 200 l / 250 але не більш 3 см l / 250 |
| 3. | Перекриття з ребристою стелею й елементи сходів при прольотах l у м: l < 5 5 < l £ 10 l > 10 | l / 200 2,5 см l / 400 |
| 4. | Навісні стінові панелі (із площини) при прольотах l у м: l < 6 6 < l £ 7,5 l > 7,5 | l / 200 3 см l / 250 |
Таблиця 5.2
| Тривалість дії навантаження | Коефіцієнт для конструкцій з важкого, легкого, поризованого, чарункового, дрібнозернистого (група А) при класі бетону | ||
| нижче B30 | 30 £ B £ 50 | вище B50 | |
| 1.Нетривале (короткочасна дія) | |||
| 2.Тривала дія при вологості повітря W, % а) нижче 40 (дуже сухо) б) 40 £ W £ 60 в) 60 £ W £ 80 г) 80 £ W £ 100 | 4,0 3,5 3,0 2,5 | 3,4 3,0 2,6 2,2 | 2,9 2,5 2,0 1,9 |
Вологість повітря навколишнього середовища визначається як середня відносна вологість зовнішнього повітря найбільш жаркого місяця залежно від району будівництва згідно із СНіП 2.01.01-82 чи як відносна вологість внутрішнього повітря приміщень опалювальних будинків.
Для дрібнозернистих бетонів (групи Б и В) 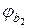 необхідно коригувати відповідно коефіцієнтами 1,15 і 0,8.
необхідно коригувати відповідно коефіцієнтами 1,15 і 0,8.
Значення кривизни 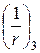 , що характеризує вигин елемента від дії зусилля попереднього обтиснення P, визначається залежністю
, що характеризує вигин елемента від дії зусилля попереднього обтиснення P, визначається залежністю
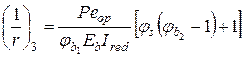 , ,
| (5.20) |
де Р – зусилля попереднього обтиснення з урахуванням тільки перших втрат;
js – коефіцієнт, що враховує вплив тривалої повзучості й усадки бетону на величину зусилля попереднього обтиснення
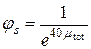 , ,
| (5.21) |
де μtot – коефіцієнт повного армування, прийнятий рівним відношенню площ перерізу арматури стиснутої (S') і розтягнутої (S) до площі перерізу бетону.
На ділянках, де в розтягнутій зоні утворюються нормальні до поздовжньої осі елемента тріщини, кривизна згинаних, позацентрово стиснутих, а також позацентрово розтягнутих при e0,tot ³ 0,8h0 елементів прямокутного, таврового і двотаврового чи коробчатого перерізів повинна визначатися за формулою
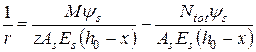 , ,
| (5.22) |
де М – момент зовнішніх сил, включаючи силу P, щодо центру ваги розтягнутої арматури S;
z – відстань від центру ваги площі перерізу арматури S до точки прикладання рівнодіючої зусиль у стиснутій зоні над тріщиною. Величину z обчислюють за формулою
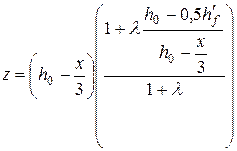
| (5.23) |
(z £ 0,97es,tot для позацентрово стиснутих елементів).
У цій формулі
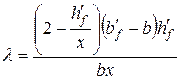 , ,
| (5.24) |
а величина х повинна визначатися за формулою
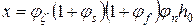 , ,
| (5.25) |
де
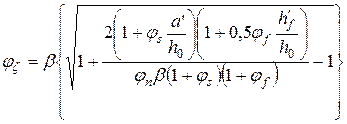 . .
| (5.26) |
У формулі (5.26) прийняті такі позначення:
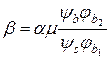 ;
; 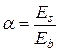 ;
; 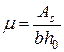 ;
; 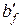 і
і 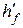 – ширина і висота стиснутої полиці в таврових перерізах; для прямокутних перерізів за формулою (5.24)
– ширина і висота стиснутої полиці в таврових перерізах; для прямокутних перерізів за формулою (5.24) 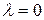 ;
; 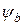 – коефіцієнт, що враховує нерівномірність розподілу деформацій крайнього стиснутого волокна бетону на довжині ділянки з тріщинами, прийнятий рівним 0,9 для бетонів класів вище В > 7,5; для легких бетонів і класів В < 7,5
– коефіцієнт, що враховує нерівномірність розподілу деформацій крайнього стиснутого волокна бетону на довжині ділянки з тріщинами, прийнятий рівним 0,9 для бетонів класів вище В > 7,5; для легких бетонів і класів В < 7,5 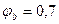 ;
;
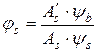 , ,
| (5.27) |
де 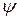 s – коефіцієнт, що враховує роботу розтягнутого бетону на ділянках з тріщинами й обчислений за формулою
s – коефіцієнт, що враховує роботу розтягнутого бетону на ділянках з тріщинами й обчислений за формулою
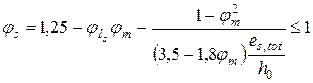 ; ;
| (5.28) |
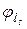 – для нетривалої дії навантажень дорівнює 1, для тривалої дії дорівнює 0,8.
– для нетривалої дії навантажень дорівнює 1, для тривалої дії дорівнює 0,8.
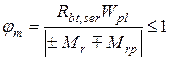 , ,
| (5.29) |
Мr – момент зовнішніх сил щодо ядрової точки, найбільш віддаленої від розтягнутої зони; Mpr – момент зусилля попереднього обтиснення Р щодо тієї ж ядрової точки. Додатніми вважаються ті моменти, що викликають розтягання в розтягнутій арматурі S; Wpl – пружно-пластичний момент опору, що може бути прийнятий для прямокутних і таврових перерізів з полицею у стиснутій зоні Wpl = 1,75Wred;
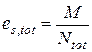 , ,
| (5.30) |
де М – момент зовнішніх сил відповідно до формули (5.22); Ntot – рівнодіюча поздовжньої сили N і зусилля попереднього обтиснення Р (при позацентровому розтяганні сила N приймається зі знаком “мінус”).
Коефіцієнти 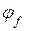 й
й  у формулах (5.25) і (5.26) обчислюють за залежностями
у формулах (5.25) і (5.26) обчислюють за залежностями
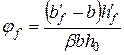 , ,
| (5.31) |
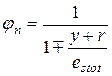 . .
| (5.32) |
Параметри 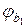 і
і 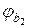 , що входять до формули для
, що входять до формули для 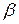 , слід приймати за рекомендаціями для формули (5.19).
, слід приймати за рекомендаціями для формули (5.19).
У формулі (5.32) y – відстань від центру ваги приведеного перерізу до центру ваги площі перерізу розтягнутої арматури S (основної робочої); r – відстань від центру ваги приведеного перерізу до ядрової точки: див. формулу (5.7). У формулі (5.32) верхній знак приймається при стискаючому зусиллі N.
Для елементів, що згинаються, без попереднього напруження арматури у формулі (5.28) останній доданок правої частини можна приймати рівним нулю.
Рекомендується для визначення загальної кривизни елементів із тріщинами починати розрахунок з обчислення коефіцієнта 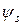 , потім визначаються коефіцієнти
, потім визначаються коефіцієнти 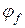 ,
,  та всі інші параметри.
та всі інші параметри.
Повна кривизна 1/r для ділянки з тріщинами в розтягнутій зоні повинна обчислюватися в такій послідовності:
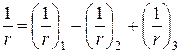 , ,
| (5.33) |
де 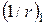 – кривизна від нетривалої дії всього навантаження;
– кривизна від нетривалої дії всього навантаження;
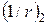 – кривизна від нетривалої дії тільки постійних і тривалих навантажень;
– кривизна від нетривалої дії тільки постійних і тривалих навантажень;
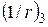 – кривизна від тривалої дії постійних і тривалих навантажень.
– кривизна від тривалої дії постійних і тривалих навантажень.
Кривизни 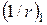 і
і 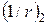 , обчислюють при значеннях
, обчислюють при значеннях 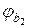 і
і 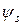 та інших параметрів, що відповідають нетривалій дії навантажень;
та інших параметрів, що відповідають нетривалій дії навантажень; 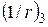 – при
– при 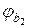 й
й 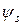 та інших параметрів, що відповідають тривалій дії навантажень.
та інших параметрів, що відповідають тривалій дії навантажень.
Значення величини s, що входить у формулу (5.17), можуть бути прийняті такі: для рівномірно розподіленого навантаження і вільно опертої балки s = 5/48, при зосередженому навантаженні посередині прольоту s = 1/12, при наявності зосереджених моментів по кінцях балки s = 1/8.
В останніх нормативних документах [12, 13] рекомендується визначати крім прогинів залізобетонних конструкцій ще їхні поздовжні деформації у відносному значенні. Так, на ділянках, де утворяться тріщини, повна величина відносних деформацій (подовження чи укорочення) у поздовжньому напрямку визначається за формулою
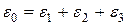 , ,
| (5.34) |
де e1 і e2 – відносні деформації від навантажень нетривалої і тривалої дії;
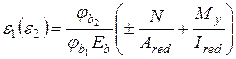 ; ;
| (5.35) |
e3 – відносні деформації в напрямку поздовжньої осі від зусилля попереднього обтиснення P з урахуванням тільки перших втрат:
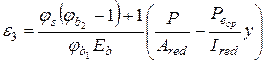 . .
| (5.36) |
Значення параметрів, що входять у формули (5.35), (5.36), можна визначати за вищенаведеними формулами.
На ділянках, де утворюються тріщини, відносні деформації можуть обчислюватися за формулою
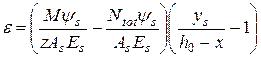 , ,
| (5.37) |
де ys – відстань від розглянутого волокна до арматури S , інші параметри наведені вище.
Укорочення чи подовження на рівні розглянутого волокна повинне визначатися за формулою (при розбивці всієї довжини на n ділянок)
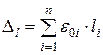 , ,
| (5.38) |
де e0і – відносні поздовжні деформації в перерізі, розташованому посередині ділянки довжиною li.
Для кутів поворотів залізобетонних елементів існуючі нормативні документи поки що не дають певних математичних залежностей.
Контрольні запитання для самоперевірки
1. Що містить у собі розрахунок залізобетонних конструкцій за II групою граничних станів?
2. Які існують категорії тріщиностійкості залізобетонних елементів?
3. Як записується умова тріщиностійкості для центрально розтягнутих елементів і для тих, що згинаються?
4. Як визначається ширина розкриття тріщин, від чого вона залежить?
5. Як виконується розрахунок на закриття тріщин?
6. Прогини, що допускаються, для окремих залізобетонних конструкцій.
7. У чому полягає методика обчислення прогинів для залізобетонних конструкцій без тріщин?
8. У чому полягає методика обчислення прогинів для залізобетонних конструкцій з тріщинами?
9. Охарактеризуйте параметр ys і його призначення.
10.Як враховується в розрахунках прогинів вплив навантажень тривалої дії?
11.Як впливає на значення прогинів попереднє напруження арматури?
Дата добавления: 2015-02-13; просмотров: 3588;
