Теорема про активний двополюсник.
Струм у вітці а, б електричного кола не зміниться, якщо активний двопо-люсник(Рис. 42, а), до якого під’єднана вітка, замінити еквівалентним джере-лом, ЕРС якого дорівнює напрузі розриву на полюсах активного двопо-люсника, а внутрішній опір дорівнює вхідному опору відносно полюсів а, б пасивного двополюсника, одержаного із даного активного двополюсника вида-ленням джерел енергії (Рис. 42, б).
Доведемо теорему.

1. Від’єднуємо опір навантаження 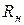 (режим розриву - р) (Рис. 43, а) і виз-начаємо напругу розриву
(режим розриву - р) (Рис. 43, а) і виз-начаємо напругу розриву  активного двополюсника, яка дорівнює еквіва-лентній ЕРС
активного двополюсника, яка дорівнює еквіва-лентній ЕРС  двополюсника. Якщо послідовно з навантаженням ввімкнути зустрічно дві однакові ЕРС
двополюсника. Якщо послідовно з навантаженням ввімкнути зустрічно дві однакові ЕРС 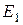 і
і 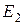 (Рис. 43, б), що дорівнюють напрузі розри-ву, струм у вітці не зміниться.
(Рис. 43, б), що дорівнюють напрузі розри-ву, струм у вітці не зміниться.
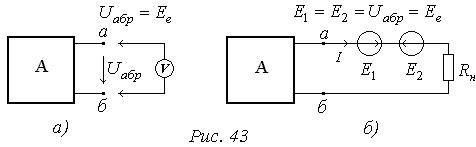
2. Розраховуємо коло (Рис. 43, б)методом накладання, для цього розгляне-мо два часткові кола. У перше коло входять всі джерела активного двопо-люсника і ЕРСЕ2 (Рис. 44, а), у друге - пасивний двополюсник (без джерел енергії) і ЕРС Е1 (Рис. 44, б).

Струм  , тому що при розриві
, тому що при розриві  , отже увімкнення резистора
, отже увімкнення резистора 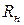 не викликає появу струму. Оскільки
не викликає появу струму. Оскільки 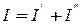 , то струм
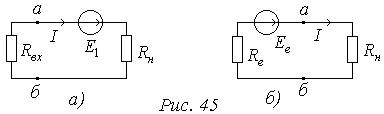
, то струм 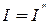 , тобто дорівнює струму у другому частковому колі (Рис.44, б). Двополюсник можна замінити вхідним еквівалентним опором, при цьому коло спроститься (Рис.45, а). ЕРС
, тобто дорівнює струму у другому частковому колі (Рис.44, б). Двополюсник можна замінити вхідним еквівалентним опором, при цьому коло спроститься (Рис.45, а). ЕРС 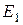 є ЕРС еквівалентного генератора
є ЕРС еквівалентного генератора  , а вхідний опір
, а вхідний опір 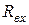 -внутрішнім опором еквівалентного генератора
-внутрішнім опором еквівалентного генератора 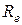 (Рис. 45, б).
(Рис. 45, б).
Струм у вітці 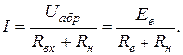
Алгоритм розрахунку електричного кола методом еквівалентного генератора.
1. Від’єднуємо вітку, в якій визначається струм.
2. Будь-яким із відомих методів розрахувуємо коло, що залишилося (режим-розриву активного двополюсника) і визначаємо напругу між точками а, б, до яких була під’єднана вітка.
між точками а, б, до яких була під’єднана вітка.
3. Видаляємо із кола джерела енергії, замінивши їх внутрішніми опорами, виз-начаємо вхідний опір 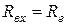 відносно точок а, б.
відносно точок а, б.
4. Визначаємо струм у вітці за формулою: 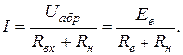
5. Якщо у вітці, струм якої розраховуємо, є джерело ЕРС (Рис. 46, а), то розра-хунок ведеться за формулою:


6. Якщо у вітці, струм якої розраховується, відсутні опір і ЕРС (коротке зами-кання вітки) (Рис. 46, б) то:
 ,звідки:
,звідки: 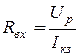 .
.
Приклад 5. Визначити струм  у колі так званого моста (Рис.П5, а).
у колі так званого моста (Рис.П5, а).
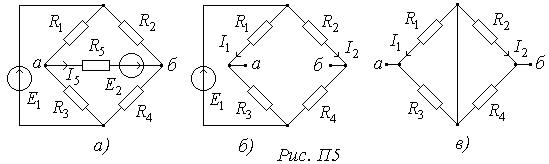
1. Від’єднуємо вітку зі струмом  (Рис. П5, б).
(Рис. П5, б).
2. Розраховуємо коло, що залишилося (режим розриву активного двопо-люсника) і визначаємо напругу  між точками а, б, до яких була під’єднана вітка.
між точками а, б, до яких була під’єднана вітка.
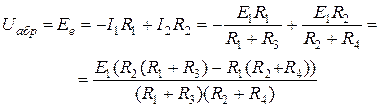
Після спрощення виразу одержуємо: 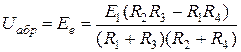 .
.
Очевидно, якщо  то
то  , (мостова схема врівноважена).
, (мостова схема врівноважена).
3. Видаляємо із схеми 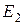 , замінивши її внутрішнім опором (закоротка), визначаємо вхідний опір
, замінивши її внутрішнім опором (закоротка), визначаємо вхідний опір 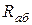 відносно точок а, б (Рис. П5, в). Опори
відносно точок а, б (Рис. П5, в). Опори 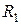 і
і  ,
, 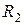 і
і  з’єднані паралельно, а між собою - послідовно.
з’єднані паралельно, а між собою - послідовно.
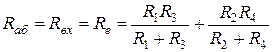
4. Струм  визначається за формулою:
визначається за формулою: 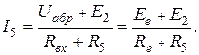
Приклад 6.
І) Розрахувати струм у вітці з ЕРС 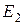 (Рис. П6, а).
(Рис. П6, а).
ІІ) Визначити, якою повинна бути ЕРС 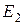 , щоб струм
, щоб струм 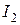 при тому ж
при тому ж
значенні змінив свій напрям.
ІІІ) Знайти залежність між струмом 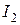 у другій вітці і опором
у другій вітці і опором  у
у
четвертій вітці при незмінних всіх інших параметрах.
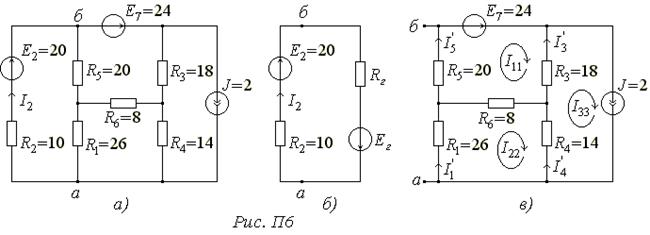 I. Розраховуємо струм
I. Розраховуємо струм 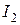 методом еквівалентного генератора.
методом еквівалентного генератора.
1. На Рис. П6, в відімкнена друга вітка. Коло, що залишилося, розраховуємо методом контурних струмів, які показані на схемі. Струм 
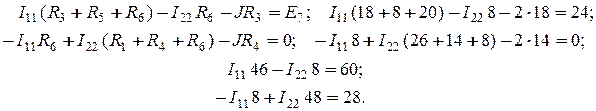
Результат розв’язання системи рівнянь: 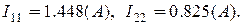
Струми у вітках схеми:
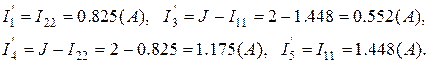
Напругу  , що дорівнює ЕРС еквівалентного генератора
, що дорівнює ЕРС еквівалентного генератора  , для пере-вірки правильності розв’язку знаходимо двома незалежними шляхами.
, для пере-вірки правильності розв’язку знаходимо двома незалежними шляхами.
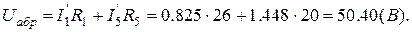
Самостійно перевірте цю напругу іншим шляхом, наприклад:
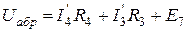
2).Вхідний опір між точками а, б, що дорівнює опору еквівалентного гене-ратора, знаходимо видаленням з активного двополюсника джерел енергії (Рис. П6.1, а).
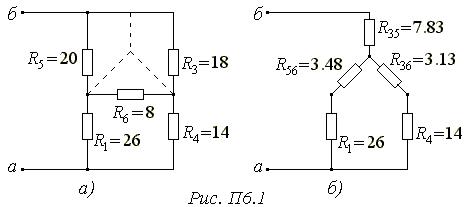
Для спрощення схеми «трикутник»  перетворюється на «зірку»
перетворюється на «зірку» 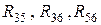 (Рис. П6.1, б).
(Рис. П6.1, б).
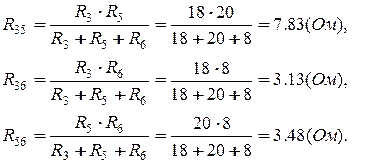
У спрощеній схемі до паралельних віток з послідовно з’єднаними опора-ми  і
і  під’єднаний послідовно опір
під’єднаний послідовно опір  Вхідний еквівалентний опір відносно точок а, б:
Вхідний еквівалентний опір відносно точок а, б:
 .).
.).
3). Струм 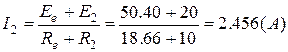 . Це видно із схеми ек-вівалентного генератора (Рис. П6, б)
. Це видно із схеми ек-вівалентного генератора (Рис. П6, б)
Результат такий же, як і при розрахунку іншими методами.
ІІ. Для зміни напряму струму 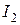 визначаємо нову ЕРС
визначаємо нову ЕРС 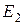 із останньої фор-мули:
із останньої фор-мули:  ;
;
звідки: 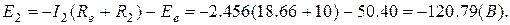
ІІІ. В електричних колах зміна будь-якого одного параметра (ЕРС, опору резистора) викликає зміну напруг та струмів у вітках схеми. В лінійних колах при цьому залежність між напругами і струмами у вітках – лінійна, яка в загальному випадку описується функцією 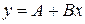 .
.
Для визначення шуканої залежності 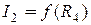 спочатку визначаємо за-лежність між струмами
спочатку визначаємо за-лежність між струмами 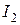 та
та 
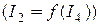 , а потім за методом еквіва-лентного генератора визначаємо залежність між струмом
, а потім за методом еквіва-лентного генератора визначаємо залежність між струмом  та
та 
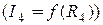 .
.
Із прикладу 3 відомо, що: 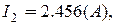
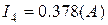 .Залежність між ними виразимо рівнянням:
.Залежність між ними виразимо рівнянням:  Визначаємо коефіцієнти А, В, знаючи струми
Визначаємо коефіцієнти А, В, знаючи струми  для двох значень змінюваного опору
для двох значень змінюваного опору  .
.
1). При 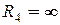 - (розрив) струм
- (розрив) струм 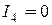 . Струм
. Струм 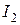 при цьому визначаємо зі схеми кола (Рис. П6.2, а).
при цьому визначаємо зі схеми кола (Рис. П6.2, а).
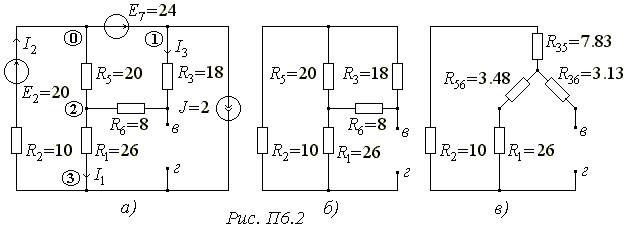
Цю задачу розв’яжемо методом вузлових потенціалів.
Потенціал заземленого вузла  , потенціал першого вузла:
, потенціал першого вузла:
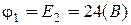 .
.
Визначаються потенціали вузлів 2, 3.
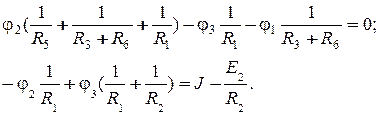
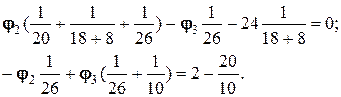
Або: 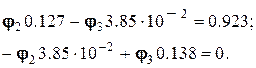
Звідки: j2= 7.941 (В), j3= 2.206 (В).
Струми у вітках:
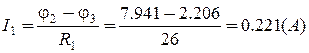 ;
; 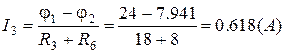 ;
;
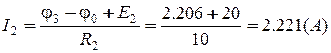 .
.
Отже: 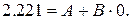 Звідки
Звідки 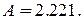
За відомими струмами  , знайденими у прикладі 3 при
, знайденими у прикладі 3 при  визначаємо коефіцієнт В.
визначаємо коефіцієнт В.

 .
.
Залежність струму  від опору
від опору  знаходимо за методом еквівалентного генератора, користуючись відомими струмами у колі на Рис. П6.2, а.
знаходимо за методом еквівалентного генератора, користуючись відомими струмами у колі на Рис. П6.2, а.

Перевірте! Така ж напруга буде при визначенні іншим шляхом:

Опір еквівалентного генератора визначаємо зі схем (Рис.П6.2, б, в).
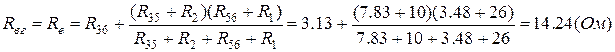 .
.
Тепер маємо:

Дата добавления: 2015-02-13; просмотров: 3193;
