Метод вузлових потенціалів.
Метод базується на першому законі Кірхгофа і законі Ома. Розглянемо коло (Рис. 29).
Кількість незалежних рівнянь , що складаються за першим законом Кірхго-фа на одиницю менше від кількості вуз-лів 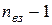 . Один із вузлів кола можна заземлити, розподіл струмів у колі при цьому не зміниться. . Один із вузлів кола можна заземлити, розподіл струмів у колі при цьому не зміниться.
|
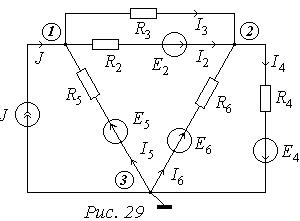
У колі три вузли  . Потенціал вузла 3 вважаємо нульовим:
. Потенціал вузла 3 вважаємо нульовим: 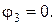 Задаємось напрямками струмів у вітках, як показано на рисунку і записуємо рівняння за першим законом Кірхгофа для для вузлів 1, 2.
Задаємось напрямками струмів у вітках, як показано на рисунку і записуємо рівняння за першим законом Кірхгофа для для вузлів 1, 2.
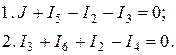

Струми у вітках виражаємо через потенціали відповідних вузлів і параметри віток за законом Ома:
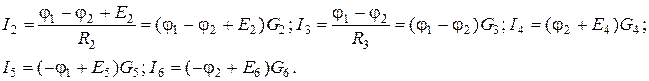
де:  - провідності відповід-них віток.
- провідності відповід-них віток.
Підставляєм вирази для струмів у початкові рівняння:
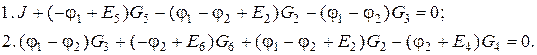
Зводим подібні члени.
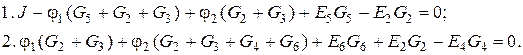
Відомі члени рівнянь переносимо у праву частину:
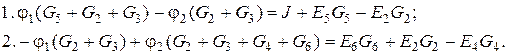
Введем позначення:
 - власна провідність першого вузла (сума провідностей віток, що належать першому вузлу),
- власна провідність першого вузла (сума провідностей віток, що належать першому вузлу),
 - власна провідність другого вузла(сума провідно-стей віток, що належать другому вузлу),
- власна провідність другого вузла(сума провідно-стей віток, що належать другому вузлу),
 - взаємна вузлова провідність між першим і другим вуз-лами.
- взаємна вузлова провідність між першим і другим вуз-лами.
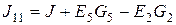 - Вузловий струм першого вузла (алгебраїчна сума джерел струму віток, які належать першому вузлу).
- Вузловий струм першого вузла (алгебраїчна сума джерел струму віток, які належать першому вузлу).
 - вузловий струм другого вузла (алгебраїчна сума джерел струму віток, які належать другому вузлу).
- вузловий струм другого вузла (алгебраїчна сума джерел струму віток, які належать другому вузлу).
При цьому, як бачимо, враховуються струми джерел, еквівалентних дже-релам напруги цих віток.
Увага! Правило знаків.Якщо джерело струму або ЕРС спрямовані до вуз-ла то вони входять у вузловий струм зі знаком «+», інакше – зі знаком «-» . Власні провідності входять у рівняння зі знаком «+», а взаємні –зі знаком «-».
У загальному вигляді рівняння для кола, з двома незалежними вузлами записуються так:
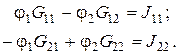
Аналогічно для кола з n незалежними вузлами :

Алгоритм розрахунку електричного кола методом вузлових потенціалів.
1. Приймаємо за нуль потенціал одного із вузлів (заземлюємо його). Цей вузол називається опорним, або залежним.
Увага! Якщо у вітці між двома вузлами є ЕРС без послідовного резистора то, очевидно, потенціали вузлів відрізняються між собою на величину ЕРС. Прийнявши потенціал одного із цих вузлів за нульовий, одержуємо потенціал другого вузла.
2. Складаємо рівняння за методом вузлових потенціалів. Кількість рівнянь дорівнює кількості незалежних вузлів з невідомими потенціалами.
3. Будь-яким способом розв’язуємо систему рівнянь і визначаємо потенціали вузлів.
4. За законом Ома визначаємо струми у вітках схеми.
Розглянемо застосування методу вузлових потенціалів для задачі , яку було розраховано методом контурних струмів.
Приклад 2. Розрахувати методом вузлових потенціалів усі струми у колі Рис. П2. У колі п’ять вузлів. За методом вузлових потенціалів потрібно скласти чотири рівняння, але у колі є вітка з ЕРС (E7), послідовно з якою не увімкнено резистор. Прийнявши за нуль потенціал вузла  одержимо
одержимо 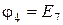 =24 (В). Тому кількість рівнянь зменшується до трьох:
=24 (В). Тому кількість рівнянь зменшується до трьох:
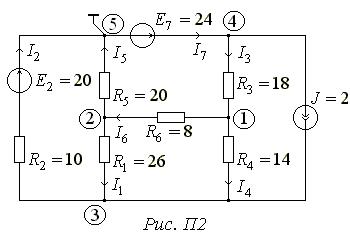
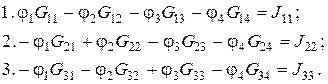
Виражаючи власні і взаємні провідності і вузлові струми через задані пара-метри кола, одержимо:


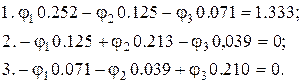
Розв’язавши систему рівнянь, одержимо потенціали вузлів:
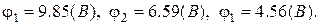
За законом Ома знаходимо струми у вітках кола.

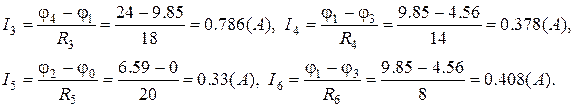
Струм 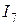 знаходиться за першим законом Кірхгофа
знаходиться за першим законом Кірхгофа
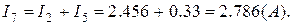
Знайдені струми такі ж, як і при розрахунку методом контурних струмів.
Дата добавления: 2015-02-13; просмотров: 3519;
