Расчет и моделирование параметров усилителя на постоянном токе
КРАТКАЯ ТЕОРИЯ.Деформацией твердого тела называют изменение его размеров и формы. Деформация обычно сопровождается изменением объема тела.
Деформации вызываются действием на него внешних сил или изменением температуры. При деформации происходят смещения частиц, находящихся в узлах кристаллических решеток твердых тел, из первоначальных положений равновесия в новые. Этому смещению препятствуют силы взаимодействия между частицами. В результате в деформируемом теле возникают внутренние упругие силы.
Виды деформации:
1) растяжение (сжатие);
2) кручение;
3) изгиб;
4) сдвиг и т.д.
Деформации, при которых деформируемое тело после снятия нагрузки возвращается в первоначальное состояние,называютсяупругими.Деформации, при которых деформируемое тело после снятия нагрузки не возвращается в первоначальное состояние, называются неупругими. В этом случае деформация тела сопровождается необратимой перестройкой его кристаллической решетки.
Упругие деформации имеют место тогда, когда внешние силы, вызывающие деформацию, не превосходят некоторого определенного для каждого конкретного тела предела, называемого пределом упругости.
При установившейся упругой деформации результирующая внутренних упругих сил, возникающих в теле, в любом сечении тела уравновешивает внешние силы, действующие на тело.
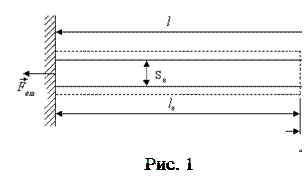 Пусть стержень длиной
Пусть стержень длиной 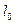 и площадью поперечного сечения
и площадью поперечного сечения 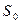 растянут внешними силами
растянут внешними силами 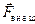 (рис. 1).
(рис. 1).
После установления деформации стержень принимает длину 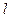 и площадь поперечного сечения
и площадь поперечного сечения  (причем
(причем 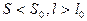 ). Эту деформацию характеризуют величинами:
). Эту деформацию характеризуют величинами:
1. Абсолютная деформация – физическая величина, равная разности конечного и начального размеров деформируемого стержня
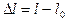 ,
,
где 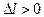 при деформации растяжения,
при деформации растяжения,  деформации сжатия.
деформации сжатия.
2. Относительная деформация – физическая величина, равная отношению абсолютной деформации к первоначальному размеру тела:
 .
.
3. Механическое напряжение – физическая величина, показывающая силу, приходящуюся на единицу площади поперечного сечения деформируемого тела:
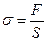 .
.
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности – тангенциальным.
Английский физик Р. Гук в 1675 г. опытным путем установил, что напряжение, возникающее в упруго деформированном теле, прямо пропорцианально величине относительной деформации:
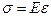 ,
,
где  - постоянная, зависящая от свойств вещества, которая носит название модуля Юнга.
- постоянная, зависящая от свойств вещества, которая носит название модуля Юнга.
Из закона Гука следует выражение для растягивающей (сжимающей) силы:
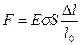 .
.
где 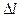 – абсолютное удлинение, вызванное силой F, l0 – первоначальная длина тела.
– абсолютное удлинение, вызванное силой F, l0 – первоначальная длина тела.
При рассмотрении неоднородных деформаций в теории упругости выделяются “малые”, макроскопические объемы, для которых деформацию считают однородной (например, при деформациях кручения, изгиба). Каждый мысленно выделенный объем деформированной среды взаимодействует с окружающим его объемом через свою поверхность раздела, и силы пропорциональны площади этой поверхности.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
В качестве объекта исследования выбрана полимерная пленка с поперечным сечением 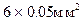 . Длина пленки
. Длина пленки 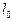 измеряется перед опытом. Схема установки представлена на рис. 2.
измеряется перед опытом. Схема установки представлена на рис. 2.
|
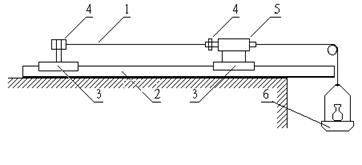
1 – пленка; 2 – станина установки; 3 – закрепленные рейтеры; 4 – узлы крепления пленки; 5 – измеритель удлинения пленки (микрометрический индикатор перемещения с ценой деления 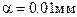 ); 6 – набор грузов с заданными массами.
); 6 – набор грузов с заданными массами.
 Цель работы: изучение зависимости относительного удлинения e от механического напряжения s, порожденного силой растяжения
Цель работы: изучение зависимости относительного удлинения e от механического напряжения s, порожденного силой растяжения 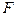 . Эту зависимость принято определять соотношением
. Эту зависимость принято определять соотношением 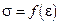 . Для достаточно пластичных материалов графики функций
. Для достаточно пластичных материалов графики функций 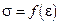 приведены на рис. 4. Кривые 0–а–1 соответствуют деформации растяжения при увеличении силы растяжения; 1–б–2 – уменьшение силы растяжения. В области малых деформаций (
приведены на рис. 4. Кривые 0–а–1 соответствуют деформации растяжения при увеличении силы растяжения; 1–б–2 – уменьшение силы растяжения. В области малых деформаций ( 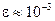 ) кривые увеличения нагрузки имеют прямолинейный участок; здесь деформация будет упругой и справедлив закон Гука. В области больших деформаций появляется отклонение от линейной зависимости, и говорят о неупругой (пластичной) деформации.
) кривые увеличения нагрузки имеют прямолинейный участок; здесь деформация будет упругой и справедлив закон Гука. В области больших деформаций появляется отклонение от линейной зависимости, и говорят о неупругой (пластичной) деформации.
В целом кривая может быть описана многочленом с различными степенями e в виде:
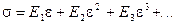 ,
,
где 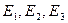
 - постоянные величины.
- постоянные величины.
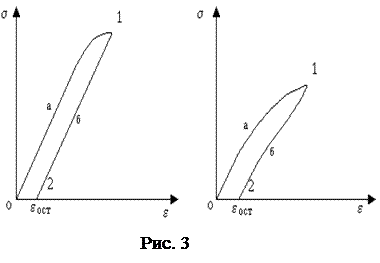
Если при увеличении силы растяжения проявляется неупругая деформация, то кривые “нагрузки” и “разгрузки” не совпадают и при полном снятии нагрузки e оказывается не равной нулю. Говорят об “остаточной” деформации. Несовпадение кривых “нагрузки” и “разгрузки” носит название упругого гистерезиса. Типичные кривые для металлов (а) и полимеров (резиноподобных материалов) (б) имеют вид рис. 3.
При деформации иногда существенно проявляется конечность времени установления деформации при постоянной приложенной силе растяжения. Величина времени для различных материалов колеблется в достаточно широких пределах (от 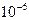 с до
с до  с и более).
с и более).
Это явление обусловлено достаточно разнообразными причинами (типичными являются: упругое последействие и ползучесть материала).
ПРОВЕДЕНИЕ ЭКПЕРИМЕНТА
Перед проведением эксперимента определяется: длина пленки 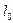 , начальное показание индикатора удлинения
, начальное показание индикатора удлинения 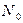 , рассчитывается площадь поперечного сечения пленки
, рассчитывается площадь поперечного сечения пленки 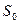 по размерам сечения
по размерам сечения 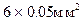 .
.
Установка нагружается грузами, помещаемыми на чашку 6 (рис. 3). Постепенно сила растяжения доводится до 10–15 Н, затем разгружается до конца последовательным снятием перегрузков с чаши.
Так как деформация устанавливается не сразу, отсчет величины удлинения по индикатору производится не ранее, чем через минуту после установки (снятия) каждого перегрузка на чашку. Кроме этого, необходимо использовать “легкое” постукивание по нити, перекинутой через блок, для ликвидации торможения штоков индикатора за счет сил трения. При этом показания индикатора N будут меняться, три из них следует отсчитать и занести в таблицу эксперимента для каждой силы.
Таблицу эксперимента удобно выбрать в виде:
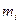 , г , г
| 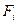 , Н , Н
| 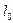 , мм , мм
| 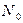
| 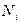
| 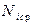
| 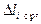 мм
мм
| 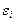
| 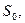 мм2 мм2
| 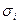 , ,
|
| …… | ..... | .... | |||||||
В “нулевой” строке записываются: 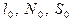 . В каждой последующей строке записываются деления индикатора (с учетом двух шкал)
. В каждой последующей строке записываются деления индикатора (с учетом двух шкал) 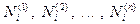 .
.
Далее рассчитываются:
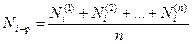 ,
, 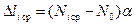 , где a=0.01мм,
, где a=0.01мм, 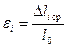 и
и 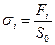 .
.
Результаты расчета заносятся в таблицу. По полученным данным  и
и 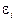 строятся графики
строятся графики 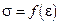 для “прямого” и “обратного” хода нагрузки.
для “прямого” и “обратного” хода нагрузки.
ОБРАБОТКА РЕЗУЛЬТАТОВ. Так как экспериментально найденная зависимость 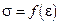 нелинейная, то можно предположить, что она соответствует уравнению:
нелинейная, то можно предположить, что она соответствует уравнению: 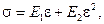 где
где 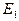 равно модулю упругости Юнга
равно модулю упругости Юнга 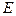 ,
, 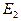 характеризует неупругую деформацию (
характеризует неупругую деформацию ( 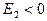 ). Для нахождения
). Для нахождения 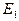 и
и 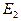 по экспериментальным данным удобно использовать статистический метод обработки результатов опытов, называемый методом наименьших квадратов. Согласно этому методу
по экспериментальным данным удобно использовать статистический метод обработки результатов опытов, называемый методом наименьших квадратов. Согласно этому методу 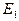 и
и 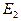 определяются соотношениями:
определяются соотношениями:
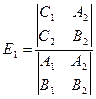 ,
, 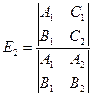 ,
,
включающими детерминанты из чисел: 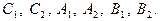 Эти числа выражаются через
Эти числа выражаются через  и
и 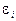 (для кривой “нагрузки”) в виде:
(для кривой “нагрузки”) в виде: 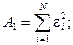
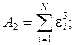
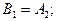
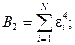
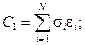
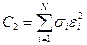 .
.
Определив 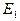 и
и 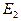 , следует рассчитать теоретическую кривую
, следует рассчитать теоретическую кривую 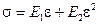 и сравнить с экспериментальными данными, начертив ее на графике эксперимента.
и сравнить с экспериментальными данными, начертив ее на графике эксперимента.
Таблица 1.1
| H11э | 
| h11б | 
|
| H12э | 
| h12б | 
|
| H21э | 
| h21б | 
|
| H22э | 
| h22б | 
|
На рис. 1.6 показан процесс определения h-параметров по входной ВАХ транзистора, а на рис. 1.7 - по выходной. Из рисунков видно, что значения h-параметров не являются постоянными для конкретного транзистора и зависят от режима по постоянному току (рабочей точки покоя транзистора) - значений постоянных составляющих токов и напряжений на входе и выходе транзистора. Поэтому в справочной литературе при указании h-параметров обязательно указывается и режим, при котором произведены измерения.
Значения h-параметров также зависят от частоты переменного сигнала и температуры окружающей среды.

 ;
;
 .
.
Рис. 1.6 - Определение h-параметров по входной ВАХ транзистора

 ,
,

Рис. 1.7 - Определение h-параметров по выходной ВАХ транзистора
1.5 Расчет усилителей на постоянном токе
 Электронный усилитель – устройство, предназначенное для усиления напряжения, тока и/или мощности электрических сигналов. Схематично структуру усилителя можно представить (Рис. 1.8) состоящей из: маломощного источника входного сигнала Р1, источника мощности Р0, усилительного элемента У и нагрузки Р2.
Электронный усилитель – устройство, предназначенное для усиления напряжения, тока и/или мощности электрических сигналов. Схематично структуру усилителя можно представить (Рис. 1.8) состоящей из: маломощного источника входного сигнала Р1, источника мощности Р0, усилительного элемента У и нагрузки Р2.
Усилитель реализует под управлением источника входного сигнала передачу энергии от источника мощности к нагрузке. Ключевым элементом, регулирующим эту передачу, является транзистор: биполярный или полевой.



 |
Использование в усилителе биполярного транзистора предполагает включение его по одной из трех возможных схем: с общим эмиттером (ОЭ), с общей базой (ОБ) или общим коллектором (ОК). На рис. 1.9 показана схема наиболее распространенного усилителя на базе биполярного транзистора – с ОЭ, т.е. эмиттер является общим электродом для входной и выходной цепей. Входное напряжение uвх от источника усиливаемого сигнала ес подается на усилительный каскад через разделительный конденсатор С1.
Работу усилителя с ОЭ можно проиллюстрировать с помощью вольт-амперных характеристик (ВАХ) транзистора (Рис. 1.10): входной характеристики Iб = f(Uбэ) и семейства выходных Iк = f(Uкэ) при разных токах базы.
Для коллекторной цепи усилителя на постоянном токе (Рис. 1.9) можно записать: Uкэ =Ек - RкIк. Графическим решением этого уравнения является прямая, представленная на семействе выходных ВАХ и называемая линией нагрузки по постоянному току. Её можно построить по двум точкам: соответствующей режиму холостого хода (координаты точки Iк=0 и Uк=Ек) и короткого замыкания (координаты точки Iк=Ек/Rк и Uк=0). Точки пересечения линии нагрузки с выходными характеристиками транзистора определяют ток Iк и напряжение на транзисторе Uкэ при любом заданном значении тока базы Iб. Конкретное значение данных параметров (координат) задает текущее положение рабочей точки как на выходе, так и на входе усилителя.
Анализ уравнения, описывающего линию нагрузки, показывает, что наклон данной линии определяется величиной Rк. В реальных усилителях это значение колеблется в пределах от нескольких Омов до нескольких килоОмов.
В усилителе действуют, по крайней мере, два электрических источника: источник постоянной э.д.с. Ек и источник усиливаемого переменного напряжения ес. Первый из них обеспечивает требуемый режим покоя (режим работы по постоянному току), который на рис. 1.10 определяется точкой О (рабочая точка в режиме покоя), т.е. создает постоянные составляющие тока и напряжения на входе и выходе усилителя: I0б и U0бэ, I0к и U0кэ. Для усиления входных сигналов с минимальными линейными искажениями начальное положение рабочей точки целесообразно выбирать на середине линии нагрузки, т.е. с координатами
U0кэ » Ек/2; I0к » (Ек/2)/Rк. (1.8)
При этом
I0б » I0к/h21э, (1.9)
а U0бэ » 0.3 В для германиевых и U0бэ » 0.7 В для кремниевых транзисторов.
Конденсатор С1 включен на входе усилителя для того, чтобы:
· не пропускать постоянную составляющую усиливаемого сигнала на вход усилителя;
· не создавать постоянной составляющей тока в источнике усиливаемого сигнала ес за счет действия источника питания Ек.
Разделительный конденсатор С2, в свою очередь, задерживает постоянную составляющую коллекторного напряжения и пропускает в нагрузку усилителя только переменную составляющую напряжения uк, являющуюся выходным напряжением усилителя.
Задание постоянных составляющих токов и напряжений на входе и выходе усилителя реализуется двумя основными способами:
· фиксированным напряжением база-эмиттер (Рис. 1.11);
· фиксированным током базы (Рис. 1.12).
На рис. 1.11 приведен пример использования первого способа. Схема включает на входе резисторный делитель, при этом
UR2= U0бэ=IдR2. (1.10)
Оба последних параметра заранее не фиксированы, т.е. могут выбираться произвольно. Обычно задаются значением Iд, соблюдая соотношение
Iд/I0б ³ 10. (1.11)
Тогда R2 = U0бэ/Iд. Учитывая, что UR1= Ек - U0бэ= (Iд + I0б)R1, находится требуемое значение сопротивления R1 = (Ек - U0бэ)/(Iд + I0б).
Для схемы на рис. 1.12 можно записать URб=Ек-U0бэ=I0бRб.
Тогда Rб =(Ек - U0бэ)/I0б. Так как обычно Ек >> U0бэ, то в инженерных расчетах можно использовать приближенную формулу вида Rб » Ек/I0б.
При изменении температуры окружающей среды входная ВАХ транзистора смещается по горизонтали, а выходная – по вертикали, что приводит к смещению начального положения рабочих точек как на входе, так и на выходе усилителя. При большой амплитуде выходного сигнала указанное явление может привести к заходу рабочей точки при движении по линии нагрузки в область насыщения или отсечки, что обуславливает искажение формы выходного сигнала в виде зарезания вершин выходной синусоиды.

Для борьбы с данным явлением используются два основных метода:
1) термокомпенсация – на основе нелинейных элементов, параметры которых определенным образом зависят от температуры;
2) термостабилизация, базирующаяся на механизме отрицательной обратной связи (ООС).
На практике обычно используется второй метод, предполагающий включение в состав усилителя резистора Rэ (Рис. 1.13) для создания ООС. Ёе механизм иллюстрируется следующей логической цепочкой: предположим, что температура окружающей среды выросла, тогда:
Т ® I0к ® I0э (так как I0к = aI0э + I0кэ) ® URэ = I0эRэ ® ¯U0бэ = UR2 – URэ ® ¯I0б ® ¯D I0к.
При этом предполагается, что напряжение UR2 остается практически постоянным, так как Iд >> I0б.

ООС не позволяет полностью устранить влияние температуры на начальное положение рабочей точки, но уменьшает его. Количественная оценка такого уменьшения производится с помощью коэффициента нестабильности коллекторного тока S:
S = DI0к/DIк,
где DIк – приращение тока Iк в схеме с идеальной термостабилизацией (с минимальным изменением тока Iк).
Значение S для конкретной схемы рассчитывается по формуле
 , (1.12)
, (1.12)
где Rб=R1∥R2.
Анализ выражения (1.12) показывает, что:
(Rб ® 0) Þ (S ® 1); (Rэ ® 0) Þ (S ® b);
(Rб ® ¥) Þ (S ® b); (Rэ ® ¥) Þ (S ® 1),
т.е. уменьшение Rб ведет к улучшению термостабилизации, а увеличение – к ухудшению. Обратный эффект оказывает на термостабилизацию величина резистора Rэ. Однако увеличение данного сопротивления ведет к увеличению номинала Ек при заданных Rк и U0кэ. Поэтому величина резистора Rэ обычно ограничивается значением 200¸300 Ом. Введение в схему Rэ предполагает, что наклон линии нагрузки (Рис. 1.10) уже определяется суммарным значением Rк+Rэ (при инженерных расчетах предполагается, что I0к » I0э), а UR2=U0бэ+URэ.
2. Практическое выполнение задания
2.1 Построение статических характеристик транзистора
1) cмоделировать схему, представленную рис. 2.1 (тип биполярного транзистора задается в соответствии с номером варианта (таблица 2.1));
 |
Рис. 2.1
Таблица 2.1
| № варианта | Марка транзистора | ЕК, В | RК, Ом | RЭ, Ом |
| ВС107 | ||||
| ВС107А | ||||
| ВD239 | ||||
| 2N2218 | ||||
| 2N2222 | ||||
| 2N2222А | ||||
| 2N3904 | ||||
| 2N4401 |
2) снять показания измерительных приборов для построения семейства входных ВАХ исследуемого транзистора. Результаты измерений записать в табл. 2.2;
3) по полученным данным на миллиметровой бумаге построить семейство входных ВАХ транзистора  .
.
4) снять показания измерительных приборов для построения семейства выходных ВАХ исследуемого транзистора. Результаты измерений записать в табл. 2.3;
Таблица 2.2
| Uкэ,В | ||||||||||
 ,mA ,mA
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
 , В , В
|
Таблица 2.3
 , мкА , мкА
| |||||||||
 , В , В
| |||||||||
 ,mA ,mA
| |||||||||
 ,mA ,mA
| |||||||||
 ,mA ,mA
| |||||||||
 ,mA ,mA
| |||||||||
 ,mA ,mA
| |||||||||
5) по полученным данным на миллиметровой бумаге построить семейство выходных ВАХ транзистора  ;
;
6) на семействе выходных ВАХ транзистора построить линию нагрузки по постоянному току, использую данные табл. 2.1 (ЕК и RK);
7) задать начальное положение рабочей точки O (что соответствует примерно середине усилительного участка нагрузочной прямой);
8) рассчитать h - параметры транзистора относительно установленной рабочей точки;
9) используя формулы, представленные в таблице 1.1, рассчитать h-параметры для того же транзистора, включенного по схеме с общей базой.
2.2 Измерение коэффициента усиления по току в статическом режиме
1) смоделировать схему, представленную на рис. 2.2;
|
|
|

Рис.2.2
В цепь эмиттера включен источник тока, задающий ток в статическом режиме. Амперметрами измеряются постоянные токи в цепях базы и коллектора Iб и Iк . Коэффициент усиления по току в схеме с общим эмиттером в статическом режиме (интегральная характеристика) рассчитывается по формуле: h21Э= Iк /Iб.
2) снять показания измерительных приборов и результаты измерений записать в табл. 2.4;
Таблица 2.4
| Iэ,мА | 0,1 | ||||||||
| Iб,мА | |||||||||
| Iк,мА | |||||||||
| h21Э |
3) по полученным значениям построить зависимость В=f(Iк), из которой определить максимальное значение h21Э для статического режима работы транзистора.
2.3 Измерение емкости коллекторно-базового перехода Ск
1) смоделировать схему, представленную на рис.2.3;
|

Рис. 2.3
Емкость обратносмещенного коллекторно-базового перехода Ск образует с сопротивлением резистора Rк делитель напряжения.
3) измерить значения постоянного U1 и переменного U2 напряжений;
4) рассчитать емкость Ск по формуле:
 ,
,
где F – частота источника синусоидального напряжения.
Измерения производятся при различных значениях постоянного напряжения коллектор-база путем изменения напряжения питания от 0,1 до 10 В.
5) результаты измерений и расчетов занести в табл. 2.5.
6) построить зависимость Ск=f(Uкб).
Таблица 2.5
| Uкб,В | 0.1 | |||||||||
| U1,мВ | ||||||||||
| U2,мВ | ||||||||||
| Ск,пкФ |
Расчет и моделирование параметров усилителя на постоянном токе
Для моделирования усилительного каскада, представленного на рис. 1.13, выполнить в предложенной ниже последовательности расчет его параметров.
1) рассчитать предварительное значение тока базы покоя I0Б (см. ф. 1.9);
2) используя соотношение 1.11, задаться значением тока делителя IД;
3) найти значение резистора R2;
4) определить значение резистора R1;
5) рассчитать коэффициент нестабильности коллекторного тока S (см. ф. 1.12).
6) смоделировать схему усилителя на биполярном транзисторе с ОЭ с эмиттерной термостабилизацией (см. рис. 1.13), установив полученные значения сопротивлений резисторов в цепях базового делителя напряжения. Измерить все постоянные токи, протекающие в цепях транзистора и падения напряжений на всех участках цепи. Сравнить полученные значения с расчетными.
По окончании выполнения работы и оформления отчета каждый студент должен ответить письменно на два контрольных вопроса. Номера вопросов для каждого варианта представлены в таблице 2.6.
Таблица 2.6
| № варианта | № вопроса | № варианта | № вопроса |
| 1, 10 | 18, 21 | ||
| 2, 15 | 22, 15 | ||
| 3, 17 | 23, 14 | ||
| 4, 19 | 24, 3 | ||
| 5, 20 | 25, 4 | ||
| 6, 21 | 26, 5 | ||
| 7, 27 | 29, 1 | ||
| 8, 28 | 2, 19 | ||
| 9, 30 | 4, 28 | ||
| 11, 23 | 7, 17 | ||
| 12, 24 | 9, 30 | ||
| 13, 25 | 3, 27 | ||
| 14, 26 | 5, 15 | ||
| 16, 6 | 16, 10 |
| <== предыдущая лекция | | | следующая лекция ==> |
| ИССЛЕДОВАНИЕ ДЕФОРМАЦИИ РАСТЯЖЕНИЯ ТВЕРДОГО ТЕЛА | | | СРАВНЕНИЕ ЛОБОВЫХ СОПРОТИВЛЕНИЙ ТЕЛ РАЗЛИЧНОЙ ФОРМЫ |
Дата добавления: 2015-02-13; просмотров: 1454;
