ИССЛЕДОВАНИЕ ДЕФОРМАЦИИ РАСТЯЖЕНИЯ ТВЕРДОГО ТЕЛА
1. Как графически можно представить гармоническое колебание?
2. Биения. Что такое биения? Какова частота биений?
3. Получить уравнение траектории материальной точки, участвующей одновременно в двух взаимно-перпендикулярных колебаниях с одинаковой частотой.
4. Определить траекторию движения материальной точки в зависимости от соотношения фаз складываемых колебаний.
5. Дайте определение фигуры Лиссажу, от каких параметров зависит вид фигур Лиссажу.
6. Какую информацию можно получить, анализируя вид фигуры Лиссажу?
7. По указанию преподавателя графическим методом сложить два взаимно перпендикулярных колебания (данные в таблице 1).
8. Получить результирующую амплитуду сложения колебаний одинакового направления и частоты.
ИССЛЕДОВАНИЕ ДЕФОРМАЦИИ РАСТЯЖЕНИЯ ТВЕРДОГО ТЕЛА
КРАТКАЯ ТЕОРИЯ.Деформацией твердого тела называют изменение его размеров и формы. Деформация обычно сопровождается изменением объема тела.
Деформации вызываются действием на него внешних сил или изменением температуры. При деформации происходят смещения частиц, находящихся в узлах кристаллических решеток твердых тел, из первоначальных положений равновесия в новые. Этому смещению препятствуют силы взаимодействия между частицами. В результате в деформируемом теле возникают внутренние упругие силы.
Виды деформации:
1) растяжение (сжатие);
2) кручение;
3) изгиб;
4) сдвиг и т.д.
Деформации, при которых деформируемое тело после снятия нагрузки возвращается в первоначальное состояние,называютсяупругими.Деформации, при которых деформируемое тело после снятия нагрузки не возвращается в первоначальное состояние, называются неупругими. В этом случае деформация тела сопровождается необратимой перестройкой его кристаллической решетки.
Упругие деформации имеют место тогда, когда внешние силы, вызывающие деформацию, не превосходят некоторого определенного для каждого конкретного тела предела, называемого пределом упругости.
При установившейся упругой деформации результирующая внутренних упругих сил, возникающих в теле, в любом сечении тела уравновешивает внешние силы, действующие на тело.
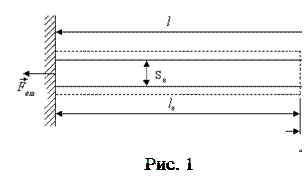 Пусть стержень длиной
Пусть стержень длиной 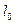 и площадью поперечного сечения
и площадью поперечного сечения 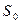 растянут внешними силами
растянут внешними силами 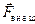 (рис. 1).
(рис. 1).
После установления деформации стержень принимает длину 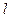 и площадь поперечного сечения
и площадь поперечного сечения  (причем
(причем 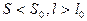 ). Эту деформацию характеризуют величинами:
). Эту деформацию характеризуют величинами:
1. Абсолютная деформация – физическая величина, равная разности конечного и начального размеров деформируемого стержня
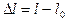 ,
,
где 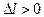 при деформации растяжения,
при деформации растяжения,  деформации сжатия.
деформации сжатия.
2. Относительная деформация – физическая величина, равная отношению абсолютной деформации к первоначальному размеру тела:
 .
.
3. Механическое напряжение – физическая величина, показывающая силу, приходящуюся на единицу площади поперечного сечения деформируемого тела:
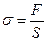 .
.
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности – тангенциальным.
Английский физик Р. Гук в 1675 г. опытным путем установил, что напряжение, возникающее в упруго деформированном теле, прямо пропорцианально величине относительной деформации:
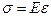 ,
,
где  - постоянная, зависящая от свойств вещества, которая носит название модуля Юнга.
- постоянная, зависящая от свойств вещества, которая носит название модуля Юнга.
Из закона Гука следует выражение для растягивающей (сжимающей) силы:
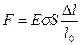 .
.
где 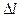 – абсолютное удлинение, вызванное силой F, l0 – первоначальная длина тела.
– абсолютное удлинение, вызванное силой F, l0 – первоначальная длина тела.
При рассмотрении неоднородных деформаций в теории упругости выделяются “малые”, макроскопические объемы, для которых деформацию считают однородной (например, при деформациях кручения, изгиба). Каждый мысленно выделенный объем деформированной среды взаимодействует с окружающим его объемом через свою поверхность раздела, и силы пропорциональны площади этой поверхности.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
В качестве объекта исследования выбрана полимерная пленка с поперечным сечением 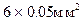 . Длина пленки
. Длина пленки 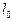 измеряется перед опытом. Схема установки представлена на рис. 2.
измеряется перед опытом. Схема установки представлена на рис. 2.
|
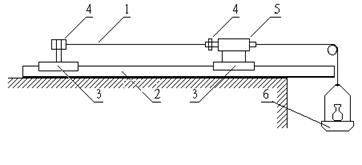
1 – пленка; 2 – станина установки; 3 – закрепленные рейтеры; 4 – узлы крепления пленки; 5 – измеритель удлинения пленки (микрометрический индикатор перемещения с ценой деления 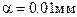 ); 6 – набор грузов с заданными массами.
); 6 – набор грузов с заданными массами.
 Цель работы: изучение зависимости относительного удлинения e от механического напряжения s, порожденного силой растяжения
Цель работы: изучение зависимости относительного удлинения e от механического напряжения s, порожденного силой растяжения  . Эту зависимость принято определять соотношением
. Эту зависимость принято определять соотношением  . Для достаточно пластичных материалов графики функций
. Для достаточно пластичных материалов графики функций  приведены на рис. 4. Кривые 0–а–1 соответствуют деформации растяжения при увеличении силы растяжения; 1–б–2 – уменьшение силы растяжения. В области малых деформаций (
приведены на рис. 4. Кривые 0–а–1 соответствуют деформации растяжения при увеличении силы растяжения; 1–б–2 – уменьшение силы растяжения. В области малых деформаций ( 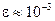 ) кривые увеличения нагрузки имеют прямолинейный участок; здесь деформация будет упругой и справедлив закон Гука. В области больших деформаций появляется отклонение от линейной зависимости, и говорят о неупругой (пластичной) деформации.
) кривые увеличения нагрузки имеют прямолинейный участок; здесь деформация будет упругой и справедлив закон Гука. В области больших деформаций появляется отклонение от линейной зависимости, и говорят о неупругой (пластичной) деформации.
В целом кривая может быть описана многочленом с различными степенями e в виде:
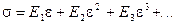 ,
,
где 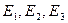
 - постоянные величины.
- постоянные величины.
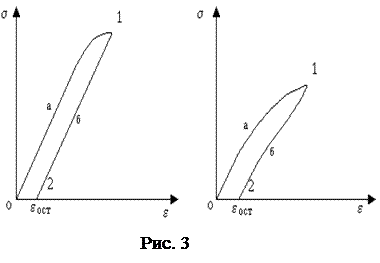
Если при увеличении силы растяжения проявляется неупругая деформация, то кривые “нагрузки” и “разгрузки” не совпадают и при полном снятии нагрузки e оказывается не равной нулю. Говорят об “остаточной” деформации. Несовпадение кривых “нагрузки” и “разгрузки” носит название упругого гистерезиса. Типичные кривые для металлов (а) и полимеров (резиноподобных материалов) (б) имеют вид рис. 3.
При деформации иногда существенно проявляется конечность времени установления деформации при постоянной приложенной силе растяжения. Величина времени для различных материалов колеблется в достаточно широких пределах (от 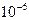 с до
с до  с и более).
с и более).
Это явление обусловлено достаточно разнообразными причинами (типичными являются: упругое последействие и ползучесть материала).
ПРОВЕДЕНИЕ ЭКПЕРИМЕНТА
Перед проведением эксперимента определяется: длина пленки 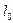 , начальное показание индикатора удлинения
, начальное показание индикатора удлинения 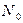 , рассчитывается площадь поперечного сечения пленки
, рассчитывается площадь поперечного сечения пленки 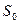 по размерам сечения
по размерам сечения 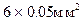 .
.
Установка нагружается грузами, помещаемыми на чашку 6 (рис. 3). Постепенно сила растяжения доводится до 10–15 Н, затем разгружается до конца последовательным снятием перегрузков с чаши.
Так как деформация устанавливается не сразу, отсчет величины удлинения по индикатору производится не ранее, чем через минуту после установки (снятия) каждого перегрузка на чашку. Кроме этого, необходимо использовать “легкое” постукивание по нити, перекинутой через блок, для ликвидации торможения штоков индикатора за счет сил трения. При этом показания индикатора N будут меняться, три из них следует отсчитать и занести в таблицу эксперимента для каждой силы.
Таблицу эксперимента удобно выбрать в виде:
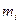 , г , г
| 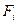 , Н , Н
| 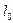 , мм , мм
| 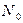
| 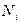
| 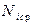
| 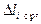 мм
мм
| 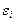
| 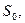 мм2 мм2
| 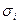 , ,
|
| …… | ..... | .... | |||||||
В “нулевой” строке записываются: 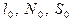 . В каждой последующей строке записываются деления индикатора (с учетом двух шкал)
. В каждой последующей строке записываются деления индикатора (с учетом двух шкал) 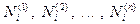 .
.
Далее рассчитываются:
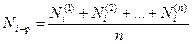 ,
, 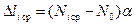 , где a=0.01мм,
, где a=0.01мм, 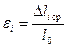 и
и 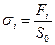 .
.
Результаты расчета заносятся в таблицу. По полученным данным  и
и 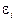 строятся графики
строятся графики 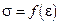 для “прямого” и “обратного” хода нагрузки.
для “прямого” и “обратного” хода нагрузки.
ОБРАБОТКА РЕЗУЛЬТАТОВ. Так как экспериментально найденная зависимость 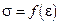 нелинейная, то можно предположить, что она соответствует уравнению:
нелинейная, то можно предположить, что она соответствует уравнению: 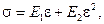 где
где 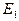 равно модулю упругости Юнга
равно модулю упругости Юнга 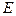 ,
, 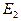 характеризует неупругую деформацию (
характеризует неупругую деформацию ( 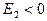 ). Для нахождения
). Для нахождения 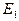 и
и 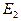 по экспериментальным данным удобно использовать статистический метод обработки результатов опытов, называемый методом наименьших квадратов. Согласно этому методу
по экспериментальным данным удобно использовать статистический метод обработки результатов опытов, называемый методом наименьших квадратов. Согласно этому методу 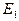 и
и 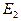 определяются соотношениями:
определяются соотношениями:
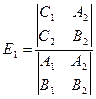 ,
, 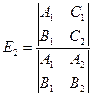 ,
,
включающими детерминанты из чисел: 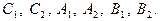 Эти числа выражаются через
Эти числа выражаются через  и
и 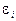 (для кривой “нагрузки”) в виде:
(для кривой “нагрузки”) в виде: 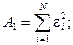
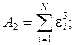
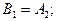
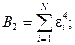
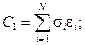
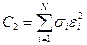 .
.
Определив 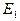 и
и 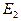 , следует рассчитать теоретическую кривую
, следует рассчитать теоретическую кривую 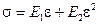 и сравнить с экспериментальными данными, начертив ее на графике эксперимента.
и сравнить с экспериментальными данными, начертив ее на графике эксперимента.
| <== предыдущая лекция | | | следующая лекция ==> |
| Это колебания с амплитудой, изменяюшейся по закону | | | Расчет и моделирование параметров усилителя на постоянном токе |
Дата добавления: 2015-02-13; просмотров: 2045;
