Неповністю сформульовані моделі операцій. Об'єднання операцій.

Можна розрізняти два види цілей і відповідних критеріїв ефективності:

I. «Якісні» цілі, які можуть бути тільки досягнені або не досягнені. Всі дії, що приводять до досягнення мети, однаково придатні; так само всі дії, що не приводять до досягнення мети, однаково непридатні.

При цьому критерій ефективності повинен набувати тільки два значення, наприклад, 1 (у випадку успіху) і 0 (у протилежному випадку) або 1 і (якщо потрібно підкреслити повну неприйнятність недосягнення мети).

При «якісній» меті визначення мети передує означенню критерію ефективності.

Простота такого критерію оманлива, оскільки функціональна залежність величини критерію від стратегій і неконтрольованих факторів може бути вельми складною.

II. Кількісне означення мети полягає у прагненні збільшити (або зменшити) значення деякої величини, залежність якої від біжучих характеристик процесу (фазових координат) й утворює критерій ефективності операції. Таким чином, тут формулювання критерію ніби передує означенню мети операції.

В дійсності часто спочатку мета операції формулюється якісно. Проте наявність, наприклад, випадкових факторів робить випадковим і результат операції, тому здійснюється перехід до іншої «більш досяжної» мети операції, яка вже виявляється метою другого типу, утвореною на базі попередньої.

Іноді з'являються оманливі формулювання першого типу, у яких відсутній зв'язок між фазовими координатами і результатом операції. Наприклад, мета – виграш війни – в дійсності не є метою операції, а гаслом, непридатним для дослідження операцій. Відсутність еквівалентної математичної заміни гасла приводить до стану невизначеності або до запровадження критерію другого типу, який не має категоричного характеру. Така ситуація – не провина дослідника, а наслідок нечіткого розуміння своїх цілей оперуючою стороною.

На жаль, у більшості задач, що мають практичне значення, вибір показника ефективності не простий і розв'язується неоднозначно. Наслідком невизначених ситуацій часто є неповністю сформульовані моделі операцій, в яких немає єдиного критерію ефективності у тому розумінні, що вказувалось раніше. Досліджувана операція розпадається на дрібніші операції, кожна з яких має свою мету і, отже, свій критерій ефективності 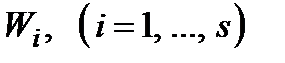. Таким чином, замість одного критерію ефективності з'являється вектор-функція 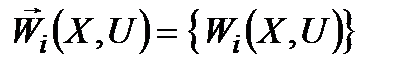( 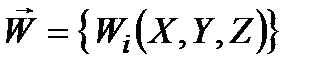) контрольованих і неконтрольованих факторів, яка складається зазвичай просто з усіх (або деяких) фазових координат. Очевидно, що кожну координату 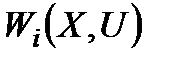або 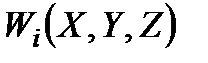потрібно збільшувати (чи зменшувати), але залишається неясним, яким саме комбінаціям значень координат вектора варто надавати перевагу, коли немає можливості (а це як правило) збільшувати або зменшувати їх одночасно.

Перехід від неповністю сформульованої моделі до звичайної, коректної, є не що інше, як процес згортання вектор-функції 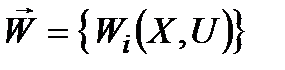( 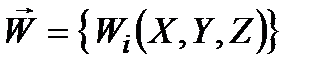) у звичайну функцію 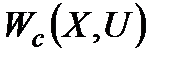або 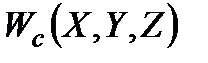. Питання про методи згортання векторного критерію є частиною більш загальної постановки задачі про методи об'єднання операцій у більш широку операцію, або, що те ж саме, про методи розбиття операції на дрібніші.

Об'єднання s операцій полягає в об'єднанні активних засобів, стратегій, неконтрольованих факторів, фазових координат, які описують хід кожної операції, і запровадженні загального єдиного критерію ефективності об'єднаної операції.

Об'єднання активних засобів − це просто додавання відповідних векторів ; для цього шляхом запровадження нульових координат (якщо це потрібно) всі вектори зводяться до одної і тої ж самої розмірності.

Об'єднання неконтрольованих факторів − векторів 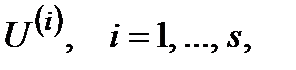відбувається ще більш формально

.

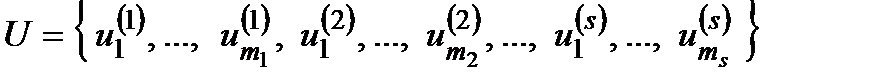Об'єднання стратегій відбувається як утворення з векторів нових векторів

,

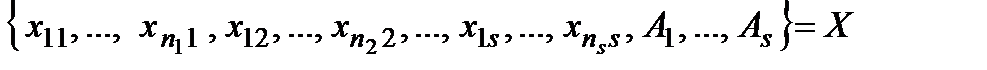де 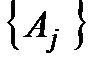− довільне розбиття сумарних активних засобів 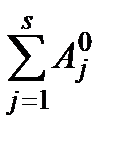за складовими операціями, які не обов'язково мають той самий запас активних засобів, що й до об'єднання. У загальному вигляді стратегію знову можна записати як .

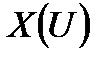Зрозуміло, що можуть бути й такі випадки, коли розподіл активних засобів при об'єднанні не може мінятись, але це нетиповий випадок свідомого об'єднання.

Можливо також, що при об'єднанні операцій активні засоби не збільшуються у порівнянні з одною операцією; у загальній схемі це рівносильне тому, що 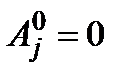для всіх 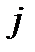, за винятком одного.

При формуванні єдиного критерію об'єднаної операції можливі дві різні ситуації.

А. Сумарний критерій має вигляд , де 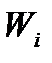- значення критерію для i-ї складової операції, тобто критерій сумарної операції є функція тільки критеріїв часткових операцій.

В. Сумарний критерій можна подати тільки як функцію фазових координат нової операції (які залежать в свою чергу від контрольованих і неконтрольованих факторів цієї операції), але не зводяться до функції часткових критеріїв.

У другому випадку об'єднана операція не має нічого спільного за своєю метою з частковими операціями, отже, є новою операцією, яка базується на активних засобах часткових операцій. Тому під об'єднанням операцій варто розуміти лише перший випадок. Звичайно, можна розглядати формально і об'єднання нескінченної кількості операцій.

Існує ряд елементарних способів об'єднання (згортання) критеріїв, тобто функцій 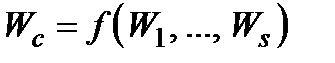, які найчастіше фігурують у практиці дослідження операцій. Опишемо деякі з них.

І. Сумування або «економічний» спосіб згортання полягає у тому, що метою об'єднаної операції є максимізація сумарного критерію вигляду

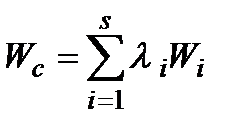(1.22)

Додатність 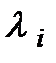, взагалі кажучи, не передбачається, хоча найчастіше 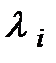невід'ємні разом з .

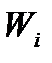За таким принципом, наприклад, утворено критерії у моделях 1.2.1, 1.2.3. Так, у моделі 1.2.1 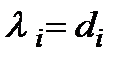, а під частковими операціями треба розуміти виробництво продукції окремими технологічними процесами. У моделі 1.2.3 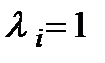, частковими операціями є призначення засобів нападу на окремих пунктах розташування засобів захисту.

Інтегральний еквівалент

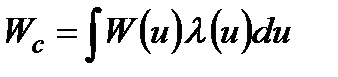(1.23)

можна одержати при згортанні критеріїв, які залежать від неперервного параметра (тобто при об'єднанні нескінченної кількості операцій).

Даний метод застосовується при осередненні критеріїв ефективності, які залежать від випадкових параметрів; тод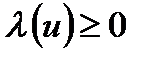і

і .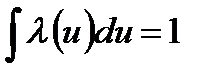

Якщо у (1.22) одна з операцій виконується завжди, а це можна характеризувати, наприклад, критерієм 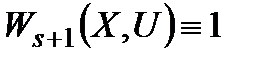, то, позначаючи 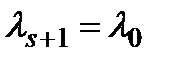, одержимо

.

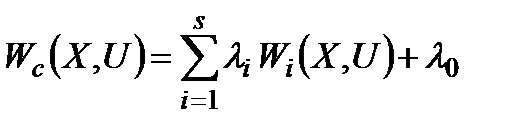Розглянутий спосіб об'єднання приводить до мети другого (кількісного) типу, навіть якщо . При об'єднанні критеріїв першого типу за цим способом для деяких складових операцій може бути висунуто вимогу обов'язкового досягнення своїх часткових цілей, тобто досягнення 1. Тоді для цих операцій необхідно покласти 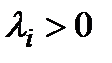і .

І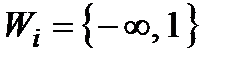І. Спосіб переходу до мети першого типу шляхом розбиття векторів 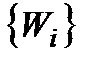на задовільні і незадовільні. Задовільними вважаються тільки вектори 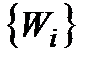, для яких

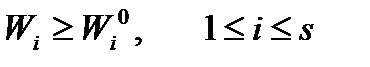. (1.24)

При цьому критерій об'єднаної операції має вигляд

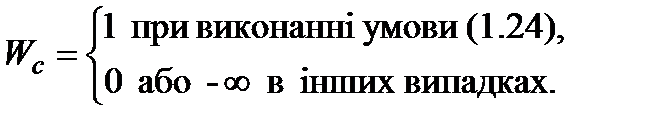(1.25)

Цей варіант може застосовуватись навіть при s=1 і означає тоді заміну мети − збільшення W на мету − досягнення нерівності .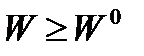

Зазвичай важко навести переконливі аргументи на користь того чи іншого вибору вектора 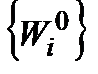, тому при застосуванні такого способу об'єднання особливо підкреслюється необхідність використання принципу свободи вибору критерію оперуючою стороною.

ІІІ. Спосіб послідовного досягнення часткових цілейВрахування виконання наступної операції починається лише тоді, коли досягнуті абсолютні максимуми критеріїв

ефективності попередніх часткових операцій. Якщо 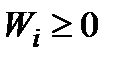, то результат об'єднаної операції можна прийняти рівним сумі досягнутих результатів врахованих операцій. Формально цей процес об'єднання (при 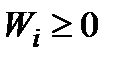) можна записати так:

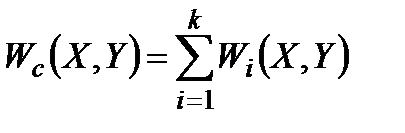, (1.26)

якщо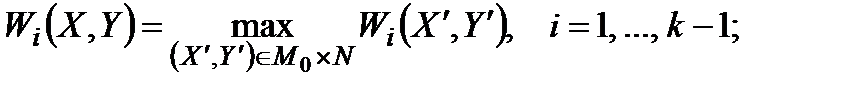

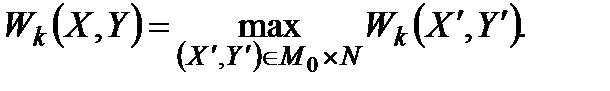
Типовим є використання такого об'єднання для випадків, коли всі частинні операції, крім, можливо, останньої, мають мету першого типу, тоді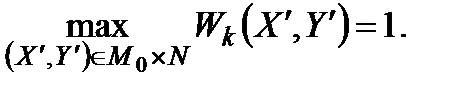

Приклад 1.2.Нехай , ,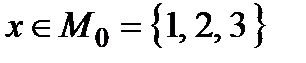

, ,

, .

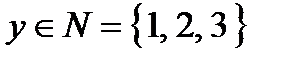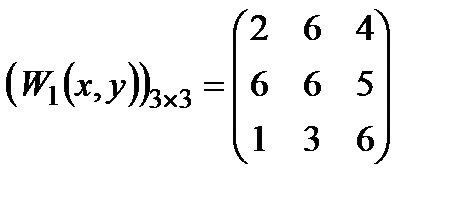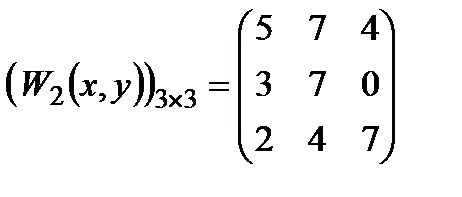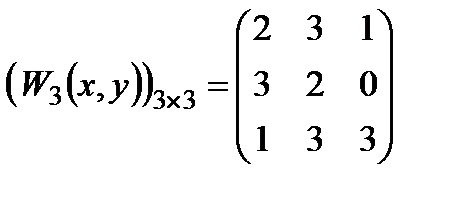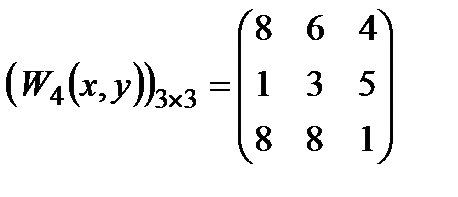Якщо оперуючи сторона прагне послідовного досягнення часткових цілей, то узагальнений критерій має вигляд

.

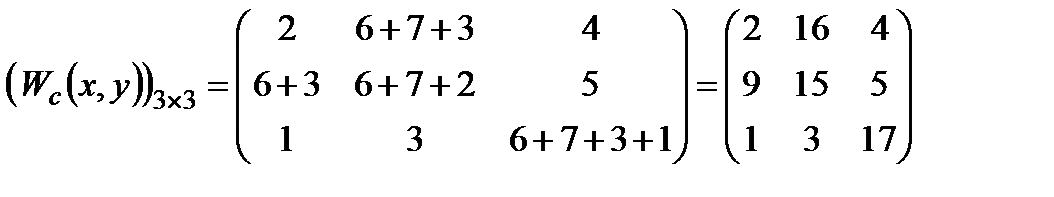Зазвичай практична реалізація такого способу об'єднання проводиться, якщо є впевненість у отриманні інформації (для своєчасного перемикання на наступну частинну операцію) про досягнення абсолютного максимум критерію попередньої операції, хоча таке об'єднання можна формально визначити і при відсутності такої інформації. Економічні операції та військові дії можуть вдало описуватись цим способом об’єднання частинних операцій. (Наприклад, організація поступового знищення сил нападу або захоплення опорних пунктів).

ІV. Логічне об'єднання цілей. Нехай критерії частинних операцій є критерії першого типу і набувають тільки значень 0 і 1. Тоді часто використовуються такі елементарні дії над цілями (критеріями):

а) метою, протилежною даній меті, називається прагнення невиконання i-ї мети; для критеріїв

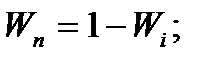(1.27)

б) сумарна мета полягяє у виконанні всіх часткових цілей (кон'юнкція)

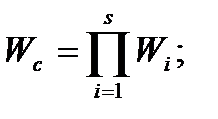(1.28)

в) сумарна мета полягяє у виконанні хоча б одної з часткових цілей (диз'юнкція)

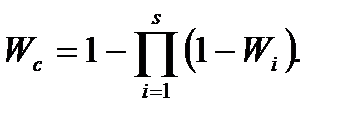(1.29)

Ці дії, як відомо, утворюють повну систему бульових операцій. Це означає, що будь-яку залежність 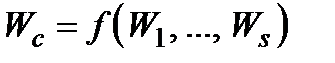, де і 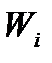набувають лише значень 0 і 1, можна подати у вигляді скінченної послідовності дій типу а), б) і в). Отже, можна повністю описати всі можливі залежності сумарного критерію від часткових критеріїв, якщо і часткові критерії, і сумарний критерій є критеріями першого (якісного) типу.

V. Узагальнене логічне згортання критеріїв. У тому випадку, коли критерії часткових операцій і /або критерій сумарної операції є критеріями другого (кількісного) типу дії попереднього пункту можна узагальнити таким чином:

замість (1.27)

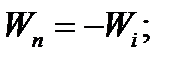(1.30)

замість (1.28)

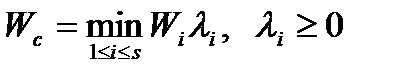; (1.31)

замість (1.29)

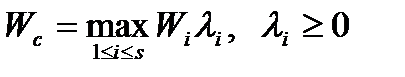. (1.32)

Ці способи об'єднання можна застосувати для критеріїв будь-якого типу.

VI. Випадкове і невизначене згортання.Сумарним критерієм оголошується той або інший частковий критерій в залежності від того, якого значення набуває неконтрольований фактор, тобто

.

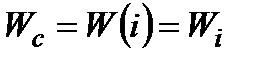У загальному випадку частинні критерії можуть визначатись неперервною випадковою або невизначеною величиною:

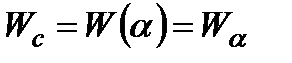(1.33)

Цей випадок є одним із шляхів проникнення випадкових і невизначених факторів у дослідження операцій і відтворює невпевненість оперуючої сторони при виборі критерію ефективності операції.

Зокрема, якщо оперуюча сторона не може точно визначити ваговий коефіцієнт 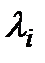частинних операцій у способах об'єднання І і V, то ці 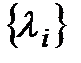і будуть тими невизначеними факторами, про які йде мова. Невпевненість оперуючої сторони при виборі критерію збільшує кількість випадкових або невизначених факторів, які не контролюються оперуючою стороною, що ускладнює вибір стратегій і зменшує їх ефективність.

При такому способі об'єднання критерії 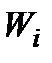стають ніби мають рівну вагу; однаково, збільшуват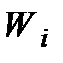и чи 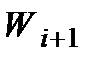, якщо збільшення однакове. Якщо і у цьому немає впевненості, то потрібно одночасно запроваджувати невизначені вагові коефіцієнти частинних критеріїв, тобто замість (1.33) писати

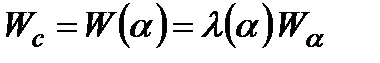(1.34)

Описані методи об'єднання критеріїв можна застосувати і у випадку неповністю сформульованої операції. Тут у ролі часткових критеріїв повинні виступати .

1.4. Повнота системи елементарних дій над критеріями (методів згортання)

Використовуючи різні комбінації описаних у попередньому параграфі методів згортання критеріїв, можна відобразити всю широту можливих однозначних залежностей критерію об’єднаної операції від критеріїв частинних операцій. Це випливає з низки результатів, наведених у книзі Гермейєра.

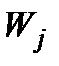Теорема 1. Якщо однозначна функція і кожний з критеріїв набувають лише скінченну кількість скінченних можливих значень, то залежність 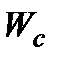від 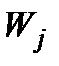може бути подана за допомогою скінченої кількості дій типу IV ( тобто (1.27)−(1.29) ), I і II ( формули (1.22) і (1.25) відповідно).

Д о в е д е н н я. Нехай 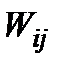− можливі дискретні значення 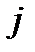-го критерію, 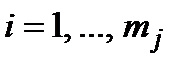, занумеровані у порядку зростання. 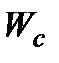також, очевидно, набуває значення із скінченної множини , .

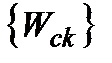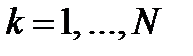Розглянемо функції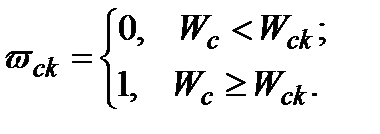

Оскільки 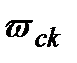є функцією від 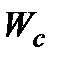, то вона є і функцією від 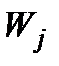. Очевидно, що

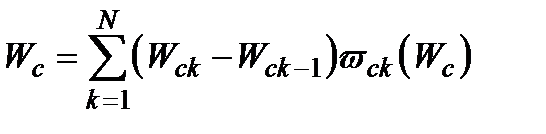, (1.35)

де 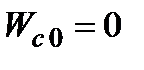. Отже, 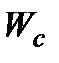утворена з 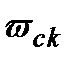способом І (1.22).

Нехай аналогічно 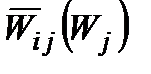визначаються за правилом

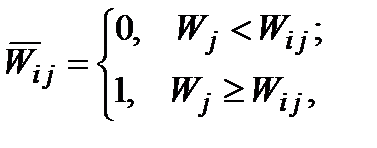
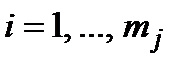. (1.36)

Таким чином, функції 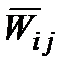утворені з 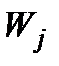, використовуючи спосіб ІІ. Крім того,

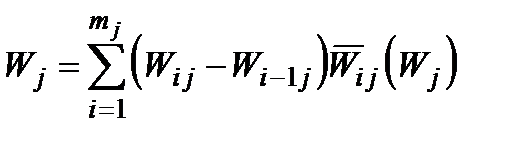(1.37)

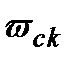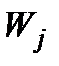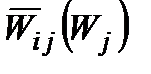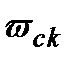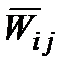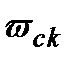Тому , які є функціями від , можуть бути записані як функції від . Оскільки і є бульовими змінними, які набувають значень з множини , то за відомою теоремою математичної логіки, залежність від 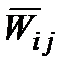може бути подана[†] як послідовність дій типу IV.

Але оскільки самі 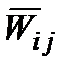виражаються через 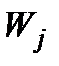за способом ІІ, а 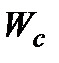− через 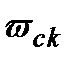за формулою (1.35), тобто за допомогою правила І, то теорему доведено. Дана теорема вичерпує всі результати щодо точного зображення залежностей 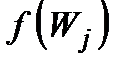у вигляді скінченної кількості елементарних дій.

Наступні теореми встановлюють лише можливість того чи іншого наближеного зображення, але з довільною заданою точністю.

Теорема 2. Нехай набуває скінченну кількість (N) значень , а 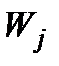нехай довільні, але обмежені. Тоді, яким би не було 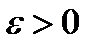, існує множина 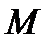векторів 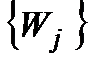і функція 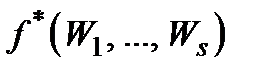, утворена за допомогою скінченої кількості дій типу І, ІІ і IV, такі, що

1) 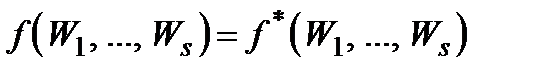, коли ;

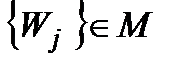2) 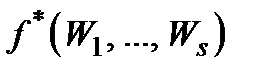пробігає всі N значень 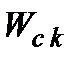, якщо 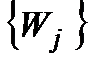пробігає значення з 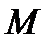, не набуваючи інших значень і при довільних ;

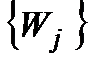3) 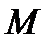утворює 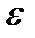-сітку на обмеженій множині всіх 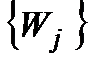, тобто для будь-якої 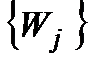знайдеться 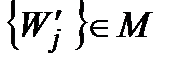, віддалена від 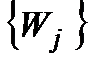не більше, ніж на .

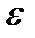Теорема 3. Якщо рівномірна неперервна на деякому паралелепіпеді можливих значень 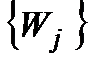, то вона з довільним ступенем точності може бути зображена у вигляді скінченої кількості дій типу І, ІІ і IV.

Оскільки дії типу V узагальнюють дії типу IV, то система дій І, ІІ і V теж є повною.

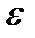Теорема 4. Якщо неперервна на області , то для будь-якого знайдеться така скінченна кількість коефіцієнтів 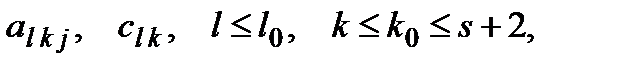що у цій області

.

Доведення теорем 2, 4 наведено у Гермейєра.

Зауваження до теореми 4.

A. У формулюванні теореми можна, звичайно, з відповідними змінами коефіцієнтів лінійних форм, брати не мінімакс, а максимін. Для цього достатньо скористатись теоремою 4 для 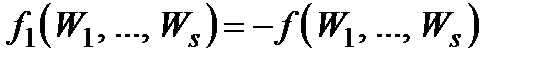і рівністю

.

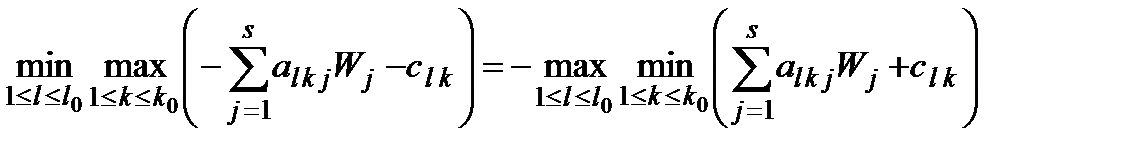В. У сучасній математиці, зокрема, у лінійному і нелінійному програмуванні і теорії ігор, велике значення мають опуклі (вгнуті) функції 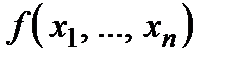, які задовольняють нерівність

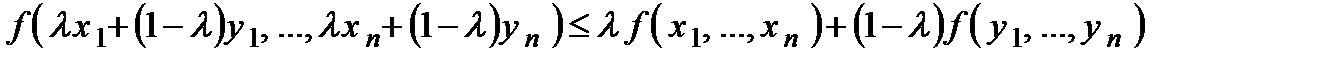
для будь-яких 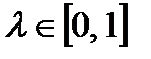. Для вгнутих функцій справджується протилежна нерівність. Можна переконатись, що функції 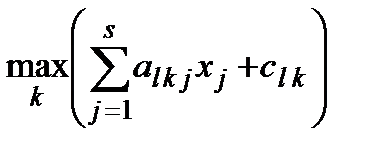опуклі. Дійсно,

[‡]

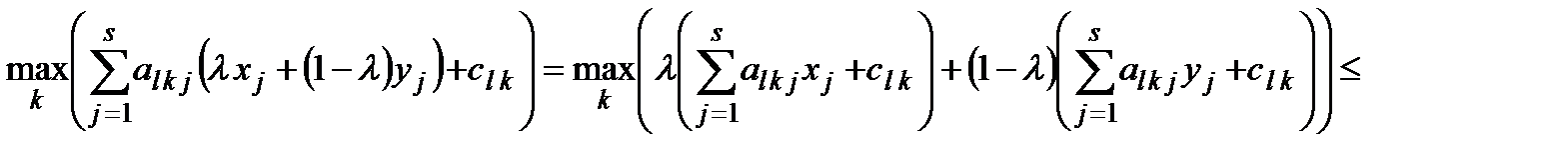
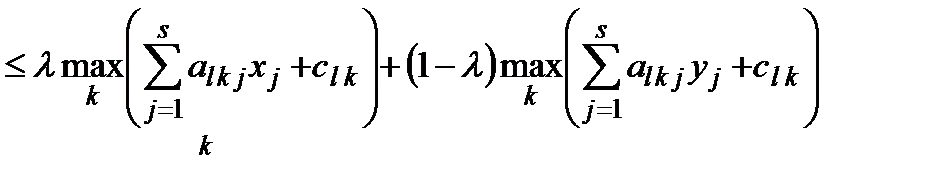Звідси випливає, що будь-яка неперервна в обмеженій області функція 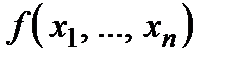з будь-яким наперед заданим ступенем точності наближено дорівнює 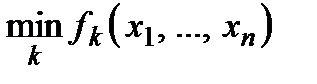, де всі − опуклі функції, тобто наближено дорівнює мінімуму, взятому за скінченною множиною опуклих функцій. Зрозуміло, згладжуючи кусково-лінійні опуклі функції, можна завжди вважати 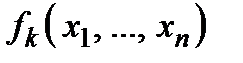досить гладкими, якщо це буде потрібно.

С. Теорема 4 може бути використана і для наближеного подання залежності критерію ефективності від контрольованих і неконтрольованих факторів. Отже, будь-який неперервний критерій ефективності можна подати як мінімакс на множині лінійних функцій або як мінімум на множині опуклих функцій.

D. Як сказано в умовах теореми, 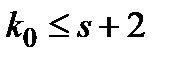, тобто не залежить від точності і області зображення. Навпаки, 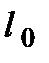сильно залежить від точності зображення 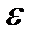і області, у якій ця точність досягається.

Якщо функція задовольняє умови Ліпшиця за всіма аргументами, то . Ця нерівність разом з нерівністю 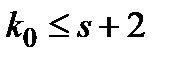досить точно описує можливий ступінь складності наближеного запису критерію за допомогою дій додавання і знаходження максимуму і мінімуму.

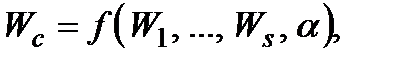Отже, теореми 1−4, показують повноту розглянутих елементарних способів об’єднання критеріїв, якщо . Якщо ж де 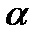− неконтрольований параметр, то використовуючи при фіксованому 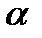наведені теореми і додаючи спосіб VI, одержимо підтвердження повноти способів об'єднання критеріїв і за наявності неконтрольованих факторів.

Деякі загальні принципи дослідження операцій (висновки до розділу 1)

1. Критерій ефективності у моделі єдиний, прагнення його збільшення є математичним еквівалентом мети операції. Але він може залежати від деяких невизначених факторів, які відображають недостатність знань про досліджувані явища або нечіткість розуміння мети оперуючої сторони.

2. В основу методів згортання вектора критеріїв при об'єднанні операцій у більш широку можна покласти операції знаходження максимуму та мінімуму результатів і сумування їх з ваговими коефіцієнтами; додавши до цього метод розбиття результатів на задовільні і незадовільні, одержимо повну систему методів згортання. Для згортання системи критеріїв якісного типу, значення яких вибираються з множини , замість максимуму і мінімуму можна застосувати логічні операції – кон'юнкцію та диз'юнкцію.

3. Оперуюча сторона має у своєму розпорядженні деяку кількість активних засобів і вибирає способи їх використання (стратегії). Метою дослідника операції є оцінка ефективності стратегій (тобто значення критерію ефективності при даному способі дій) та кількісне обґрунтування раціональних стратегій.

Величина критерію ефективності залежить також від обстановки операції – факторів, які не контролюються оперуючою стороною. За ступенем інформованості дослідника операції, неконтрольовані фактори можна розбити на такі категорії:

а) фіксовані, значення яких відомі досліднику операції;

б) випадкові, з відомими законами розподілу;

в) невизначені, для яких відома тільки їх область значень

Невизначені фактори, в свою чергу, можна розбити на «природні», причиною появи яких є недостатність знань про деякі процеси і величини, фактори що відображають нечіткість знання мети операції або критерію ефективності, і фактори, що виражають дії розумного противника, не зацікавленого у досягненні мети оперуючої сторони.

5. Оперуюча сторона може мати у момент проведення операції або навіть при її дослідженні додаткову інформацію про неконтрольовані фактори, яка невідома досліднику операції. Тому дослідник повинен, взагалі кажучи, розглядати і стратегії, які є функціями конкретного змісту цієї можливої інформації. Отже, у загальному випадку стратегія оперуючої сторони з точки зору дослідника є функція очікуваної інформації.

6. Правильно сформульована модель повинна враховувати всі суттєві неконтрольовані фактори, навіть якщо це значно ускладнює дослідження. Зокрема, майже завжди потрібно враховувати наявність неконтрольованих факторів. Особливо це суттєво у економічних і військових операціях.

7. Збільшення вектора активних засобів може тільки збільшити ступінь успішності проведення операцій при розумному його використанні. Дійсно, завжди можна просто не використовувати надлишку активних засобів. Це практично очевидне твердження може суперечити математичній моделі і навіть реальній операції, якщо у них не передбачено можливість неповного використання активних засобів, тобто створення резерву.

У математичних моделях для цього потрібно передбачити обмеження активних засобів 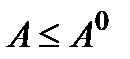(тобто 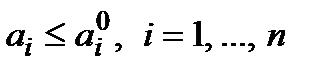), а не повне використання 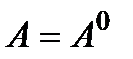. У реальній операції можливість створення резерву не завжди можна легко забезпечити.

8. Збільшення кількості стратегій також може привести до збільшення успіху.

З цієї тези випливає, що вигідно розглядати об’єднання операцій, якщо зрозуміло, як при цьому змінюється критерій ефективності. Дійсно, при цьому множина стратегій стає ширшою, ніж просто «сума» стратегій, за рахунок можливості перекидання активних засобів з одної частинної операції в іншу; отже, за рахунок цього можна одержати виграш. Саме так відбувається у дослідженнях економічних операцій, де критерій по суті не міняється (прибуток), а зміна розмірів асигнувань є суттю стратегій.

9. Збільшення інформованості оперуючої сторони (і дослідника операції) про неконтрольовані фактори може збільшити успішність дій оперуючої сторони за умови розумного використання цієї інформації.

10. При даному критерії ефективності оцінка ефективності стратегій (і вибір з множини стратегій) повинна проходити на основі одержання гарантованої (максимально гарантованої) величини критерію ефективності при даній інформованості дослідника операції і очікуваній інформованості оперуючої сторони про обстановку операції.

Отже, дослідник операції для обережності орієнтується на найгірші (для оперуючої сторони) значення неконтрольованих факторів. Така поведінка дослідника виправдана, оскільки він не має права приймати рішення, яке може бути ризикованим не лише для нього (і не стільки для нього), а для оперуючої сторони в цілому. Таких повноважень досліднику операції оперуюча сторона не надає.

Якщо ж обережність дослідника призводить в деякому розумінні до незадовільних результатів, то дослідник повинен поставити до відома оперуючу сторону, яка і приймає рішення (можливо, ризиковане).

11. Поняття гарантованого результату залежить від вибраного критерію.

Якщо, наприклад, за критерій вибрано математичне сподівання безвідмовної роботи апаратури, то гарантований результат нічого не гарантує у розумінні часу безвідмовної роботи, оскільки такий час – випадкова величина, значення якої у даній операції може виявитись як завгодно малим. Тому питання про вибір мети (і відповідно критерію) покладається на оперуючу сторону, яка, формулюючи мету, може йти на ризик, але на такий ризик не повинен йти дослідник операції.

Крім «ризику» у критерії завжди існує й елемент ризику і у прийнятті вихідних даних, наприклад, у обмеженнях невизначених факторів. Зрозуміло, що чим ширші дослідження при відповідному використанні принципу гарантованого результату, тим меншим буде елемент ризику. Тому доцільно відокремити ризик і дослідження моделі операції. Ризик залишається у виборі критерію, у формуванні моделі взагалі і в передбачуваній істинності інформації. На ці елементи ризику не може, взагалі кажучи, йти дослідник операції, діяльність якого обмежується об’єктивним і обережним дослідженням моделі.

Систематичне і послідовне застосування принципу гарантованого результату дозволяє побудувати досить струнку теорію прийняття рішень, частинним випадком якої є звичайна оптимізація, яка має місце у за умови відсутності випадкових і неконтрольованих факторів.

Наостанок коротко зупинимось на питанні про вплив часу дослідження економічних і військових операцій на побудову моделі та вигідність досліджень.

Так, дослідження військових операцій перед самими бойовими діями зазвичай присвячене вибору тактики дій з наявною зброєю. Планування таких операцій завчасно дає змогу ставити питання і про раціональний вибір типів зброї; отже, поняття стратегії при цьому розширяється і перетворюється на пошук раціонального використання асигнувань, призначених для оборони.

Тому зрозуміло, що більш раннє планування повинне приводити до успішнішої реалізації асигнувань, ніж досить випадковий вибір типів зброї і подальше дослідження способів її застосування.

З іншого боку, більш пізні дослідження проходять в умовах більшої інформованості про обстановку операції (значення неконтрольованих факторів).

Отже, потрібні дослідження обох типів. Ранні дослідження повинні дати раціональні типи і характеристики зброї, а пізніші – уточнити способи їх застосування (які як частина загального уявлення про стратегію вибирались, звичайно, і на ранньому етапі досліджень разом з вибором зброї).

Сказане повною мірою стосується і економічних досліджень, де у ролі типів зброї виступає, наприклад, обладнання, а у ролі їх використання – технологічні процеси и тип продукції.

Цікавим є той факт, що ранні більш широкі дослідження можуть виявитись більш простими і давати опорний розв'язок для подальших точніших досліджень, які можуть вестись тільки в околі цього опорного розв'язку, якщо, звичайно обстановка операції не змінилась занадто сильно.

На прикладі моделі 1 покажемо, як більш раннє дослідження може виявитись і простішим. Побудована модель відображає пізні дослідження з великою кількістю обмежень (2) за запасами сировини, обладнання тощо. Як відомо, велика кількість обмежень значно ускладнює чисельне розв’язання задач лінійного програмування.

Раннє планування технологічних процесів можна уявити як планування закупок сировини (і або обладнання). Єдиним обмеженням тоді залишається обмеження за запасом засобів, які виділяються на закупівлю сировини, що має вигляд

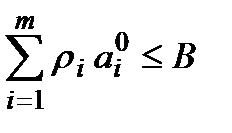
(1.38)

при збереженні обмежень (2) і критерію (3). Тут 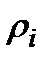− вартість одиниці і-ї сировини, 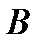− запас засобів (грошей). Тепер вже шукаємо оптимальні стратегії вигляду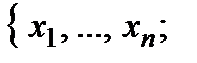 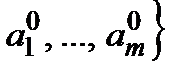. Для такої задачі оптимальні значення 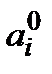і 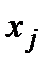повинні бути такими, що всі нерівності вигляду (2) перетворювались на рівності.

Дійсно, якщо б для деякого 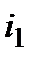у оптимальній стратегії була нерівність, то за рахунок деякого зменшення 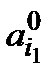можна було б збільшити всі ті 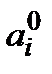, для яких виконується рівність; але тоді можна було б збільшити і всі 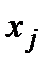, а, отже, і критерій ефективності, а це суперечить припущенню про оптимальність стратегії.

Отже, маємо

.

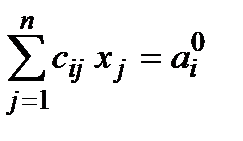Підставляючи ці вирази у (1.38), одержимо таку задачу:

знайти найбільше значення 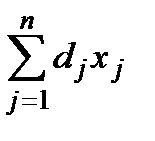при 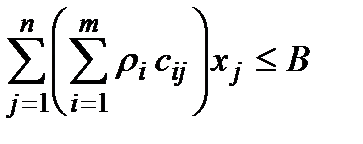; 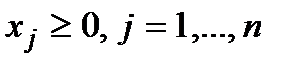. (1.39)

Використовуючи позначення, 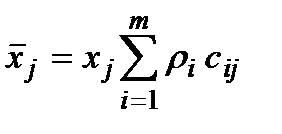, перепишемо задачу (1.39) у вигляді

; ; .

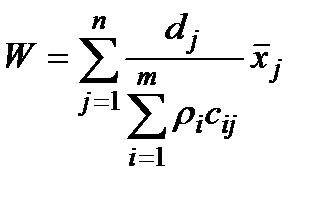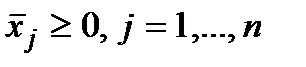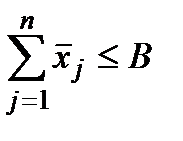Очевидно, що максимум досягається при 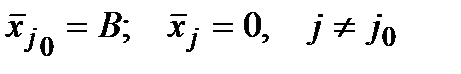, де 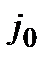− один з тих номерів, для яких

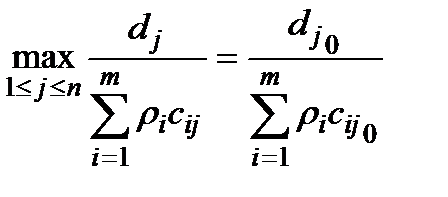. (1.40)

При цьому 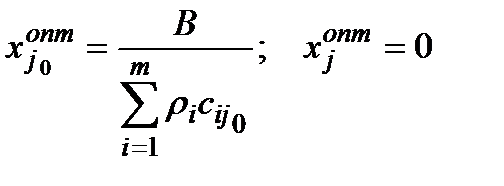при ; .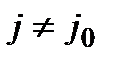

Максимум критерію дорівнює .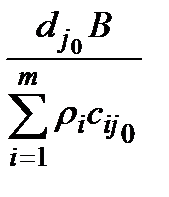

Якщо постає питання про раціональну закупівлю сировини на досить велику суму при наявності певних запасів сировини, то зберігається обмеження (1.38), але обмеження (2) потрібно замінити на таке:

(1.41)

де 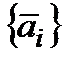− наявні запаси сировини.

Якщо закупівля проводиться на досить велику суму, то нерівності (1.41) повинні перетворюватись на рівності; тоді задача набуває вигляду

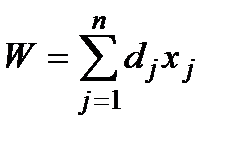при обмеженнях ; .

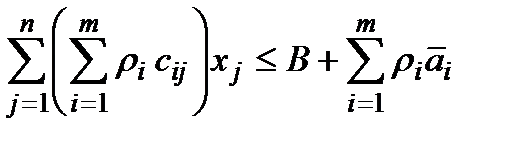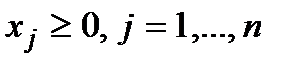Розв'язок задачі запишеться так само, як і раніше, але 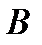потрібно замінити на 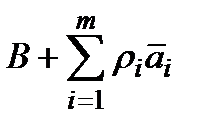і

.

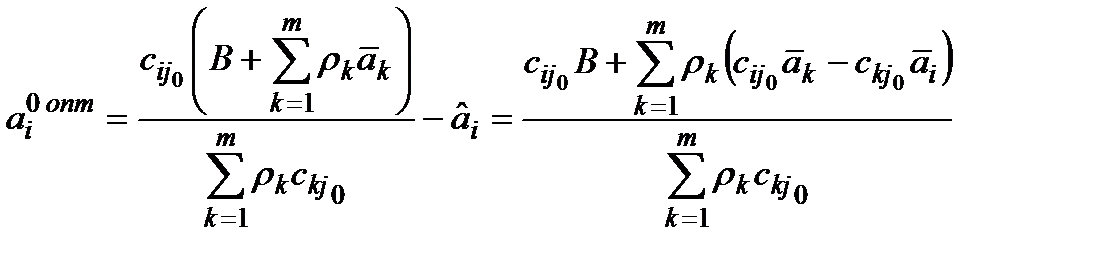Умова, достатня для того, щоб всі міркування мали сенс, має вигляд .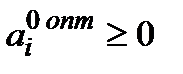

Якщо після закупівлі сировини ціни змінились у порівнянні з тими, які були в момент проведення дослідження операції, то оперуюча сторона може іноді змінити рішення про вибір ( а не 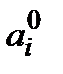). При малих змінах можна наближено залишити без змін 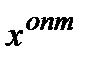; при великих варіаціях потрібно дещо змінити і 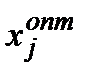. Малість цієї зміни полягає у тому, що замість одного ненульового 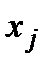тепер варто взяти два ненульових 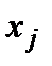, які відповідають двом найбільш ефективним 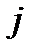при попередніх значеннях 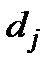. Відповідна задача лінійного програмування з двома невідомими не викликає труднощів.

Наведений приклад одночасно показує і те, що дослідження більш широкої операції, всупереч традиційному погляду, може виявитись простішим, ніж дослідження вужчої операції. Така тенденція спостерігається завжди, коли розширення операцій математично характеризується зменшенням числа обмежень щодо стратегій або активних засобів.

2. Оцінка ефективності стратегій (рішень).

2.1. Оцінка ефективності за наявності неконтрольованих факторів.

Ефективністю стратегії 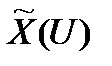називається значення критерію ефективності 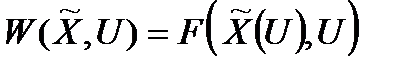для даної стратегії.

Якщо неконтрольовані фактори зводяться до фіксованих неконтрольованих факторів 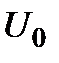, то ефективністю стратегії 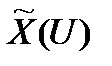буде число 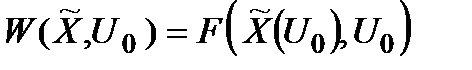, яке може бути обчислено дослідником операції. Саме це обчислення зазвичай і називається знаходженням ефективності. Цей результат гарантується наявністю інформації про .

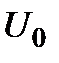У загальному випадку ефективність стратегії є, взагалі кажучи, функцією невідомих досліднику операції неконтрольованих факторів. У цих умовах дані про ефективність стратегії, які може дати (прогнозувати) дослідник, − це дані про поведінку функції .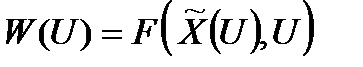

Але таке уявлення про ефективність стратегії зазвичай незручне для оперуючої сторони, для якої важливо знати, задовільна дана стратегія, чи ні. Особливо це видно для операцій з критеріями першого типу, якщо у залежності від можливих значень неконтрольованих факторів ефективність набуває обох можливих значень.

Тому бажано характеризувати ефективність стратегії одним числом. Якщо характеристику повинен дати дослідник, то така характеристика повинна базуватись на принципі гарантованого результату.

Якщо про неконтрольовані фактори нічого не відомо, крім області їх значень, то єдиною такою оцінкою ефективності буде

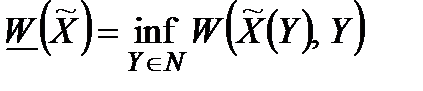, (2.1)

тобто, єдиним способом згортання критерію, який залежить від невизначеного фактора, який може дозволити собі дослідник операції, є спосіб (1.31) (частковий випадок V способу об’єднання).

Не варто думати, що така оцінка є «перестраховочною», потрібно лише при визначенні множини 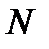врахувати всю інформацію дослідника про неконтрольовані фактори.

Дійсно, якщо вектор неконтрольованих факторів 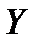є результатом дій активного противника, то вектор 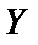буде вибиратись противником у відповідності з його метою. Якщо мета противника протилежна до мети оперуючої сторони, то він буде намагатись зменшити величину критерію 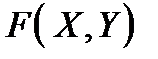, а якщо йому відома ще й стратегія 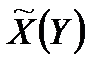, то він, звичайно, вибере 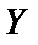таким, щоб реалізувати (2.1) або підійти досить близько до цієї величини. Тому оцінка (2.1) є точною, якщо 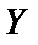вибирається противником, що має інформацію про стратегію оперуючої сторони і мету, протилежну до мети оперуючої сторони.

Нехай тепер противник має непротилежну мету, яку можна виразити у вигляді його власного критерію ефективності

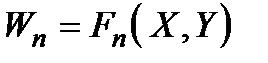. (2.2)

Якщо досліднику відомий цей критерій ефективності, то дослідник, уточнюючи вигляд множини 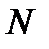, може покращити оцінку (2.1), залишаючись на позиціях гарантованого результату.

Так, якщо досліднику відомо, що противник знає стратегію 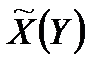, то він може виходити з того, що противник намагатиметься максимізувати функцію

,

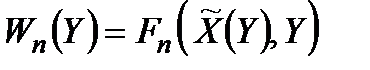тобто вибере 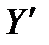так, щоб

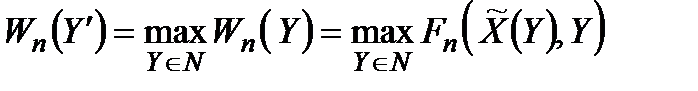, (2.3)

якщо цей максимум для нього досяжний.

Нехай 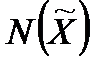− множина всіх можливих 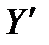, для яких виконується умова (2.3). При цьому за оцінку ефективності 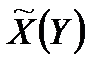дослідник операції повинен вважати

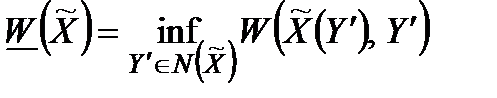(2.4)

Мінімум тут береться за всіма можливими значеннями 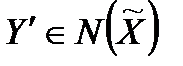, оскільки досліднику невідомі мотиви вибору одного 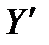з усіх, що реалізують максимум (2.3).

Застосування принципу гарантованого результату за цією невизначеністю і означає знаходження мінімуму за всіма 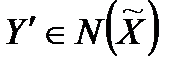. Отже, у даному випадку у (58) 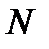потрібно замінити на .

Приклад 2.1. Нехай ,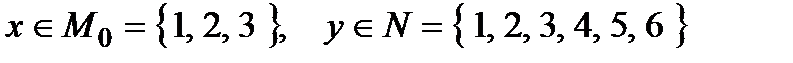

.

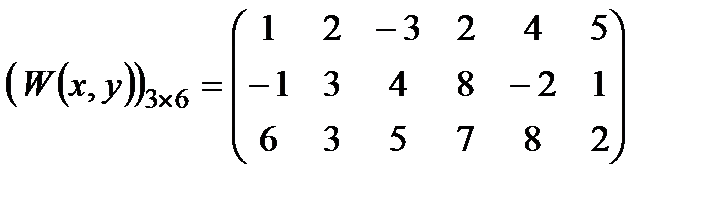Знайти оцінку ефективності стратегії 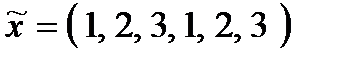у таких випадках:

а) 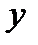− невизначений фактор, а досліджувана стратегія може бути реалізована;

в) 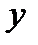− стратегія противника, який знає стратегію оперуючої сторони; мету противника задано матрицею

.

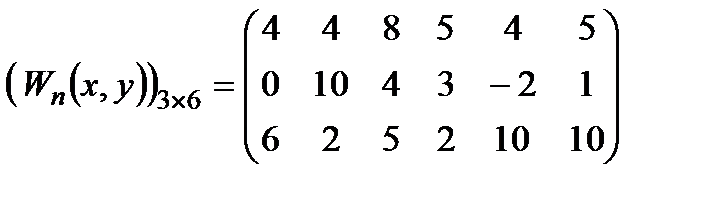Р о з в ' я з а н н я.

а) значення критерію ефективності для даної стратегії задається вектором

,

тому ;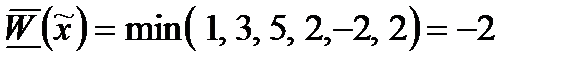

в) значення критерію ефективності противника для даної стратегії задається вектором

,

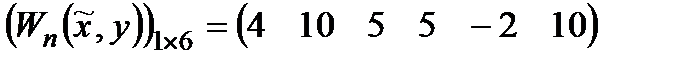тому противнику доцільно вибирати свою стратегію з множини 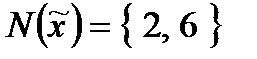, а ефективність стратегії 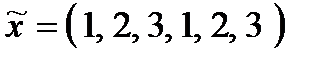дорівнює .

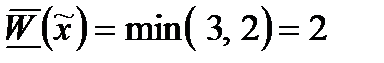Приклад 2.2. Нехай 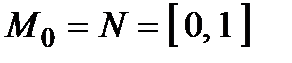, 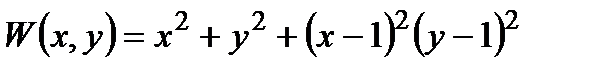. Знайти оцінку ефективності стратегії 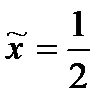, якщо

а) 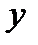− невизначений фактор, відома тільки область його значень;

в) 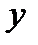− стратегія противника, який знає стратегію оперуючої сторони; мету противника задано функцією .

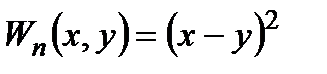Р о з в ' я з а н н я.

а) значення критерію ефективності для даної стратегії задається функцією

.

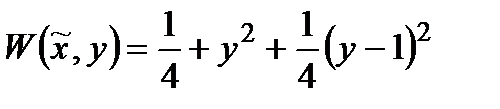За формулою (2.1) маємо ;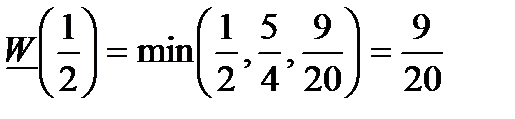

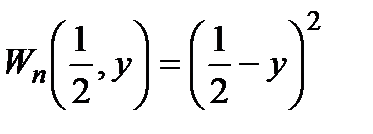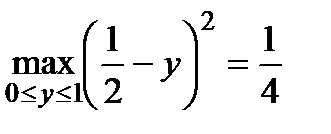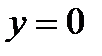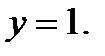в) значення критерію противника набуває такого вигляду . Максимум цього критерію досягається при і Тому .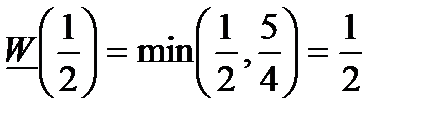

Але оцінка (2.4) буде гарантованою оцінкою тільки у тому випадку, якщо гарантовано (точно відомо досліднику або, можливо, з ризиком прийнято оперуючою стороною), що критерій ефективності противника виражається формулою (2.2), що противнику відома стратегія 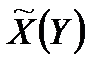і що йому нічого не заважає досягти максимуму (2.3).

Якщо хоча б одна з цих умов не виконується, то дослідник операції не має права користуватись оцінкою (2.4); це, взагалі кажучи, може спричинити помилки.

Нехай, наприклад, критерій (2.2) відомий неточно, а інші умови виконані; такий випадок можна виразити у вигляді

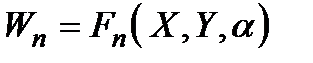, (2.5)

де 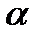− невизначений фактор, .

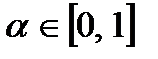Тоді противник намагатиметься одержати

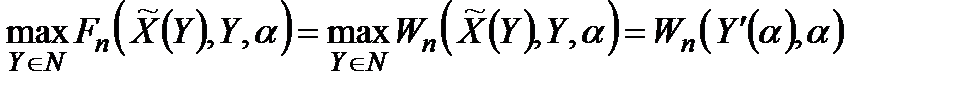
де .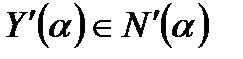

Гарантована оцінка ефективності при цьому має вигляд

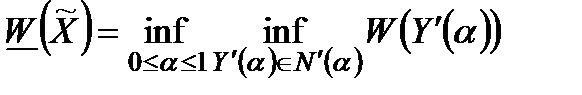(2.6)

Якщо 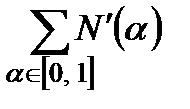містить або близько підходить до значення 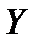, яке реалізує (2.1) , то, враховуючи (2.5)-(2.6), дослідник не одержить нічого нового у порівнянні з оцінкою (2.1).

Суттєвим є також і припущення про інформованість противника щодо стратегії .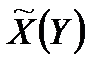

Розглянемо, наприклад, випадок, коли

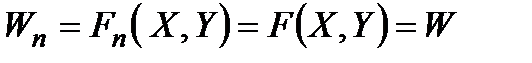, (2.7)

тобто коли «противник» має ту ж саму мету, що й оперуючи сторона; тоді обидва намагаються досягнути 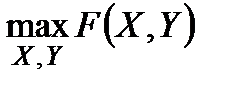. Нехай цей максимум досягається у декількох точках 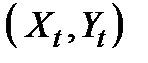, що утворюють множину 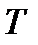, і нехай стратегія оперуючої сторони 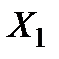не залежить від 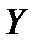; нехай, крім того, «противник» не знає цієї стратегії. Тоді вибір противника незрозумілий, і у кращому випадку можна гарантувати ефективність стратегії 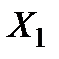у вигляді величини

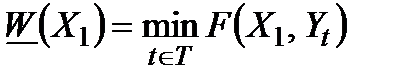. (2.8)

Ця величина може бути досить далекою від бажаного 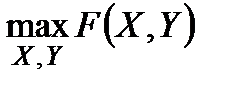і навіть збігатись з оцінкою (2.1).

Приклад 2.3. Нехай контрольований фактор 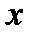і неконтрольований фактор 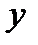− це точки з проміжку 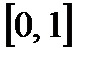, а критерій ефективності оперуючої сторони і «противника» має вигляд 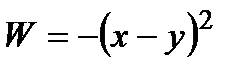, тобто обидва учасники намагаються наблизитись один до одного, але не призначили точку зустрічі (кожен з учасників не знає, куди піде інший). Тоді, очевидно, для 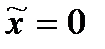за формулою (2.1) одержимо -1. Теж саме значення одержимо, застосовуючи формулу (2.8).

Отже, мало просто прагнути спільної мети, потрібно ще й обмінюватись інформацією про свої дії (стратегії), інакше спільність цілей може дати ті ж самі результати, що й їх протилежність.

Якщо немає впевненості у достатній інформованості дослідника щодо вигляду критерію противника і у інформованості противника щодо стратегії 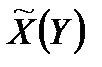оперуючої сторони, то потрібні додаткові дослідження або необхідно орієнтуватись на оцінку вигляду (2.1), враховуючи всю відому інформацію про неконтрольовані фактори 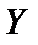. Тому у військових операціях або в умовах конкурентної економіки типовою (хоча, звичайно, не єдино можливою) повинна бути оцінка (2.1).

Це положення зберігає своє значення і для «природних» невизначеностей (у тому числі, і для невизначеностей третього типу), коли поведінку невизначеного фактора можна трактувати як дію противника з невизначеною метою, а, отже, і не поінформованого.

Сказане можна виразити і у такій формі: якщо мета противника (у тому числі «природи») невідома або немає упевненості про його інформованість щодо стратегії оперуючої сторони, то доцільно прийняти випадок протилежності мети такого противника, що є звичайно, найгіршим випадком.

Залишається зрозуміти, що дає впевненість про відсутність інформації у противника щодо стратегії оперуючої сторони. Все залежить від того, наскільки точно відома мета противника. Якщо невідома, то вибір противником значення з усієї множини 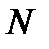залишається невизначним, тому варто користуватись оцінкою (2.1).

Таким чином, знову підтверджується доцільність оцінки (2.1) для природних невизначеностей, які не можуть бути охарактеризовані певною метою. Якщо ж мета противника відома, і він діє розумно, то при відсутності у нього інформації про 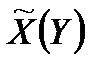він може вибрати 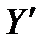з таких міркувань:

1) він вважає, що яким би не було значення , оперуючи сторона вибере так, щоб ;

2) 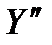тоді буде вибиратись з умови .

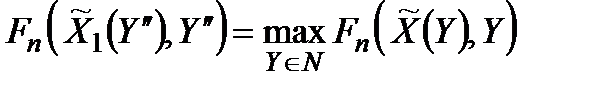Тоді, якщо 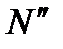є множина таких 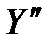, оцінка ефективності стратегії 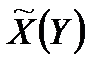буде

.

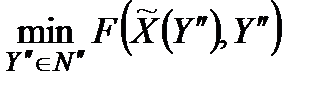Відзначаючи принципову можливість такого випадку, можна все ж таки базуватись на типовому випадку (2.1), який не спирається на сумнівні гіпотези про інформованість і поведінку противника.

Ще раз підкреслимо, що формально (2.1) охоплює всі розглянуті випадки, якщо брати нижню межу не за всіма апріорі можливими значеннями 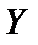, а тільки за тими з них, які відповідають даним оперуючої сторони (дослідника) щодо мети, розумності та інформованості противника.

Таким чином, ці різні випадки можна трактувати як способи обмеження множини можливих стратегій противника (множини значень невизначених факторів) на основі даних дослідника щодо мети, розумності та інформованості противника. Сказане вичерпує випадок, коли противник один, і відсутні випадкові неконтрольовані фактори.

У інших випадках іноді оцінка ефективності може бути покращена.

Коли противників багато, кожен з них має свою мету, обмін інформацією відсутній, а коаліції не укладаються, то, як показують дослідження Неша з теорії безкоаліційних ігор, можна дійсно чекати покращення результатів, але ці результати зазвичай нестійкі, і не можуть бути віднесені до категорії гарантованих. Разом з тим необхідно відзначити, що у випадку, коли немає впевненості щодо інформованості про цілі багаточисельних противників або вони можуть укладати коаліції, то найгіршим випадком для оперуючої сторони буде коаліція всіх противників, тобто по суті один противник.

Відзначимо також, що оперуюча сторона в цілому може не притримуватись принципу гарантованого результату при згортанні функції ефективності 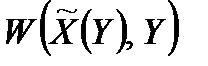у одне число. Але це буде по суті запровадження нового критерію ефективності, який утворено з старого шляхом використання способів згортання критеріїв, описаних раніше; у результаті такого згортання значення нового критерію може стати незалежним від невизначених факторів.