Модель оцінки надійності неремонтованих систем.

Нехай задано деяку систему, що складається з 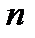агрегатів з номерами 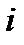, яка може перебувати тільки в одному з двох станів − працюючому і непрацюючому. Те саме стосується окремих агрегатів. Припустимо, що агрегати з'єднані послідовно, тобто вихід з ладу одного агрегату спричиняє вихід з ладу всієї системи; і навпаки, система може вийти з ладу тільки за умови виходу з ладу хоча б одного агрегату.

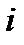Якщо позначити через момент виходу з ладу -го агрегату, то час безвідмовної роботи такої системи обчислюється за формулою

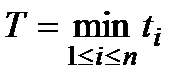. (1.8).

Критерій ефективності системи, який показує, що до моменту 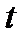система працювала або на проміжку 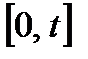вийшла з ладу, можна записати у вигляді

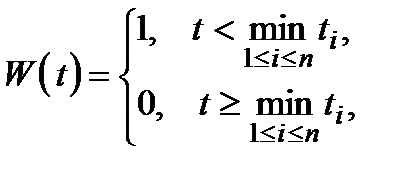(1.9)

де 0 означає, що система вийшла з ладу, 1 − працює. Часто також у ролі критерію виступає і сам час безвідмовної роботи системи.

Величини зазвичай вважаються випадковими з законами розподілу 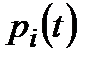, які дають ймовірність невиходу агрегату з ладу до моменту .

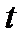Отже, тут наявні випадкові неконтрольовані фактори з відомими законами розподілу, але стратегія поки що тільки одна, оскільки конструкція системи повністю задана.

Підвищення надійності, тобто роботоспроможності системи до даного моменту 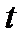або збільшення часу роботи системи 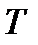досягається зазвичай за рахунок дублювання агрегатів або системи в цілому; різні способи дублювання і утворюють стратегії конструктора системи − оперуючої сторони. Для дублювання потрібно мати відповідні активні засоби, якими можуть бути або запаси (резерви) агрегатів у вигляді вектора 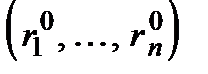або гроші на придбання 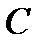при вартості агрегату .

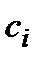Опишемо деякі способи дублювання.

А. Дублювання системи в цілому шляхом паралельного(одночасного) включення у роботу деяких систем з номерами від 1 до .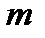

Задубльована в цілому система виходить з ладу тільки тоді, коли всі окремі системи виходять з ладу. Тоді замість (1.9) будемо мати

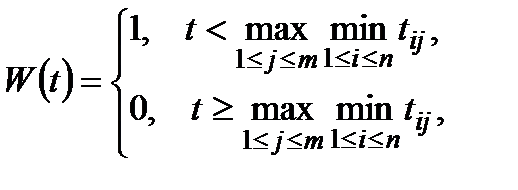(1.10)

а замість (1.8)

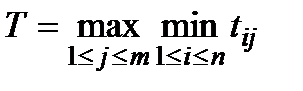, (1.11)

де 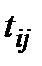момент виходу з ладу 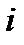-го агрегату 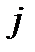-ї системи.

При цьому повинні виконуватись умови

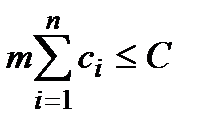(1.12)

або

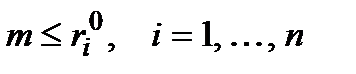. (1.13)

В. 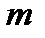-кратне дублювання системи в цілому, але шляхом «холодного резервування», коли наступна система включається в роботу у момент виходу з ладу попередньої.

У цьому випадку при збереженні умов (1.12) або (1.13) критерій ефективності системи можна записати у вигляді

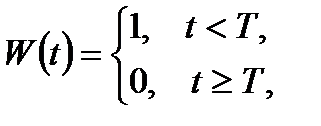(1.14)

де

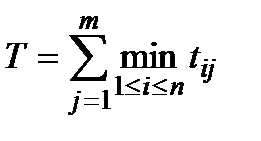. (1.15)

Стратегія у цьому випадку полягає у виборі моменту включення 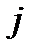-ї резервної системи, який збігається з моментом виходу з ладу 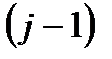-ї системи. Отже, тут у повній відповідності з загальним означенням стратегії, стратегія є функцією очікуваної оперуючою стороною інформації про неконтрольовані величини .

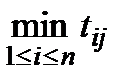С. Дублювання кожного окремого агрегату системи 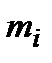разів шляхом паралельного з'єднання агрегатів, так що дубльований агрегат в цілому виходить з ладу тоді и тільки тоді, коли виходять з ладу всі агрегати, що працюють паралельно.

У цьому випадку критерій ефективності має вигляд (1.14), але

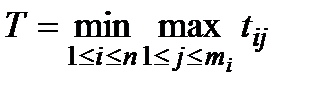(1.16)

при обмеженнях

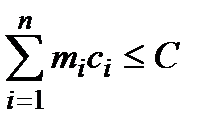(1.17)

або

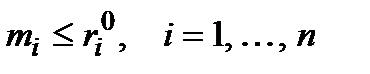. (1.18)

D. «Холодне резервування» агрегатів. У цьому випадку, очевидно,

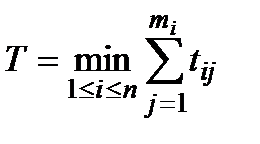(1.19)

при збереженні обмежень (1.17) або (1.18).

У випадках A−D передбачається використання інформації про всі неконтрольовані випадкові фактори .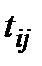

Опис можливих стратегій конструктора можна закінчити вказівкою про можливість комбінацій описаних вище способів і включення агрегатів не паралельно і не після виходу з ладу попереднього, а шляхом деякого зміщення їх у часі включення один відносно іншого.

Як вже було зазначено, 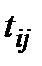− випадкові неконтрольовані фактори. Ситуація повністю описана, якщо закони розподілу 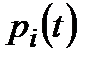відомі. Знання про 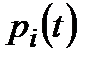еквівалентне знанню про середній час роботи агрегату

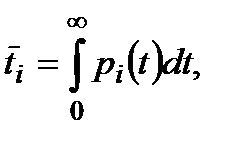(1.20)

якщо, як зазвичай передбачається у теорії надійності, 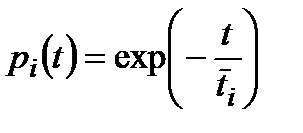. Якщо ж це не так, то знання 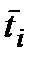і дисперсії часу роботи

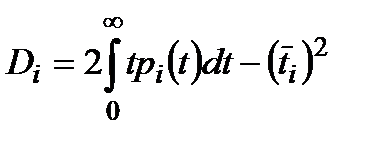(1.21)

не фіксують однозначно 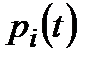. Але зазвичай експериментально можна визначити значення 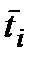, 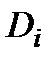і, можливо, ще декілька характеристик закону розподілу.

Тому, якщо вигляд закону 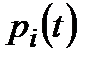апріорі зовсім невідомий або характеризується досить великою кількістю параметрів, то виникає «природна» невизначеність, яка полягає у невизначеності законів розподілу 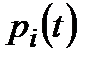, області зміни яких обмежені лише знаннями про 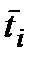і 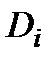, тобто рівностями (1.20), (1.21).

1.2.5. Модель для вибору дальності стрільби у дуельній ситуації.

У дуелі беруть участь два противники (перший і другий «дуелянти»). У початковий момент вони знаходяться один від одного на віддалі 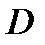. Після команди починають без зупинок наближатись один до одного, але не ближче, ніж на віддаль 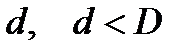. Кожен з противників може зробити один постріл у будь-який момент після початку руху. Дуель закінчується або тоді, коли обидва противники зробили по одному пострілу, або тоді, коли постріл одного був влучним. Нехай 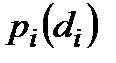− ймовірність влучного пострілу 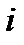-го дуелянта, якщо він стріляє з віддалі 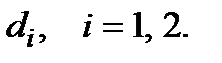Припустимо, що кожен дуелянт чує постріл противника. Першого дуелянта вважатимемо оперуючою стороною. Мета операції − влучний постріл (враження противника), критерій повинен набувати значення 1 або 0 у випадку досягнення або недосягнення мети.

Контрольованим фактором у даній операції є віддаль, з якої планує зробити постріл перший «дуелянт» 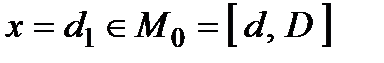. Неконтрольований невизначений фактор − віддаль, з якої планує зробити постріл другий «дуелянт» .

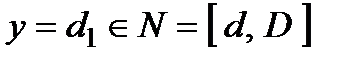Для 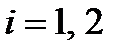розглянемо функції

Тут 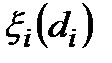при фіксованих 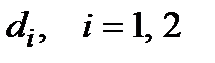, можна розглядати як випадкові неконтрольовані фактори з відомими законами розподілу.

Тоді критерій ефективності можна записати у вигляді

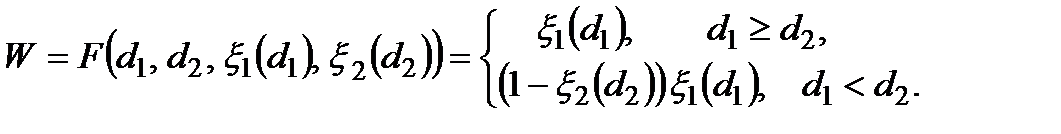
Стратегія оперуючої сторони (першого «дуелянта») характеризується константою 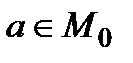і функцією 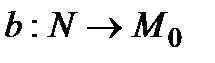. Перший дуелянт планує зробити постріл з віддалі 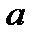за умови, що до цього моменту не надійде інформація про постріл противника (тобто перший постріл робить перший «дуелянт»). Якщо така інформація надійде (тобто 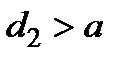), то перший дуелянт буде стріляти з віддалі 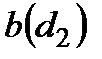. Отже, стратегія оперуючої сторони 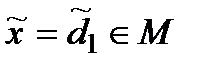має вигляд

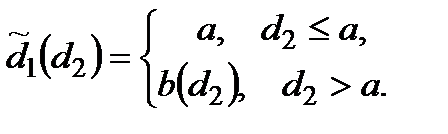
Якщо критерій ефективності повинен дорівнювати ймовірності влучного пострілу, тоді

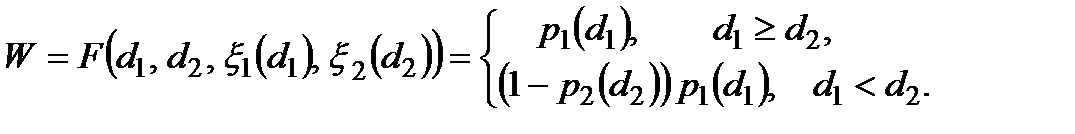
Дуельні ситуації, які характеризуються розривним критерієм ефективності, розповсюджені досить широко і не тільки у військовій справі. Вони з'являються завжди, коли момент вчинення деякої дії має принципове значення. Так, у моделі підвищення надійності використання «холодного» резервування призводить до дуельної ситуації, якщо недопустима більша за деяку величину перерва у роботі. Роль «противника» виконує природа, що «вибирає» моменти виходу з ладу агрегатів.