Модель аналізу технологічних процесів.
Нехай є 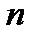 технологічних процесів, за допомогою яких виробляються деякі види продукції. Для виробництва одиниці продукції
технологічних процесів, за допомогою яких виробляються деякі види продукції. Для виробництва одиниці продукції 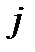 -й технологічний процес вимагає
-й технологічний процес вимагає 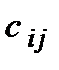 одиниць сировини
одиниць сировини 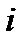 -го типу. Кількість одиниць сировини
-го типу. Кількість одиниць сировини 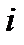 -го типу, яка є у оперуючої сторони, обмежена величиною
-го типу, яка є у оперуючої сторони, обмежена величиною 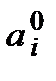 ,
, 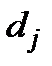 − вартість одиниці продукції, що виробляється за допомогою
− вартість одиниці продукції, що виробляється за допомогою 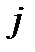 -го технологічного процесу.
-го технологічного процесу.
Нехай 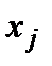 − планований обсяг випуск продукції за допомогою
− планований обсяг випуск продукції за допомогою 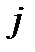 -го технологічного процесу. Контрольованим фактором є вектор
-го технологічного процесу. Контрольованим фактором є вектор 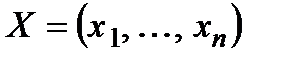 ,
,
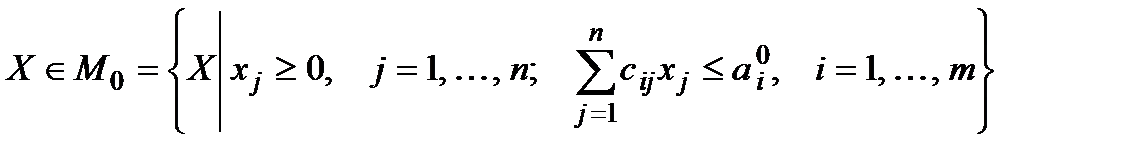 . (1.2)
. (1.2)
Критерієм ефективності вважається загальна вартість продукції, яку можна записати у вигляді
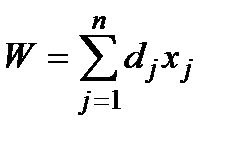 , (1.3)
, (1.3)
Максимізація 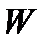 і є задача планування.
і є задача планування.
У цій моделі немає ні випадкових, ні невизначених неконтрольованих факторів, а, отже, інформованість дослідника і оперуючої сторони однакові. Активними засобами є запаси сировини, а стратегіями − вибір величин 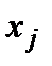 ,
, 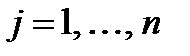 . Таким чином, у даній операції
. Таким чином, у даній операції 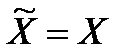 .
.
Ця модель дає типовий приклад задачі лінійного програмування.
1.2.2. Апроксимація функцій поліномами.
Нехай задано функцію 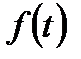 на відрізку
на відрізку 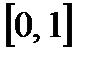 . Потрібно апроксимувати її поліномом степеня не вище за
. Потрібно апроксимувати її поліномом степеня не вище за 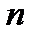 .
.
Активні засоби − степінь полінома, контрольовані фактори − коефіцієнти полінома
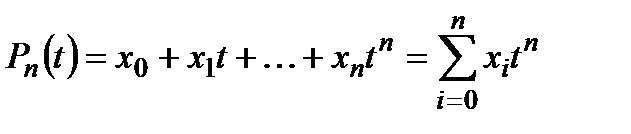 .
.
Мета операції не конкретизована, поки не вказано, що розуміти під апроксимацією. Найчастіше розглядається апроксимація у середньому, де за похибку приймається вираз
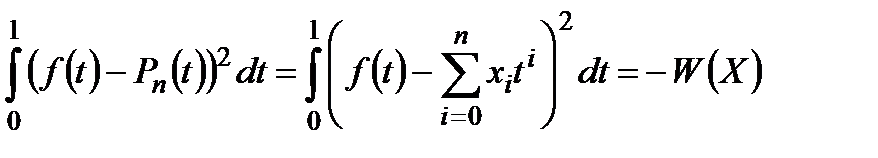 . (1.4)
. (1.4)
Мета операції − мінімізація похибки. У такій постановці задачі неконтрольовані фактори відсутні. Стратегією є вибір коефіцієнтів. Розглядаються стратегії-константи.
Але у загальнішій постановці похибкою апроксимації вважається вираз
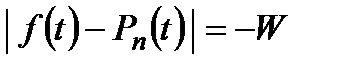 .
.
У цьому випадку значення 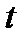 , при якому потрібно апроксимувати
, при якому потрібно апроксимувати 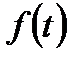 , зазвичай наперед невідоме, а, отже, є типовим неконтрольованим природним невизначеним фактором.
, зазвичай наперед невідоме, а, отже, є типовим неконтрольованим природним невизначеним фактором.
Задача про апроксимацію відомої функції поліномом може з'явитись, наприклад, для спрощення обчислень або досліджень. Але можлива також задача про апроксимацію неточно відомої функції 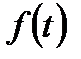 .
.
Дата добавления: 2015-02-10; просмотров: 546;
