Оптимальні стратегії.
Нехай задано множину 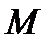 стратегій
стратегій 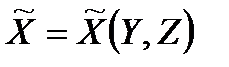 і множина
і множина  значень невизначених факторів
значень невизначених факторів 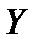 ,
, 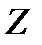 − випадкові фактори.
− випадкові фактори.
Вважатимемо, що критерій ефективності 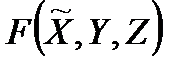 дозволено осереднювати за законом розподіл
дозволено осереднювати за законом розподіл 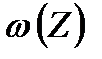 (якщо таке осереднення не дозволене, то випадкові фактори прирівнюються до невизначених); осереднений критерій позначатимемо
(якщо таке осереднення не дозволене, то випадкові фактори прирівнюються до невизначених); осереднений критерій позначатимемо 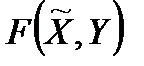 .
.
Тоді, якщо мета активного противника (якщо він є) протилежна до мети оперуючої сторони або якщо мета противника невідома, то оцінкою ефективності стратегії 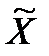 є
є
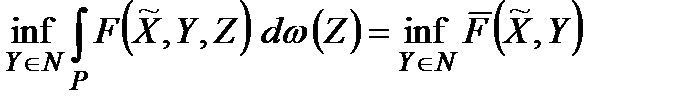 .
.
Оскільки 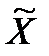 залежить, взагалі кажучи, від
залежить, взагалі кажучи, від 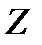 , то результат осереднення залежить від вигляду
, то результат осереднення залежить від вигляду 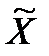 як функції
як функції 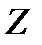 . У відповідності до двох наведених випадків порівняння стратегій можна розглядати і два поняття оптимальної стратегії.
. У відповідності до двох наведених випадків порівняння стратегій можна розглядати і два поняття оптимальної стратегії.
І. Під оптимальною стратегією (оптимальною гарантуючою) 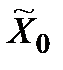 у множині
у множині 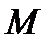 варто розуміти таку стратегію
варто розуміти таку стратегію 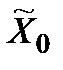 , для якої досягається максимум вказаної оцінки ефективності, тобто
, для якої досягається максимум вказаної оцінки ефективності, тобто
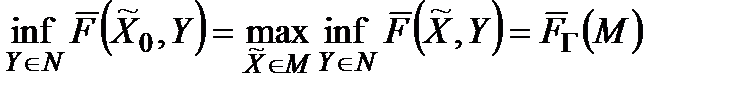 . (3.1)
. (3.1)
Сама величина 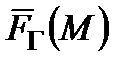 є оптимальний гарантований результат проведення операції з точки зору дослідника операції.
є оптимальний гарантований результат проведення операції з точки зору дослідника операції.
Це означення не можна замінити терміном «оптимальна пара 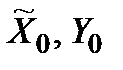 , для якої
, для якої
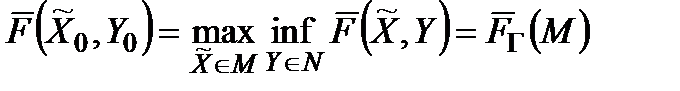 ,
,
оскільки максимін є величиною, що лежить між 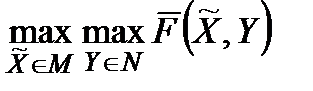 і
і 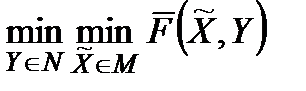 , і тому це значення досягається у певній (можливо, нескінченній) множині точок, які не мають ніякого відношення до оптимальної гарантуючої стратегії. Так, наприклад, функція
, і тому це значення досягається у певній (можливо, нескінченній) множині точок, які не мають ніякого відношення до оптимальної гарантуючої стратегії. Так, наприклад, функція 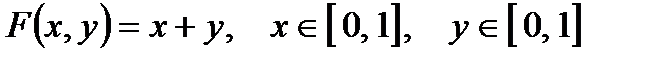 має максимін, який дорівнює 1, і єдину оптимальну гарантуючу стратегію
має максимін, який дорівнює 1, і єдину оптимальну гарантуючу стратегію 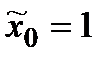 ; у той самий час всі пари, які задовольняють умову
; у той самий час всі пари, які задовольняють умову 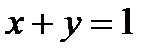 , також дають значення функції, що дорівнює максиміну, хоча відповідні
, також дають значення функції, що дорівнює максиміну, хоча відповідні  і не є оптимальними гарантуючими стратегіями.
і не є оптимальними гарантуючими стратегіями.
Якщо верхня грань 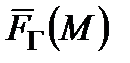 величини
величини 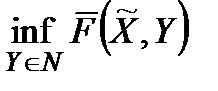 за
за 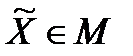 недосяжна ні для якої стратегії
недосяжна ні для якої стратегії 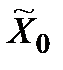 , то оптимальної гарантуючої стратегії немає, але для будь-якого
, то оптимальної гарантуючої стратегії немає, але для будь-якого 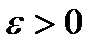 завжди існують наближено оптимальні стратегії
завжди існують наближено оптимальні стратегії 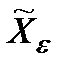 (так звані
(так звані 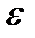 -стратегії), що задовольняють нерівність
-стратегії), що задовольняють нерівність
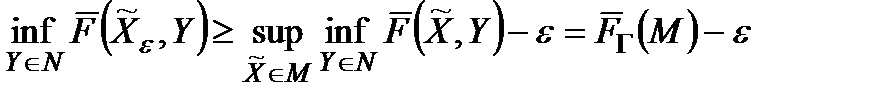 . (3.2)
. (3.2)
У випадку скінченної кількості стратегій у множині 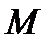 оптимальна стратегія завжди існує.
оптимальна стратегія завжди існує.
Оптимальна стратегія ( і тим паче 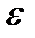 -стратегія) може бути не єдина; тоді може ставитись задача знаходження всіх таких стратегій або задача знаходження хоча б одної з них. Оскільки всі стратегії у даній операції для оперуючої сторони апріорі рівноцінні, достатньо буває знайти хоча б одну оптимальну ( або наближено оптимальну) стратегію. Потреба у знаходженні всіх оптимальних стратегій може з'явитись тоді, коли дана операція є складовою частиною іншої операції, дослідження якої передбачається пізніше.
-стратегія) може бути не єдина; тоді може ставитись задача знаходження всіх таких стратегій або задача знаходження хоча б одної з них. Оскільки всі стратегії у даній операції для оперуючої сторони апріорі рівноцінні, достатньо буває знайти хоча б одну оптимальну ( або наближено оптимальну) стратегію. Потреба у знаходженні всіх оптимальних стратегій може з'явитись тоді, коли дана операція є складовою частиною іншої операції, дослідження якої передбачається пізніше.
ІІ. Під абсолютно оптимальною (якщо вона існує) будемо розуміти таку стратегію 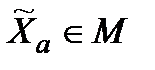 , для якої \
, для якої \
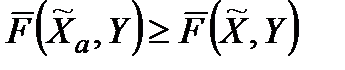
при довільних 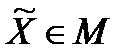 і
і 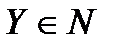 . Інакше кажучи,
. Інакше кажучи,
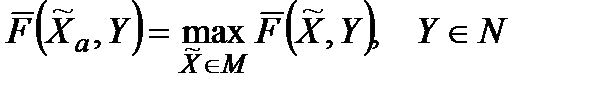 . (3.3)
. (3.3)
Під 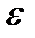 -абсолютно оптимальною стратегією варто розуміти стратегію
-абсолютно оптимальною стратегією варто розуміти стратегію 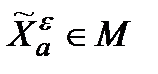 , для якої
, для якої
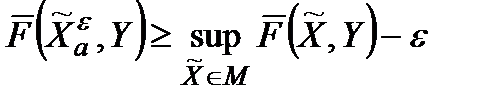 ,
,  . (3.4)
. (3.4)
Звичайно, завжди бажано знайти хоча б  -абсолютно оптимальну стратегію, а не просто оптимальну. Але це рідко буває можливо.
-абсолютно оптимальну стратегію, а не просто оптимальну. Але це рідко буває можливо.
Приклад 3.1. Нехай 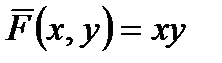 ,
, 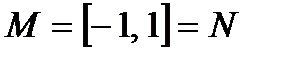 . Оптимальною стратегією є стратегія
. Оптимальною стратегією є стратегія 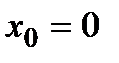 . Покажемо, що
. Покажемо, що 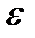 -абсолютно оптимальної стратегії при
-абсолютно оптимальної стратегії при 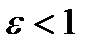 не існує. Припустимо, що це не так. Якщо
не існує. Припустимо, що це не так. Якщо 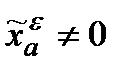 , тоді існують такі
, тоді існують такі 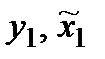 , що
, що  ,
,
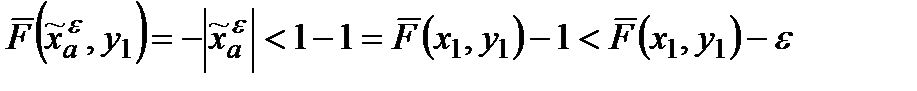 .
.
Також очевидно, що при 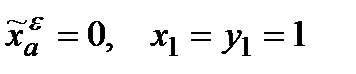 маємо
маємо 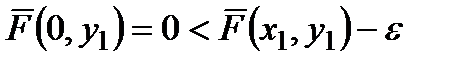 .
.
Припустимо, що у досліджуваній операції існує 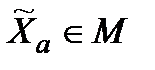 . Оцінка ефективності для
. Оцінка ефективності для  задовольняє нерівність
задовольняє нерівність
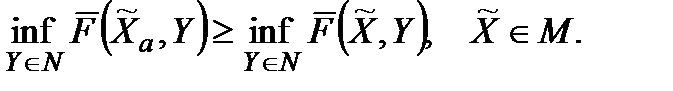
Звідси випливає, що
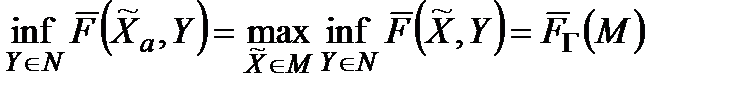 .
.
Отже, абсолютно оптимальна стратегія (якщо вона існує) є і просто оптимальною.
Аналогічне твердження справджується і для 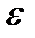 -абсолютно оптимальних стратегій. Звідси випливає, що, знайшовши всі оптимальні стратегії, серед них ми знайдемо і абсолютно оптимальну, якщо вона існує. Оскільки завжди бажано знати абсолютно оптимальну стратегію, тут ми приходимо до протиріччя з висловленою раніше тезою про відсутність необхідності знаходження всіх оптимальних стратегій. Але правильність такої тези можна відновити.
-абсолютно оптимальних стратегій. Звідси випливає, що, знайшовши всі оптимальні стратегії, серед них ми знайдемо і абсолютно оптимальну, якщо вона існує. Оскільки завжди бажано знати абсолютно оптимальну стратегію, тут ми приходимо до протиріччя з висловленою раніше тезою про відсутність необхідності знаходження всіх оптимальних стратегій. Але правильність такої тези можна відновити.
По-перше, абсолютно оптимальні стратегії можна шукати, користуючись означенням (3.3).
По-друге, якщо абсолютно оптимальні стратегії існують, то, змінюючи критерій ефективності, можна одержати операцію, у якій вони будуть просто оптимальними, а інших оптимальних не буде.
Для цього достатньо запровадити такий критерій ефективності
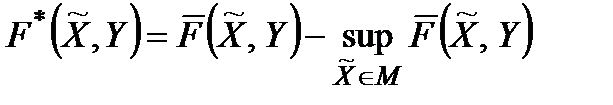 . (3.5)
. (3.5)
Оскільки завжди 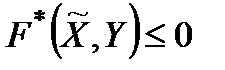 , то, очевидно,
, то, очевидно,
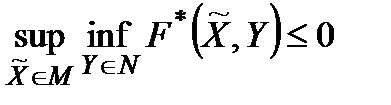 .
.
З іншого боку, також очевидно, що
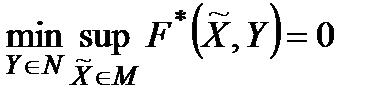 .
.
Лема 3.1. Якщо 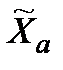 − абсолютно оптимальна стратегія для критерію
− абсолютно оптимальна стратегія для критерію 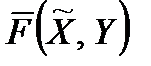 , то вона оптимальна для критерію
, то вона оптимальна для критерію 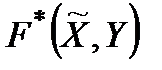 |, причому
|, причому
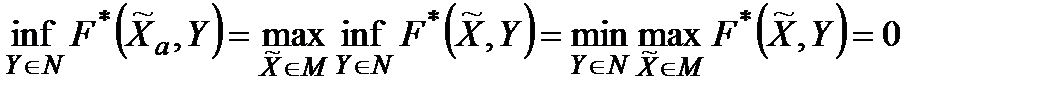 . (3.6)
. (3.6)
Навпаки, якщо справджується (3.6), то будь-яка оптимальна стратегія для 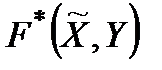 є абсолютно оптимальна стратегія для
є абсолютно оптимальна стратегія для 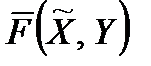 .
.
Д о в е д е н н я. Нехай 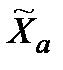 − абсолютно оптимальна для
− абсолютно оптимальна для 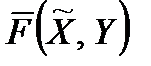 . Тоді, враховуючи (3.3), маємо
. Тоді, враховуючи (3.3), маємо 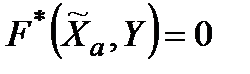 при будь-яких
при будь-яких 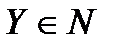 . Звідси і з відзначених вище властивостей функції
. Звідси і з відзначених вище властивостей функції 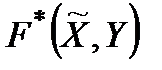 випливає правильність рівності (3.6), а, отже, і першого твердження леми.
випливає правильність рівності (3.6), а, отже, і першого твердження леми.
Нехай, навпаки, виконується рівність (3.6) і 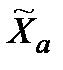 − оптимальна стратегія для
− оптимальна стратегія для 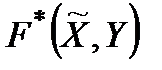 . Оскільки
. Оскільки 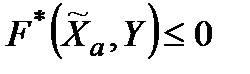 , то з (3.5) випливає, що
, то з (3.5) випливає, що 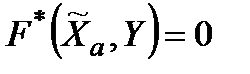 для будь-яких
для будь-яких 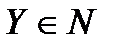 .. Але тоді
.. Але тоді 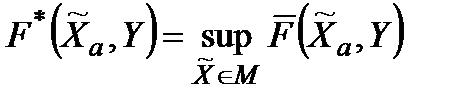 для будь-яких
для будь-яких 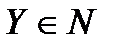 , що й доводить абсолютну оптимальність
, що й доводить абсолютну оптимальність 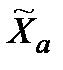 для
для 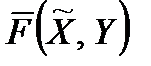 .
.
Все сказане дає змогу надалі не виокремлювати питання стосовно абсолютно оптимальних стратегій, Оскільки вони так чи інакше зводяться до питання про просто оптимальні стратегії.
Повернемось до питання про вибір оптимальних стратегій. «Найпростішим» випадком оптимального вибору є випадок, коли розглядаються стратегії-константи, тобто не очікується одержання або використання інформації про неконтрольовані фактори ( у тому числі й випадкові). Цей варіант відображає вибір стратегії для оперуючої сторони, інформованість якої протягом операції не відрізняється від інформованості дослідника операції. Оскільки такий випадок відповідає найменшій можливій інформованості оперуючої сторони, то результат проведення операції згідно з загальними принципами дослідження операцій повинен бути найменшим.
Це твердження є наслідком очевидної нерівності : якщо 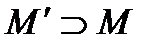 , то
, то
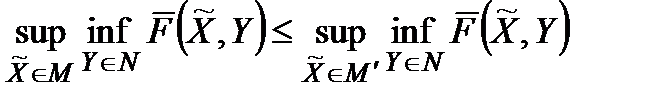 .
.
Візьмемо тепер множину  можливих значень вектор-функцій
можливих значень вектор-функцій 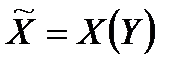 при всіх
при всіх 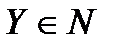 і всіх
і всіх 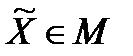 . Тоді, якщо в
. Тоді, якщо в 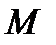 входять всі функції
входять всі функції 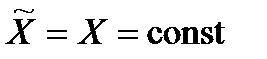 при
при 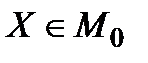
(тобто якщо  , де
, де 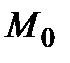 − множина стратегій-констант), то, очевидно
− множина стратегій-констант), то, очевидно
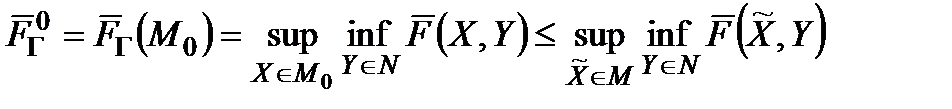 (3.7)
(3.7)
Це і є математичне вираження принципу росту результату разом з ростом інформованості оперуючої сторони.
Суттєвим тут є припущення про те, що множина 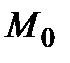 як множина стратегій, які не залежать від неконтрольованих факторів
як множина стратегій, які не залежать від неконтрольованих факторів 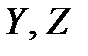 , міститься у
, міститься у 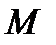 , і що, застосовуючи тільки незалежні від
, і що, застосовуючи тільки незалежні від 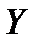 стратегії, неможливо розширити цю множину
стратегії, неможливо розширити цю множину 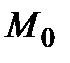 всіх можливих значень
всіх можливих значень 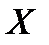 .
.
Це може відбутись, оскільки інформація має певну вартість (у сенсі активних засобів), і за рахунок її отримання у операції можуть зменшитись можливості дій оперуючої сторони, що виражаються у множині 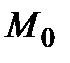 . Тому під
. Тому під 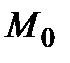 будемо розуміти саме максимально можливу множину стратегій типу
будемо розуміти саме максимально можливу множину стратегій типу 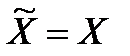 .
.
Нерівність (3.7) залишається правильною і у тому випадку, коли множина 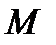 , яка не містить всіх стратегій з
, яка не містить всіх стратегій з 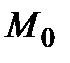 , містить все ж таки хоча б одну стратегію
, містить все ж таки хоча б одну стратегію 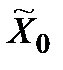 з числа оптимальних гарантуючих для
з числа оптимальних гарантуючих для 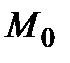 (або
(або 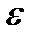 -оптимальних з відповідними змінами у нерівності (3.7) ).
-оптимальних з відповідними змінами у нерівності (3.7) ).
Оскільки множина 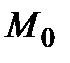 виражає межі можливих дій оперуючої сторони, то вона повинна бути відомою завжди. Зрозуміло також, що стратегії вигляду
виражає межі можливих дій оперуючої сторони, то вона повинна бути відомою завжди. Зрозуміло також, що стратегії вигляду 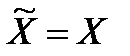 є найпростішими у реалізації стратегіями. Тому недопустимо мати результат гірший, ніж
є найпростішими у реалізації стратегіями. Тому недопустимо мати результат гірший, ніж 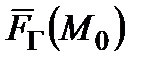 . Звідси випливає, що правильно організована множина стратегій повинна містити для обережності хоча б одну з оптимальних гарантуючих стратегій
. Звідси випливає, що правильно організована множина стратегій повинна містити для обережності хоча б одну з оптимальних гарантуючих стратегій 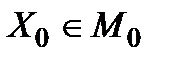 . Але таку стратегію можна знайти, тільки знаходячи максимін
. Але таку стратегію можна знайти, тільки знаходячи максимін 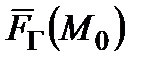 . Отже, задача знаходження
. Отже, задача знаходження 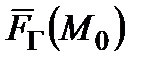 є першою і необхідною задачею на оптимум при дослідженні операцій.
є першою і необхідною задачею на оптимум при дослідженні операцій.
Приклад 3.2. Нехай 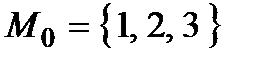 ,
, 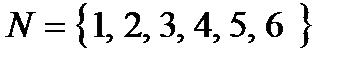 ,
,
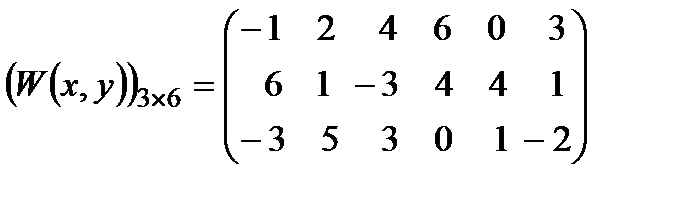 .
.
Інформаційну функцію задано у такий спосіб:
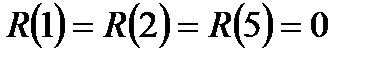 ,
, 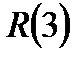 =1,
=1, 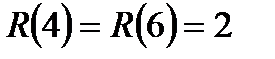 .
.
Знайти оптимальну у множині 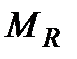 стратегію і оптимальний гарантований в
стратегію і оптимальний гарантований в 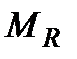 результат
результат 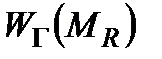 .
.
Р о з в ' я з а н н я. Множина 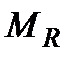 складається з 27 стратегій:
складається з 27 стратегій:
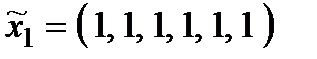 ,
, 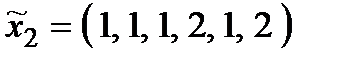 ,
, 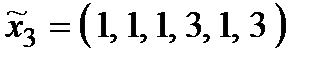 ,
,
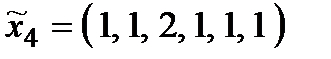 ,
, 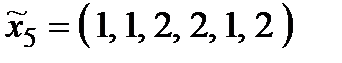 ,
, 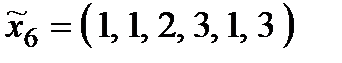 ,
,
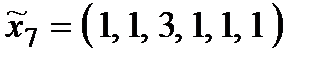 ,
, 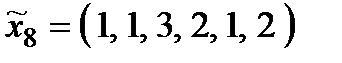 ,
, 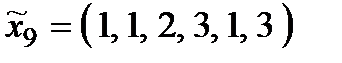 ,
,
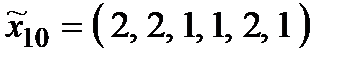 ,
, 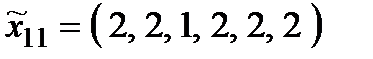 ,
, 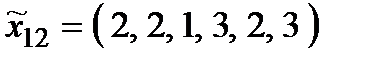 ,
,
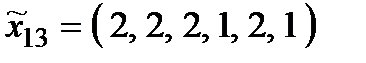 ,
, 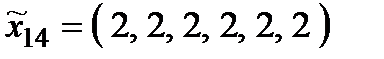 ,
, 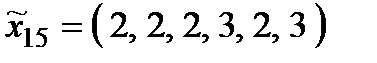 ,
,
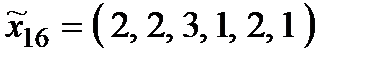 ,
, 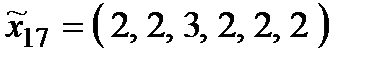 ,
, 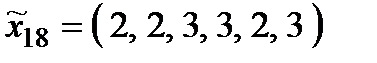 ,
,
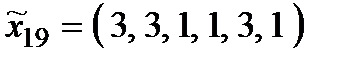 ,
, 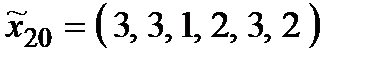 ,
, 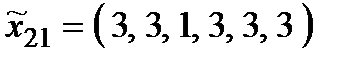 ,
,
 ,
, 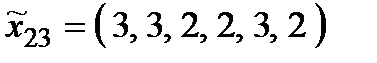 ,
, 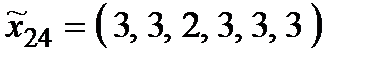 ,
,
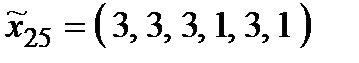 ,
, 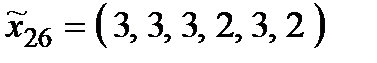 ,
, 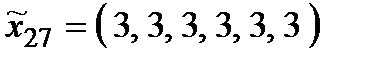 .
.
Ефективність стратегій 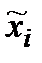 при
при 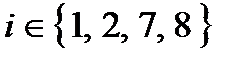 дорівнює -1, при
дорівнює -1, при 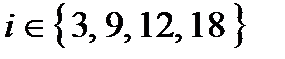 − -2, при
− -2, при 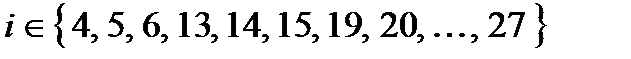 − -3, при
− -3, при 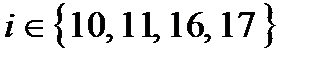 − 1, оскільки для
− 1, оскільки для 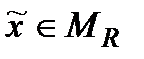

Оптимальними стратегіями є стратегії 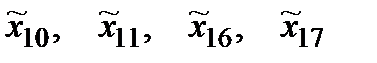 ;
; 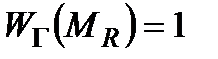 . Абсолютно оптимальних стратегій у множині
. Абсолютно оптимальних стратегій у множині 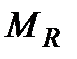 немає, оскільки при
немає, оскільки при  оптимальні стратегії дають гірший результат, ніж, наприклад, стратегія
оптимальні стратегії дають гірший результат, ніж, наприклад, стратегія 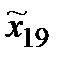 .
.
Приклад 3.3. У операції з критерієм 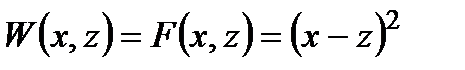
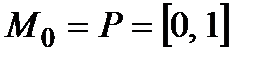 ,
, 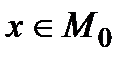 − контрольований фактор ,
− контрольований фактор , 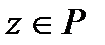 − неконтрольований випадковий фактор, рівномірно розподілений в
− неконтрольований випадковий фактор, рівномірно розподілений в 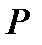 . Знайти найкращі гарантовані у
. Знайти найкращі гарантовані у 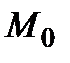 та
та 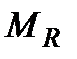 результати
результати 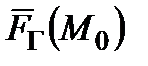 ,
, 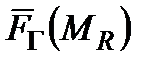 і відповідні оптимальні стратегії, якщо інформаційна функція
і відповідні оптимальні стратегії, якщо інформаційна функція
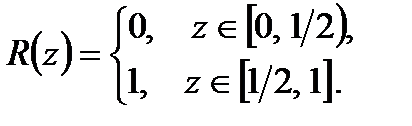
Р о з в ' я з а н н я.
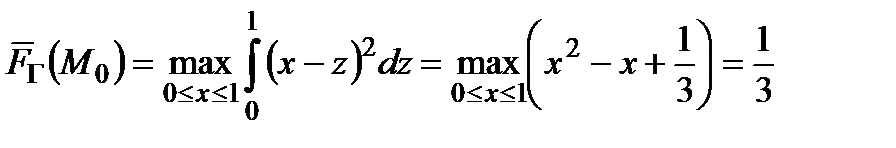 ,
,
оптимальні стратегії-константи − 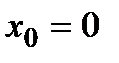 ,
, 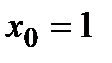 .
.
Всі стратегії 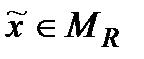 можна задати у такий спосіб
можна задати у такий спосіб
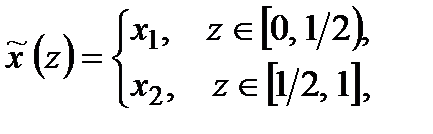
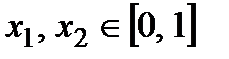 .
.
Тоді
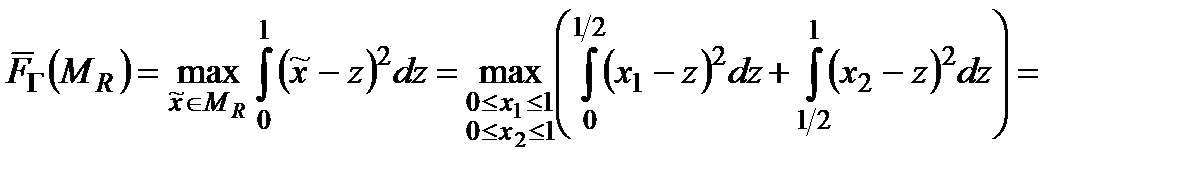
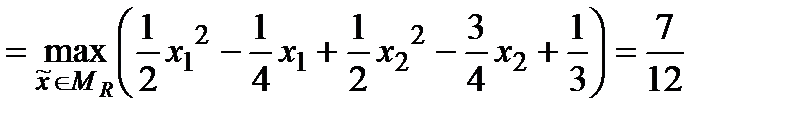 ;
;
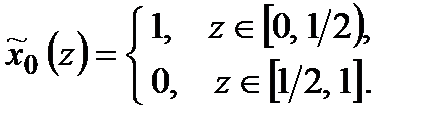
Дата добавления: 2015-02-10; просмотров: 1160;
