Критерій Гурвіца.

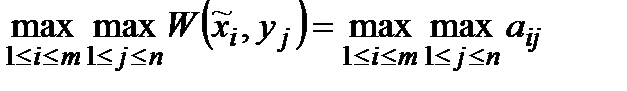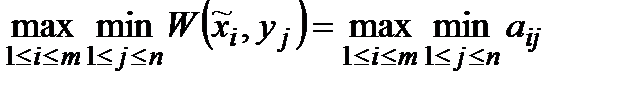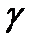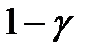Цей критерій охоплює низку різних підходів до прийняття рішень: від найбільш оптимістичного до найбільш песимістичного. При оптимістичному підході можна сподіватись на значення виграшу , а при песимістичному − . Критерій Гурвіца встановлює баланс між випадками крайнього оптимізму і крайнього песимізму, приписуючи їм вагові коефіцієнти і , де 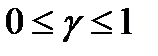(вважається, що середовище може знаходитись у найвигіднішому для оперуючої сторони стані з ймовірністю 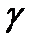і самому невигідному з ймовірністю 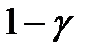). Оптимальною вважається стратегія, яка забезпечує виграш

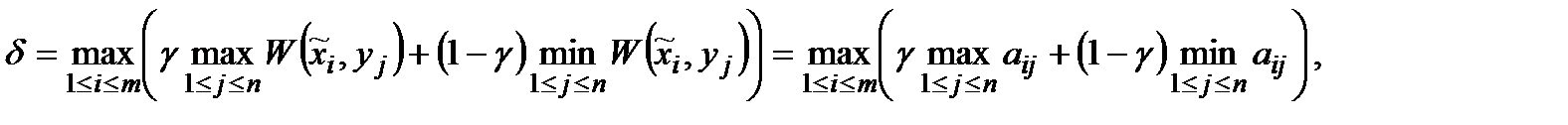
тобто

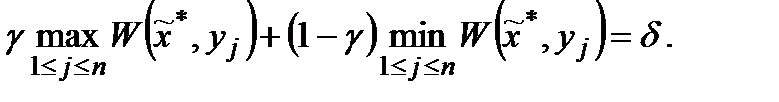
Параметр 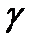є показником оптимізму: при 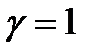критерій занадто оптимістичний, при 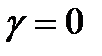дуже песимістичний. Вибір значення 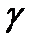залежить від схильності особи, яка приймає рішення, до оптимізму або песимізму. При відсутності яскраво вираженої схильності можна вибрати .

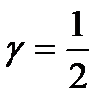Розглянемо використання даних критеріїв в умовах невизначеності у наступній практичній ситуації.

Приклад.Морське пароплавство планує організацію пасажирських перевезень на літні місяці. Кількість суден 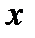, які повинні бути зафрахтовані, їх тоннаж, а також кількість екіпажів, які повинні бути набрані і підготовлені до чергової весняно-літньої навігації, є змінною величиною і визначається фактичними потребами у пасажиро- перевезеннях чергового сезону. Припустимо, що вона може набувати значень 10, 20, 30, 40 і 50 суден. Фактична потреба у пасажироперевезеннях є випадковою величиною, яка залежить від багатьох факторів. Припустимо, що пароплавство склало кошторис експлуатаційних витрат і визначило величину очікуваного прибутку від виконання перевезень в залежності від кількості зафрахтованих суден 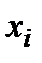і фактичних потреб у суднах для повного задоволення потреб пасажирів 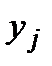. Розрахункові значення очікуваного прибутку і для всіх можливих значень 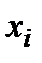та 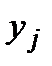наведені у таблиці

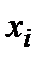
	– 48
	– 100	– 50
	– 150	– 100

Потрібно визначити оптимальну кількість зафрахтованих суден, щоб максимізувати очікуваний прибуток. Розрахуємо цю величину, використовуючи наведені вище критерії.

Критерій Вальда: , .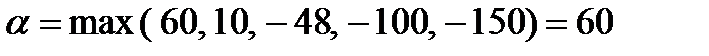

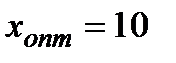Критерій Лапласа: , .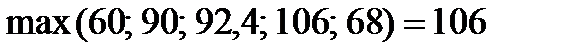

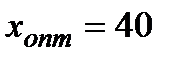Критерій Севіджа: будуємо матрицю 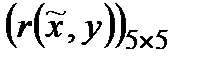, а результати заносимо у наступну таблицю

		–50	–140	–180	–280
	–50		–90	–130	–230
	– 108	–80	–40	–80	–80
	– 160	– 160			–100
	– 210	– 210	–150	–40

Обчислюємо 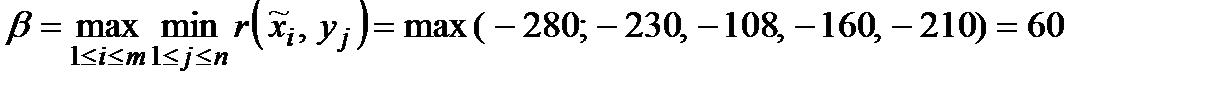, звідки .

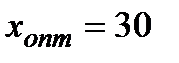Критерій Гурвіца: обчислюємо значення

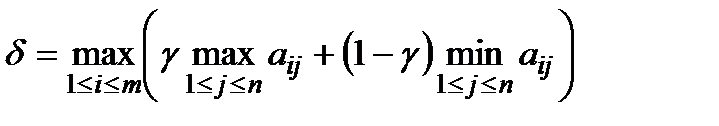
при різних значеннях .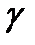

: ;

: ;

: ;

: ;

: ;

: ;

: .

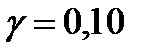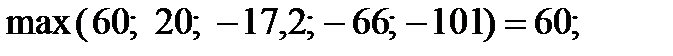
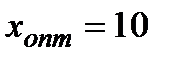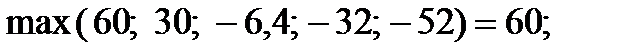
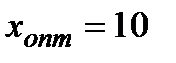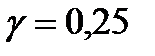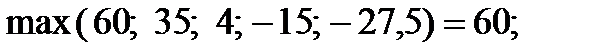
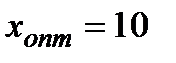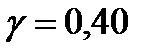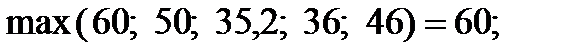
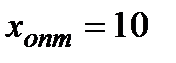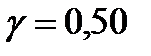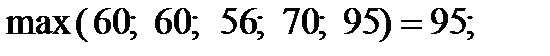
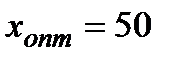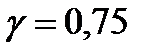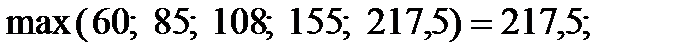
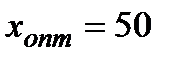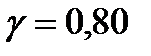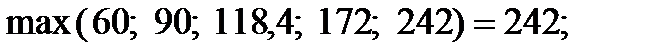
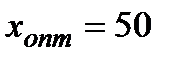Таким чином потрібно зробити вибір з таких можливостей:

А) за критерієм Вальда зафрахтувати 10 суден;

Б) за критерієм Лапласа зафрахтувати 40 суден;

В) за критерієм Севіджа зафрахтувати 30 суден;

Г) за критерієм Гурвіца зафрахтувати 10 суден, якщо керівництво порту складається з песимістів і 50 суден, якщо керівництво порту складається з оптимістів.

Якому рішенню надати перевагу? Це визначається вибором відповідного критерію в умовах невизначеності (Вальда, Лапласа, Гурвіца чи Севіджа).

Вибір критерію прийняття рішень є найскладнішим і найвідповідальнішим етапом у дослідженні операцій. При цьому не існує будь-яких загальних рекомендацій чи порад. Вибір критерію повинен робити замовник операційного дослідження на найвищому рівні ієрархії і максимально узгоджувати цей вибір з конкретною специфікою задачі та із своєю метою.

Зокрема, якщо приймається дуже відповідальне рішення, і навіть мінімальний ризик неприпустимий, то варто застосовувати критерій Вальда (принцип гарантованого результату). Навпаки, якщо деякий ризик прийнятний, і керівництво (замовник) має намір вкласти у плановану операцію певну суму (таку, щоб потім не вважати, що вкладено занадто мало), то вибирають критерій Севіджа.

При відсутності достатньої інформації для вибору критерію можливим є й альтернативний підхід, який пов'язаний з обчисленням ймовірностей успіху і невдачі на основі попереднього досвіду.

[*] Тут знову відсутня вказівка про проміжну залежність 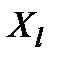від фазових координат 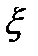і фазових координат від контрольованих і неконтрольованих факторів.

[†] Функцію 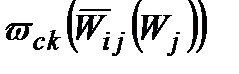завжди може бути довизначена до 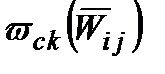для незалежних 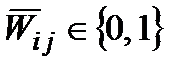. Для цього достатньо, наприклад, покласти 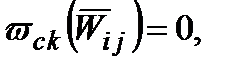якщо хоча б для одного 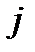вектор 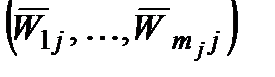не є вектор 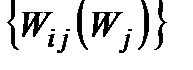. Вектор 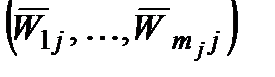, очевидно, тоді і тільки тоді, коли є вектор 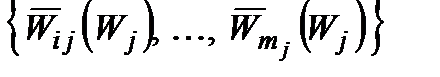для деякого 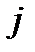, коли .

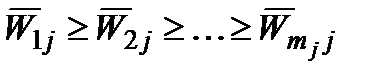[‡] Аналогічно перевіряється опуклість функції вигляду 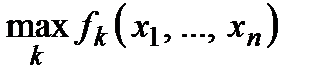, якщо всі 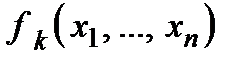опуклі. Так само 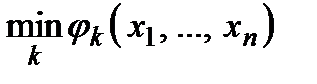вгнута, якщо вгнуті всі