Тема 1. Центральная нервная система 4 страница
Чтобы определить направление вектора ускорения Кориолиса, следует вектор относительной скорости спроектировать на плоскость перпендикулярную вектору угловой скорости переносного вращения, полученный при этом вектор следует повернуть в этой плоскости на угол 90° в сторону 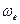
Причины появления ускорения Кориолиса
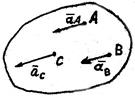
 Причиной появления ускорения Кориолиса является взаимное влияние относительного движения на переносное и переносного на относительное. В результате этого влияния переносная скорость меняет модуль и направление, а вектор относительной скорости – направление.
Причиной появления ускорения Кориолиса является взаимное влияние относительного движения на переносное и переносного на относительное. В результате этого влияния переносная скорость меняет модуль и направление, а вектор относительной скорости – направление.
Покажем это на следующем примере.

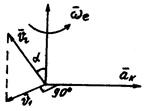
Пусть по радиусу диска, вращающегося вокруг оси, перпендикулярной плоскости диска, перемещается равномерно человек с относительной скоростью 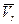 . Для какого-то фиксированного момента времени
. Для какого-то фиксированного момента времени 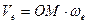 , то есть переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
, то есть переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
Пусть в момент времени 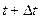 человек занимает положение М1. Очевидно, что за время
человек занимает положение М1. Очевидно, что за время 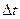 относительная скорость изменяется по направлению от
относительная скорость изменяется по направлению от 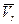 до
до 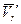 вследствие вращательного переносного движения. Вследствие относительного движения человека из точки М в точку М1 модуль переносной скорости изменился:
вследствие вращательного переносного движения. Вследствие относительного движения человека из точки М в точку М1 модуль переносной скорости изменился: 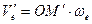 .
.
Указанные изменения вызывают' появление Кориолисова ускорения.
ЛЕКЦИЯ 9
Плоское движение твёрдого тела.
Движение твердого тела называемся плоским или плоскопараллельным, если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.

Рассмотрим произвольное плоское движение твердого тела. Пусть все точки тела перемещаются в плоскостях, параллельных плоскости  .
.
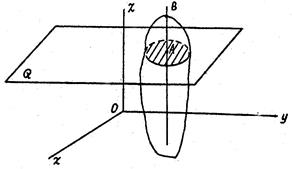
Из определенен плоского движения и из свойств твердого тела (углы между прямыми, фиксированными в твердом теле, сохраняются неизменными) следует, что любая прямая АВ проведенная в теле перпендикулярно плоскости  , будет перемещаться поступательно, то есть траектории, скорости, ускорения всех точек этой прямой будут одинаковы.
, будет перемещаться поступательно, то есть траектории, скорости, ускорения всех точек этой прямой будут одинаковы.
Таким образом, для определения движения тела необходимо знать движение лишь одной точки на каждой прямой, проведенной перпендикулярно плоскости 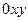 . Взяв точки в одной плоскости параллельной плоскости
. Взяв точки в одной плоскости параллельной плоскости 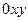 , мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью, параллельной плоскости
, мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью, параллельной плоскости 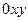 .
.
Итак, задание движения тела сводится к заданию движения одного его сечения. Поэтому будем изображать только плоскую фигуру – сечение тела и изучать движение точек этого сечения в его плоскости.
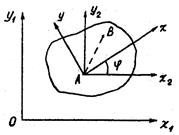
Свяжем жестко с плоской фигурой систему координат 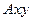 . Тогда положение системы
. Тогда положение системы 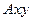 , а вместе с ней и плоской фигуры относительно
, а вместе с ней и плоской фигуры относительно 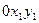 будет определено заданием координат ХА, YА точки А и углом
будет определено заданием координат ХА, YА точки А и углом  между осями АХ2 и АХ (оси АХ2 и АХ соответственно параллельны осям ОХ1 и. OY1 и перемещаются при движении плоской фигуры поступательно).
между осями АХ2 и АХ (оси АХ2 и АХ соответственно параллельны осям ОХ1 и. OY1 и перемещаются при движении плоской фигуры поступательно).
Такал образом, три функции
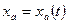
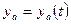
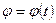
ФОРМУЛА определяют положение плоской фигуры в любой момент времени, то есть это уравнение движения плоской фигуры*
Скорости точек тела при плоском движении.
I способ
Теорема.
Скорость любой точки плоской фигуры равна геометрической суше скорости точки принятой за полюс и скорости данной точки при вращении плоской фигуры вокруг полюса.
Доказательство:
Рассмотрим плоскую фигуру. Точку А примем за полюс. Вычислим скорость точки В.
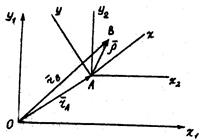
Радиус-вектор 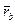 определяет положение точки В относительно OX1Y1.
определяет положение точки В относительно OX1Y1.
Радиус-вектор 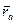 определяет положение точки А относительно OX1Y1.
определяет положение точки А относительно OX1Y1.
Радиус-вектор 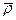 определяет положение точки В относительно AX2Y2.
определяет положение точки В относительно AX2Y2.
Очевидно 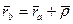
Продифференцируем по времени обе части записанного равенства
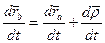 (*)
(*)
Заметим, что 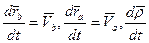 – скорость точки В относительно подвижной системы координат AX2Y2. Введем обозначение
– скорость точки В относительно подвижной системы координат AX2Y2. Введем обозначение
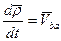 (17)
(17)
Движение тела относительно AX2Y2 представляет собой вращение тела вокруг оси AZ2 перпендикулярной плоскости чертежа. Таким образом, 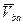 – это скорость точки В при вращении тела вокруг оси, проходящей через полюс А, то есть с учетом формулы Эйлера
– это скорость точки В при вращении тела вокруг оси, проходящей через полюс А, то есть с учетом формулы Эйлера 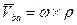 и равенство (*) принимает вид
и равенство (*) принимает вид
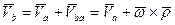 (18)
(18)
Модуль скорости 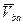 определяется следующим образом;
определяется следующим образом;
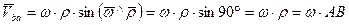
При этом вектор 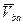 перпендикулярен
перпендикулярен 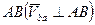 .
.
II способ
Теорема
Проекции скоростей двух точек плоской фигуры на прямую, их соединяющую – равны.
Доказательство:
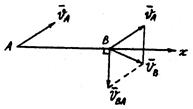
Пусть скорость точки А известна – 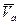 . Согласно предыдущей теореме для скорости точки В имеем
. Согласно предыдущей теореме для скорости точки В имеем 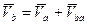 . Спроектируем обе части этого равенства на ось Х.
. Спроектируем обе части этого равенства на ось Х. 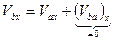 ,
, 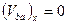 , так как
, так как 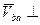 оси
оси 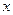 То есть
То есть
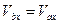 (19)
(19)
Мгновенный центр скоростей (МЦС)
МЦС называется точка плоской фигуры, скорость которой в, данный момент времени равна нулю.
Теорема
Если угловая скорость плоской фигуры не равна нулю, то МЦС существует.
Доказательство:
Пусть скорость точки. А не равна нулю, 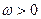 . Вычислим скорость точки Р, отстоящей от точки А на расстоянии
. Вычислим скорость точки Р, отстоящей от точки А на расстоянии 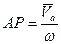 , причем
, причем 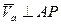 .
.
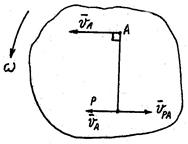
Согласно I способу 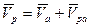 . Так как
. Так как 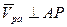 то
то 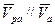 , причем
, причем 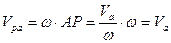 . Вектор
. Вектор 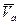 направлен противоположно
направлен противоположно 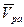 , то есть можно записать
, то есть можно записать 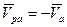
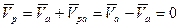 .
.
Определение скорости точки плоской фигуры с помощью МЦС
III способ.
Выберем за полюс точку Р. Тогда скорость произвольной точки А
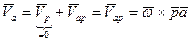 (20)
(20)
Таким образом, скорости точек тела при его плоском движении распределяются так же, как при. вращательном движении тела вокруг неподвижной оси. Роль неподвижной оси играет мгновенная ось, проходящая, через МЦС перпендикулярно плоской фигуре. Следовательно, скорости всех точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, а модули скоростей пропорциональны расстояниям от точек до МЦС.
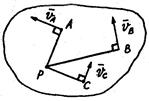
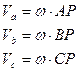
Определение угловой скорости плоской фигуры
Угловая скорость плоской фигуры определяется одним единственным способом: она равна скорости любой точки плоской фигуры, деленной на расстояние от этой точки до МЦС:
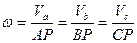 (21)
(21)
Частные случаи определения положения МЦС
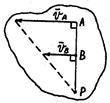
1. МЦС находится в точке пересечения перпендикуляров к векторам скоростей двух точек плоской фигуры.
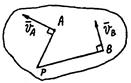
2. а) 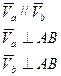
2. б) 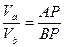
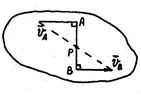
3. 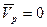
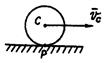
4. 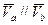 но
но 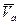 не перпендикулярна
не перпендикулярна 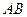
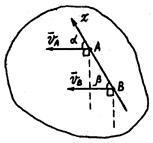
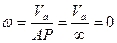
Согласно II способу определена скоростей точек
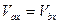 ,
, 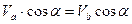 ,
, 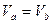 .
.
В данный момент времени скорости всех точек плоской фигуры геометрически равны. Имеем мгновенно поступательное распределение; скоростей. Угловая скорость равна нулю. МЦС находится в бесконечности.
ЛЕКЦИЯ 10
Ускорение точек при плоском движении.
Теорема.
Ускорение любой точки плоской фигуры геометрически складывается из ускорения полюса и осестремительного и вращательного ускорений во вращательном движении тела относительно полюса.
Доказательство:
В соответствии с формулой (18) имеем
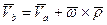
Продифференцируем последующее равенство по времени:
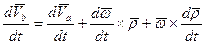
С учетом (17) это выражение принимает вид:
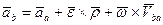 (*)
(*)
Два последних слагаемых в равенстве (*) определяют ускорение точки В при закрепленной точке А 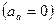 . Поэтому их сумма дает ускорение точки В во вращательное движении относительно системы AX2Y2.
. Поэтому их сумма дает ускорение точки В во вращательное движении относительно системы AX2Y2.
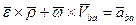
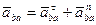 (**)
(**)
Вектор вращательного ускорения точки В во вращательном движении тела относительно полюса А направлен  ВА и определяется формулой
ВА и определяется формулой 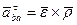
Вектор осестремительного ускорения точки В во движении тела относительно полюса А имеет направление, совпадающее с ВА, т.е. от точки, В к полюсу А, и определяется формулой 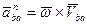 .
.
Модули этих составляющих будут
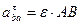
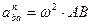
И, окончательно, равенство (*) принимает вид
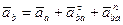 (22)
(22)
Мгновенный Центр ускорений (МЦУ)
Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой равно нуля.
Если в данный момент времени задано ускорение какой-то точки А – 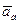 , причем
, причем 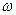 и
и 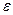 известны, то положение МЦУ определяется следующим образом.
известны, то положение МЦУ определяется следующим образом.
Проведем из точки А полупрямую AN под углом 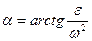 к ускорению
к ускорению 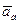 ,отсчитывая этот угол от
,отсчитывая этот угол от 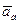 в сторону вращения плоской фигуры, если вращение является ускоренным, и против вращения, если оно замедленное.
в сторону вращения плоской фигуры, если вращение является ускоренным, и против вращения, если оно замедленное.
На полученной полупрямой отложим отрезок 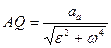 .
.
Полученная таким образом точка Q и есть МЦУ. Убедимся в том, что ускорение точки Q равно нулю.
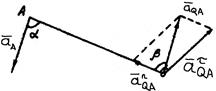
Выбрав точку А за полюс, получим
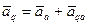
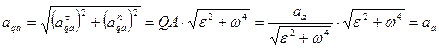
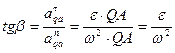
Таким образом, 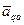 составляет с направлением QA угол
составляет с направлением QA угол 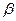 равный углу
равный углу 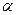 . Поэтому векторы
. Поэтому векторы 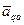 и
и 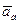 параллельны. Но в силу принятого правила отсчета угла
параллельны. Но в силу принятого правила отсчета угла 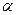 ускорения
ускорения 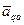 и
и 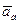 направлены противоположно.
направлены противоположно.
Учитывая, что по модулю они равны, получим 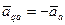 .Отсюда следует:
.Отсюда следует: 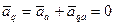
ФОРМУЛА
Таким образом, мы доказали, что точка Q – МЦУ.
Ускорение точек плоской фигуры, как ускорение
во вращательном движении вокруг МЦУ
Примем точку Q за полос. На основании (22) имеем
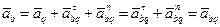 (23)
(23)
Таким образом, ускорение любой точки плоской фигуры можно определить как ускорение этой точки при вращении вокруг неподвижной оси, проходящей через МЦУ.
Частные случаи определения положения МЦУ
1. Известна точка, ускорение которой равно нулю. Эта точка и является МЦУ.
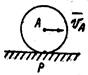
Например, качение без скольжения колеса по прямолинейному рельсу с постоянной скоростью центра С.
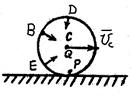
Так как 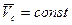 , то
, то 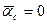 , то есть точка С есть МЦУ. Ускорение любой точки колеса, например точки В, определяется на основании (23)
, то есть точка С есть МЦУ. Ускорение любой точки колеса, например точки В, определяется на основании (23)
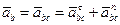
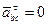 ; так как
; так как 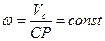
Таким образом 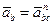
Ускорение каждой точки колеса направлено к МЦУ.
2. Равномерное вращение: 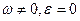 . В этом случае
. В этом случае
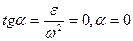
Следовательно, ускорения всех точек направлены к МЦУ, причем расстояние от точки до МЦУ определяется по формуле
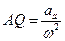
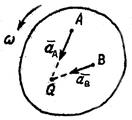
3. Момент, когда угловая скорость становится равной нулю: 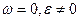
В этом случае 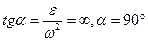 , то есть ускорения всех точек направлены перпендикулярно к отрезкам, соединявшим эти точки с МЦУ. Расстояние AQ вычисляется по формуле
, то есть ускорения всех точек направлены перпендикулярно к отрезкам, соединявшим эти точки с МЦУ. Расстояние AQ вычисляется по формуле 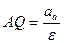 .
.
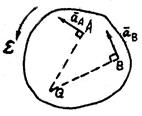
4. Момент времени, когда угловая скорость и угловое ускорение становятся равными нулю при на поступательном движении твердого тела  .
.
В этом случае ускорение любой точки равно ускорению полоса, то есть ускорения всех точек плоской фигуры геометрически равны.
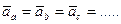
Основные способы вычисления углового ускорения
при плоском движении
1. Если известен закон изменения угла поворота или угловой скорости от времени, то угловое ускорение 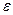 определяем путем дифференцирования, то есть
определяем путем дифференцирования, то есть
 (24)
(24)
2. Второй способ применяется в том случае, когда расстояние от точки, ускорение которой известно, до МЦС остается постоянным во все время движения плоской фигуры.
Рассмотрим, например, качение без скольжения колеса по неподвижной прямой линии.
Угловую скорость тела в этом случае можно найти по формуле (21)
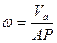
Дифференцируя 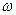 по времени, получаем о учетом, что
по времени, получаем о учетом, что 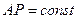 .
.
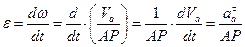 (25)
(25)
Так как в данном случае центр колеса движется прямолинейно,
то 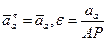
3. Третий способ применяется, когда неизвестное по модулю ускорение какой-либо точки В известно по направлению.
В этом случае, следует спроектировать обе части (22) на ось 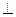 вектору ускорения точки В. Получим соотношение, из которого можно определить угловое ускорение, если другие величины входящие в это соотношение, известны.
вектору ускорения точки В. Получим соотношение, из которого можно определить угловое ускорение, если другие величины входящие в это соотношение, известны.
Определим этим способом угловое ускорение шатуна АВ кривошипно-ползунного механизма в общем виде для данного положения механизм Считаем известными угловую скорость и угловое ускорение кривошипа 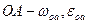 а также величины ОА, АВ, углы
а также величины ОА, АВ, углы 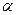 и
и 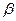 .
.
В соответствии с (22) для ускорения точки В имеем
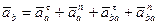 (*)
(*)
Направление векторов  показано на рисунке. Что касается векторов
показано на рисунке. Что касается векторов 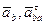 то известны только линии, вдоль которых эти векторы направлены:
то известны только линии, вдоль которых эти векторы направлены: 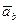 – вдоль горизонтальной прямой являвшейся траекторией точки В,
– вдоль горизонтальной прямой являвшейся траекторией точки В, 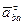 – перпендикулярно АВ.
– перпендикулярно АВ.
Зададимся произвольно направлением этих векторов вдоль указанных линий, как показано на рисунке.
Спроектируем обе части равенства (*) на оси 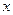 и
и 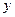 :
:
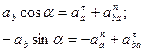
Решим полученную систему двух алгебраических уравнений относительно двух неизвестных: 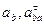 .
.
Все другие величины, входящие в эти уравнения, легко вычисляются:
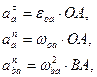
где 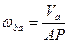
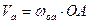 Точка Р есть МЦС звена АВ
Точка Р есть МЦС звена АВ
Из первого уравнения находим
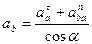
Из второго имеем
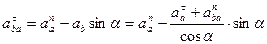
Следовательно,
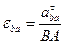 /
/
Тема 1. Центральная нервная система
Центральная нервная система человека состоит из головного и спинного мозга.
Спинной мозг внешне похож на тяж, он несколько сплюснут спереди назад. Его размер у взрослого человека составляет примерно от 41 до 45 см, а вес – около 30 гм. Он «окружается» мозговыми оболочками и располагается в мозговом канале. На всем своем протяжении толщина спинного мозга одинакова. Но он имеет всего лишь два утолщения:
1) шейное утолщение;
2) поясничное утолщение.
Именно в этих утолщениях формируются так называемые иннервационные нервы верхних и нижних конечностей. Спинной мозг делится на несколько отделов:
1) шейный отдел;
2) грудной отдел;
3) поясничный отдел;
4) крестцовый отдел.
Головной мозг человека находится в полости черепа. В нем различают два больших полушария: правое полушарие и левое полушарие. Но, помимо этих полушарий, выделяют также ствол и мозжечок. Ученые высчитали, что мозг мужчины тяжелее мозга женщины в среднем на 100 гм. Они объясняют это тем, что большинство мужчин по своим физическим параметрам гораздо больше женщин, т. е. все части тела мужчины больше частей тела женщины. Мозг активно начинает расти еще тогда, когда ребенок еще находится в утробе матери. Своего «настоящего» размера мозг достигает только тогда, когда человек достигает двадцатилетнего возраста. В самом конце жизни человека его мозг становится немного легче.
В головном мозге выделяют пять основных отделов:
1) конечный мозг;
2) промежуточный мозг;
3) средний мозг;
4) задний мозг;
5) продолговатый мозг.
Если человек перенес черепно-мозговую травму, то это всегда отрицательно сказываете как на его центральной нервной системе, так и на его психическом состоянии.
При нарушении психики человек может слышать голоса внутри головы, которые повелевают ему сделать то или иное. Все попытки заглушить эти голоса оказываются безрезультатными и в конце концов человек идет и выполняет то, что ему приказали голоса.
В полушарии различают обонятельный мозг и базальные ядра. Также всем известна такая шуточная фраза: «Напряги извилины», т. е. подумай. Действительно, «рисунок» головного мозга очень сложен. Сложность этого «рисунка» предопределяется тем, что по полушариям идут борозды и валики, которые и образуют некое подобие «извилин». Несмотря на то что этот «рисунок» строго индивидуален, выделяют несколько общих борозд. Благодаря этим общим бороздам ученые-биологи и анатомы выделили 5 долей полушарий:
1) лобную долю;
2) теменную долю;
3) затылочную долю;
4) височную долю;
5) скрытую долю.
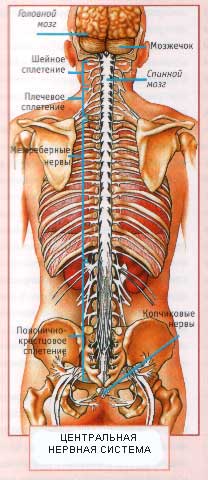 Головной и спинной мозг покрыт оболочками:
Головной и спинной мозг покрыт оболочками:
1) твердой мозговой оболочкой;
2) паутинной оболочкой;
3) мягкой оболочкой.
Твердая оболочка. Твердая оболочка покрывает снаружи спинной мозг. По своей форме она больше всего напоминает мешок. Следует сказать, что наружная твердая оболочка головного мозга – это надкостница костей черепа.
Паутинная оболочка. Паутинная оболочка представляет собой вещество, которое почти вплотную прилегает к твердой оболочке спинного мозга. Паутинная оболочка как спинного, так и головного мозга не содержит в себе никаких кровеносных сосудов.
Мягкая оболочка. Мягкая оболочка спинного и головного мозга содержит нервы и сосуды, которые, собственно, и питают оба мозга.
Возбуждение — активный физиологический процесс, которым некоторые виды клеток отвечают на внешнее воздействие. Способность клеток к возникновению возбуждения называется возбудимостью. К возбудимым клеткам относятся нервные, мышечные и железистые.
Все остальные клетки обладают только раздражимостью, т.е. способностью изменять свои метаболические процессы при действии на них каких-либо факторов (раздражителей).
В возбудимых тканях, особенно в нервной, возбуждение может распространяться по нервному волокну и является носителем информации о свойствах раздражителя. В мышечных и железистых клетках возбуждение является фактором, запускающим их специфическую деятельность, — сокращение, секрецию.
Торможение в центральной нервной системе — активный физиологический процесс, результатом которого является задержка возбуждения нервной клетки.
Вместе с возбуждением торможение составляет основу интегративной деятельности нервной системы и обеспечивает координацию всех функций организма.
Анатомической и функциональной единицей нервной системы является нервная клетка - нейрон. Нейроны имеют отростки, с помощью которых соединяются между собой и с иннервируемыми образованиями (мышечными волокнами, кровеносными сосудами, железами). Отростки нервной клетки неравнозначны в функциональном отношении: некоторые из них проводят раздражение к телу нейрона - это дендриты, и только один отросток - аксон - от тела нервной клетки к другим нейронам или органам.
Дата добавления: 2015-02-10; просмотров: 994;
