Тема 1. Центральная нервная система 2 страница
1. сила параллельна оси;
2. линия действия силы пересекает ось
Зависимость между моментами силы относительно точки и оси,
проходящей через эту точку.
Согласно определению, имеем
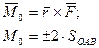
Для момента силы относительно оси 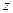 можно записать
можно записать
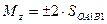
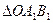 – проекция
– проекция  на плоскость перпендикулярную оси
на плоскость перпендикулярную оси  .
.
Следовательно 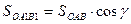 . Умножим обе части записанного равенства на 2.
. Умножим обе части записанного равенства на 2. 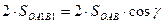 или
или
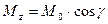 (11)
(11)
То есть, проекция вектора момента силы относительно центра на ось, проходящую через центр равна моменту силы относительной этой оси.
Аналитическое выражение моментов силы относительно оси
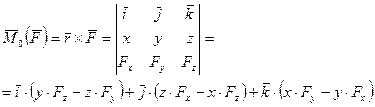 (*)
(*)
Для вектора момента силы относительно центра с учетом (II) можно записать:
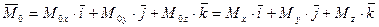 (**)
(**)
Левые части (*) и (**) равны, приравниваем правые:
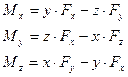
где 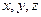 – координаты точки приложения силы.
– координаты точки приложения силы.
Главный вектор системы сил.
Главным вектором системы сил называется геометрическая сумма сил системы.
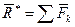
Главный момент пространственной системы сил
относительно центра и оси.
Рассмотрим систему сил ( 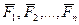 ), как угодно ориентированных в пространстве. Вычислим моменты этих сил относительно точки 0.
), как угодно ориентированных в пространстве. Вычислим моменты этих сил относительно точки 0.
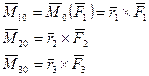
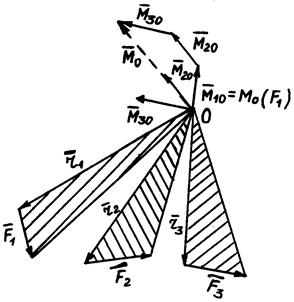
Векторы моменты 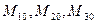 . все приложены в точке 0. Построим многоугольник векторов моментов.
. все приложены в точке 0. Построим многоугольник векторов моментов.
Замыкающая сторона этого многоугольника – главный момент относительно неподвижного центра
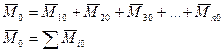 (12)
(12)
Таким образом, главным моментом пространственной системы силы относительно центра называется геометрическая сумма моментов сил системы относительно того же центра.
Главным моментом пространственной системы сил относительно неподвижной оси называется алгебраическая сумма моментов сил системы относительно той же оси
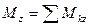
Приведение силы к заданному центру
(метод Пуансо)
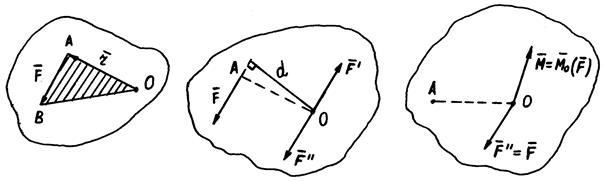
Приведём сиу 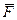 к центру 0. приложим в точке 0 систему сил
к центру 0. приложим в точке 0 систему сил  , причём выбираем
, причём выбираем
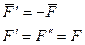
Силы 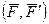 образуют пару, момент которой
образуют пару, момент которой
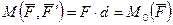
При приведении силы к заданному центру получаем в этом центре силу, геометрически равную заданной и пару сил, момент которой равен моменту силы относительно центра приведения.
Приведение пространственной системы сил к заданному центру,
Теорема.
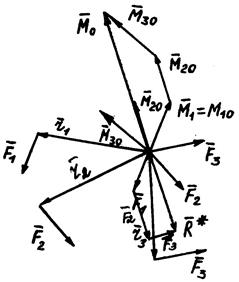
При приведении пространственной системы сил к центру всегда получим силу, называемую главным вектором системы сил, приложенную в центре приведения, и пару сил, момент которой равен главному моменту системы сил относительно центра приведения.
Доказательство:
Пусть имеем систему сил, как угодно ориентированных в пространстве (ограничимся тремя силами).
Каждую силу приводим к центру 0 на основании метода Пуансо. В точке 0 получим систему сходящихся сил 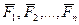 . Геометрическая сумма этих сил есть главный вектор:
. Геометрическая сумма этих сил есть главный вектор: 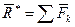
Векторы моменты 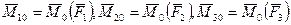 также образуют систему сходящихся векторов. Их геометрическая сумма есть главный момент системы сил относительно центра.
также образуют систему сходящихся векторов. Их геометрическая сумма есть главный момент системы сил относительно центра.
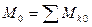
Вычисление главного вектора и главного момента
пространственной системы сил,
Главный вектор 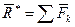
Спроектируем обе части этого векторного соотношения на оси  .
.
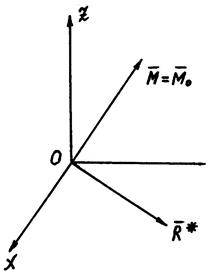
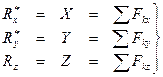 (13)
(13)
Тогда модуль 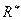 равен
равен
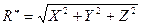 (14)
(14)
Направление 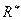 определяется направляющими косинусами:
определяется направляющими косинусами:
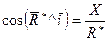 ;
; 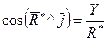 ;
; 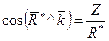 .
.
Главный момент 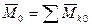 . Спроектируем данное векторное соотношение на оси
. Спроектируем данное векторное соотношение на оси 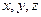 :
:
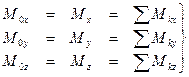 (15)
(15)
Модуль главного момента равен
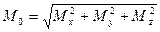 (16)
(16)
Направление определяем направляющими косинусами:
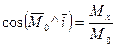 ;
; 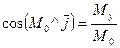 ;
; 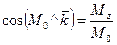 .
.
Условия и уравнения равновесия пространственной системы сил
Теорема.
Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент равнялись нулю.
Доказательство:
Достаточность.
При 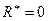 система сходящихся сил, приложенных в центре приведения 0, эквивалентна нулю, а при
система сходящихся сил, приложенных в центре приведения 0, эквивалентна нулю, а при 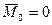 – система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
– система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
Необходимость.
Пусть данная система сил эквивалентна нулю. Тогда необходимо, чтобы 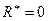 ,
, 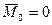 .
.
Если какое-либо из этих условий не выполняется, то система сил приводится либо к 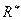 , либо к паре, момент которой
, либо к паре, момент которой 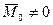 , и следовательно, не является уравновешенной, что противоречит исходной предпосылке.
, и следовательно, не является уравновешенной, что противоречит исходной предпосылке.
Получим уравнения равновесия произвольной пространственной системы сил, если 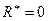 ,
, 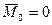 , согласно (14) и (16) :
, согласно (14) и (16) :
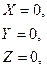
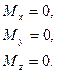
Или с учётом (13) и (15), имеем уравнения равновесия пространственной системы сил:
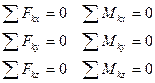 (17)
(17)
ЛЕКЦИЯ 4
Заделка.
Заделка – особый вид связи, препятствующий не только линейным перемещениям закрепленной точки тела, но и повороту вокруг этой точки.
Рассмотрим жесткую заделку левого конца балки АВ.
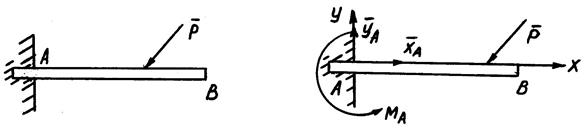
Этот конец оказывается полностью закрепленным – не возможны его вертикальное и горизонтальное перемещения, а также и поворот. Такая связь создает систему реакций, состоящую из двух составляющих  и пары, момент которой обозначен через
и пары, момент которой обозначен через  .
.
Это следует из того, что на заделанный конец балки действует распределенная нагрузка, которую можно привести к силе, приложенной в точке А, и паре сил с моментом  .
.
Следовательно, реакция заделки складывается из двух взаимно перпендикулярных составляющих 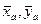 и пары, момент которой
и пары, момент которой 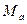 подлежит определению.
подлежит определению.
Частные случаи приведения плоской системы сил
к заданному центру.
Согласно доказанной выше теореме при приведении произвольной плоской системы сил к центру 0 получим главный вектор 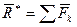 и пару силу, момент которой равен алгебраической сумме моментов сил относительно центра приведения
и пару силу, момент которой равен алгебраической сумме моментов сил относительно центра приведения 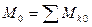 .
.
В результате приведения системы сил к данному центру могут встретиться следующие случаи:
1. 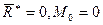 – система сил находится в равновесии.
– система сил находится в равновесии.
2. 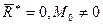 – произвольная плоская система сил приводится к паре, момент которой равен главному моменту ФОРМУЛА.
– произвольная плоская система сил приводится к паре, момент которой равен главному моменту ФОРМУЛА.
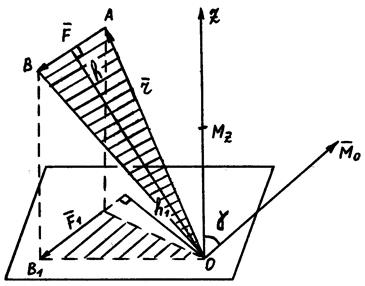
3. 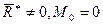 – произвольная плоская система сил приводится к равнодействующей, линия действия которой проходит через центр приведения 0.
– произвольная плоская система сил приводится к равнодействующей, линия действия которой проходит через центр приведения 0.
4. 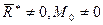 . Докажем, что в »том случае система сил также приводится к равнодействующей
. Докажем, что в »том случае система сил также приводится к равнодействующей
Силы пары с моментом 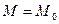 выберем следующим образом: будем считать их по модулю равными
выберем следующим образом: будем считать их по модулю равными 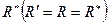 и одну из сил пары
и одну из сил пары
приложим в точке 0 (рис. 2). Плечо пары 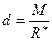 . Система сил
. Система сил 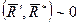 и, согласно аксиоме 2, ее можно отбросить (рис. 3). Следовательно, система сил приводится к равнодействующей, геометрически равной главному вектору
и, согласно аксиоме 2, ее можно отбросить (рис. 3). Следовательно, система сил приводится к равнодействующей, геометрически равной главному вектору 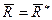 . Причем линия действия равнодействующей проходит через точку К, отстоящую от точки 0 на расстоянии
. Причем линия действия равнодействующей проходит через точку К, отстоящую от точки 0 на расстоянии 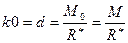
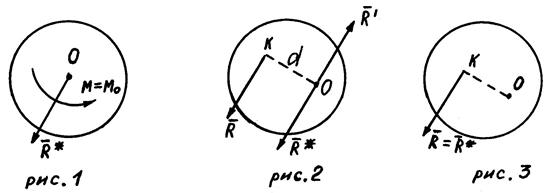
Теорема Вариньона,
Момент равнодействующей силы относительно любого центра равен алгебраической сумме моментов составляющих сил относительно того же центра.
Доказательство:
(смотри рис. 3)
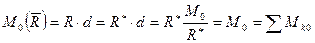
Главный вектор и равнодействующая.
Главный вектор, как геометрическая сумма сил, приложен в центре приведения, но не имеет строго определенной линии действия; он эквивалентен системе сил в совокупности с главным моментом.
Равнодействующая имеет строго определенную линию действия, она одна эквивалентна системе сил.
Условия и уравнения равновесия плоской системы сил.
Для равновесия плоской системы сил необходимо и достаточно, чтобы 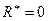 и
и 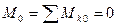 . Но
. Но 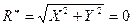 , тогда, когда
, тогда, когда 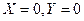 . Или, уравнения равновесия имеют вид:
. Или, уравнения равновесия имеют вид:
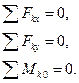 (18)
(18)
Другие формы уравнений равновесия:
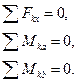 (19)
(19)
Точки А и В не должны лежать на прямой, перпендикулярной оси 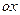
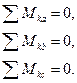 (20)
(20)
Точки А, В, С не лежат на одной прямой.
Плоская система параллельных сил.
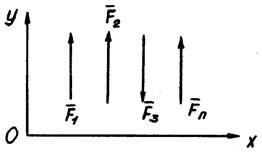
Уравнения равновесия (18) и (19) принимают вид:
 (21)
(21)
и  (22)
(22)
Прямая АВ не параллельная линии действия сил, то есть оси  .
.
Статически определенные и статически неопределенные задачи.
Статически определенными задачами называются задачи, в которых число неизвестных реакций приложенных связей не превышает числа уравнений равновесия, содержащих эти реакции.
Статически неопределенными задачами называются задачи с числом неизвестных, превышающих число уравнений равновесия сил.
Распределенные нагрузки.
Кроме сосредоточенных сил встречаются нагрузки, распределённые вдоль данной поверхности по тому или иному закону. Величина силы, приходящейся на единицу длины загруженного участка, называется интенсивностью 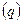 . Размерность
. Размерность 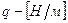 .
.
Равномерно-распределенная нагрузка вдоль отрезка прямой.
При статических расчетах эту систему сил можно заменить равнодействующей 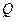 .
. 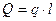 .
.
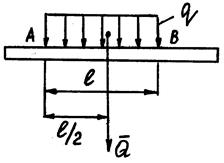
Линия действия равнодействующей 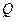 приложена в середине отрезка АВ.
приложена в середине отрезка АВ.
Неравномерно - распределенная нагрузка
(силы распределены вдоль отрезка прямой по линейному закону).
Равнодействующая 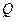 таких сил
таких сил 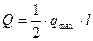
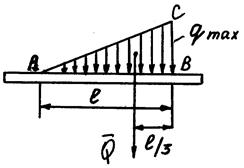
Линия действия  проходит через центр тяжести треугольника АВС.
проходит через центр тяжести треугольника АВС.
Силы, распределённые вдоль отрезка прямой
по произвольному закону
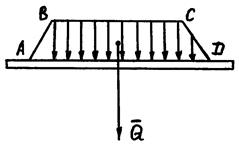
Если закон распределения нагрузки произвольный, то величина равнодействующей пропорциональна площади ABCD, 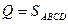 ; линия действия равнодействующей проходит через центр тяжести фигуры ABCD.
; линия действия равнодействующей проходит через центр тяжести фигуры ABCD.
Равновесие составной конструкции,
Рассмотрим задачу о нахождении опорных реакций трёхшарнирной арки, состоящей из двух частей I и II, соединенных шарниром С.
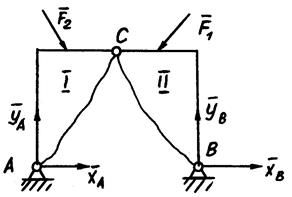
Система сил, действующих на арку – произвольно-плоская. Для нее можно составить три уравнения равновесия, неизвестных четыре – 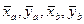 . Задача статически неопределенная.
. Задача статически неопределенная.
Чтобы сделать ее статически определенной, следует расчленить конструкцию, действие отброшенных частей заменить силами, удовлетворяющими условию:
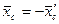
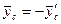
Кинематика.
ЛЕКЦИЯ 5
Кинематикой называется раздел механики, в котором изучается движение материальных точек и тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Мы будем изучать простейшую форму движения – механическое движение, то есть происходящее во времени изменение положения одного тела относительно другого, с которым связана система координат, называемая системой отсчета.
Эта система может быть как движущейся, так и условно неподвижной.
Рассматривая движение, мы связываем изменение положения тела или точки с течением времени.
При изучении движения всегда устанавливаем начало отсчета времени 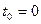 .
.
Непрерывную кривую, которую описывает точка при своем движении, называют траекторией.
Если траектория – прямая линия, то движение называется прямолинейным, если кривая – криволинейным.
Способы задания движения.
Задать движение точки по отношению к избранной системе отсчета – это значит указать способ, при помощи которого можно определить положение точки в любой момент времени. Существуют три способа задания движения:
1. Векторный способ
Положение точки в пространстве однозначно определяется заданием радиуса-вектора 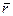 , проведенного из некоторого неподвижного центра 0 в данную точку М.
, проведенного из некоторого неподвижного центра 0 в данную точку М.
Для определения движения точки нужно знать, как изменяется с течением времени 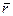 , то есть должна быть известна функция
, то есть должна быть известна функция
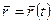 (1)
(1)
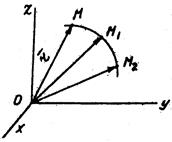
Годографом какого-либо вектора называют кривую, которую вычерчивает конец этого вектора при изменении его аргумента (предполагается, что начало вектора находится в одной и той же точке).
Таким образом, годографом радиуса-вектора является траектория точки.
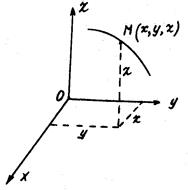
2. Координатный способ
Положение точки М в системе отсчета ОХУ определяется декартовыми координатами 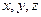 .
.
При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты 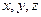 движущейся точки, являются функциями времени.
движущейся точки, являются функциями времени.
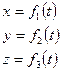 (2)
(2)
Эти уравнения называются уравнениями движения точки в декартовых координатах.
Пусть движение точки М в плоскости задано уравнениями
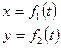
Из первого уравнения выразим время 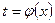 и подставим во второе:
и подставим во второе: 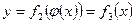 – уравнение траектории точки.
– уравнение траектории точки.
3. Естественный способ задания движения.
Этот способ применяется в том случае, если траектория точки заранее известна. Выберем на траектории неподвижную точку 0, которую назовём началом отсчёта дуговой координаты.
Положение точки М на траектории будем определять дуговой координатой 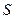 , отложенной на траектории от начала отсчета 0. Расстояния, отложенные в одну сторону от точки 0, будем считать положительными, в другую – отрицательными, то есть установим направление отсчета дуговой координаты.
, отложенной на траектории от начала отсчета 0. Расстояния, отложенные в одну сторону от точки 0, будем считать положительными, в другую – отрицательными, то есть установим направление отсчета дуговой координаты.
При движении точки М расстояние 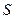 от этой точки до неподвижной точки 0 изменяется с течением времени:
от этой точки до неподвижной точки 0 изменяется с течением времени:
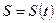 (3)
(3)
– уравнение движения точки М.
Скорость точки
1. При векторном способе задания движения
Пусть в момент времени 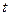 положение точки М определяется
положение точки М определяется 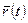 , а в момент
, а в момент 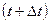 –
– 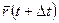 .
.
Вектор 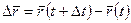 будем называть вектором перемещения точки за время
будем называть вектором перемещения точки за время 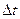 . Отношение
. Отношение 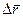 к
к 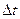 называется средней скоростью за промежуток времени
называется средней скоростью за промежуток времени 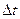 .
. 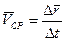 (4)
(4)
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое при стремлении этого промежутка времени к нулю.
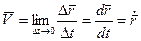 (5)
(5)
Скорость точки – это вектор, направленный по касательной к траектории в сторону движения.
2. При координатном способе задания движения.
Пусть движение точки задано координатным способом
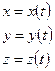
Тогда для радиуса-вектора точки М можно записать
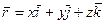 (*)
(*)
где 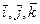 – единичные орты осей
– единичные орты осей 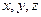 соответственно.
соответственно.
Согласно (5) 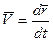 дифференцируем (*)
дифференцируем (*)
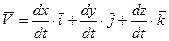 (**)
(**)
Для вектора 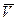 справедливо соотношение:
справедливо соотношение:
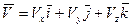 (***)
(***)
где 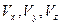 – проекции
– проекции 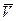 на оси
на оси 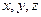 .
.
Сравнивая (**) и (***), получим
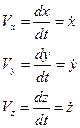 (6)
(6)
Модуль скорости точки
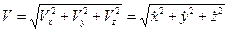 (7)
(7)
Направление скорости определяется направляющими косинусами:
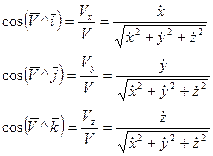
3. При естественном способе задания движения
Пусть в момент времени 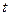 положение точки М определяется координатой
положение точки М определяется координатой 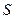 , в момент
, в момент 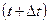 –
– 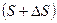 .
.
Согласно (5)
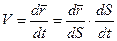 (*)
(*)
Вычислим модуль и определим направление 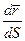 :
:
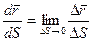
Вектор 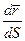 направлен так же, как
направлен так же, как 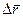 . При
. При 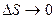 направление этого вектора стремится к направлению касательной к траектории в точке М. Обозначим единичный орт касательной через
направление этого вектора стремится к направлению касательной к траектории в точке М. Обозначим единичный орт касательной через 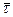 .
.
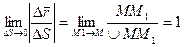
Таким образом 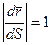 , следовательно
, следовательно 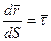 , так как
, так как 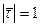 .
.
И равенство (*) принимает вид:
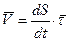 (8)
(8)
Модуль 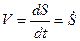 , направление
, направление 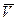 совпадает с
совпадает с 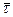 .
.
ЛЕКЦИЯ 6
Ускорение точки.
1. При векторном способе задания движения
Предположим, что в момент времени 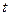 скорость, точки –
скорость, точки – 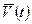 , а в момент
, а в момент 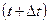 –
– 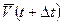 .
.
Предел приращения скорости к приращению времени 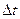 , за которое произошло это приращение, при условии, что
, за которое произошло это приращение, при условии, что 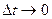 , называется ускорением точки в данный момент времени
, называется ускорением точки в данный момент времени
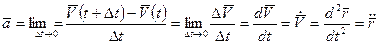 (9)
(9)
Годографом скорости называется кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости проводится из одной и той же точки.
2. При: координатном способе задания движения
Вектор скорости точки
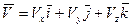
С учетом.(9)
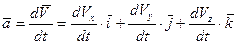 (*)
(*)
На для вектора ускорения точки имеем
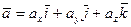 (**)
(**)
Сравнивая (*) и (**), получим
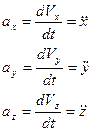
Модуль ускорения точки
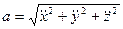
Направление вектора ускорения определяется направляющими косинусами
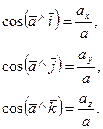
3. При естественном способе задания движения
Пусть известна траектория точки. Возьмем две близкие на траектории точки М и М1 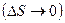 . Проведем касательные к траектории в точках М и М1 –
. Проведем касательные к траектории в точках М и М1 – 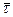 и
и 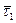 .
.
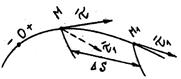
Вектор 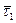 перенесем в точку М параллельно ему самому и проведем плоскость через
перенесем в точку М параллельно ему самому и проведем плоскость через 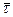 и
и 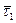 . Эта плоскость называется соприкасающейся плоскостью.
. Эта плоскость называется соприкасающейся плоскостью.
Дата добавления: 2015-02-10; просмотров: 852;
