Построение графиков в декартовой системе координат

Все основные типы графиков и инструменты работы с ними расположены на рабочей панели Graph (График) семейства Math (Математические). На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат.

В MathCAD существует несколько способов построения графиков, однако, первый шаг для всех способов будет один и тот же. Этим первым шагом является введение специальной заготовки для будущего графика – так называемой графической области. Ввести графическую область, как для декартового, так и для любого другого графика можно либо с панели Graph (Графические), либо командой одноименного подменю меню Insert (Вставка).

Графическая область представляет собой две вложенные рамки, как это показано на рис. 5.10, а. Во внутренней области отображаются непосредственно кривые зависимостей. Пространство между рамками служит для визуализации разного рода служебной информации. Графическую область можно увеличивать и уменьшать с помощью специальных маркеров, расположенных на ее внешней рамке. Перемещать по документу и удалять графические области можно точно так же, как простые формулы.

а)

b)

Рис. 5.10. Графическая область в декартовой системе координат

После того как графическая область будет введена, в общем случае требуется задать два соразмерных вектора, определяющих значения координат точек. Сделать это можно различными способами. Наиболее простым и часто используемым методом задания координатной сетки является так называемый быстрый метод. При его применении пользователь задает только имя переменной и вид функции, а шкалы осей и величину шага между узловыми точками автоматически определяет система.

Для построения графика функции по быстрому методу, необходимо выполнить следующую последовательность действий:

1. Введите графическую область.

2. В специальном маркере, расположенном в центре под внутренней рамкой графической области, задайте имя независимой переменной.

3. В центральный маркер, расположенный слева от внутренней рамки, введите функцию или имя функции (если функцию определить раньше переменной, то работа даже упрощается, так как независимая переменная будет задана автоматически).

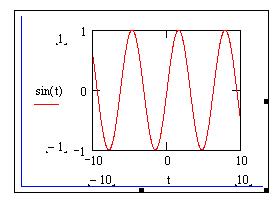
На рис. 5.10, b показан график функции y=sin(t), построенный по быстрому методу.

К недостаткам рассматриваемого метода относится, прежде всего, то, что область изменения переменной для всех функций определяется одна и та же: от –10 до +10. В большинстве же случаев такие пределы будут неприемлемы по целому ряду причин. Например, если амплитуда экстремумов мала по сравнению с изменением величины функции на промежутке, что они становятся просто незаметными.

Чтобы справиться с возникшими трудностями, нужно просто уменьшить интервал изменения либо переменной, либо функции. Для этого выделите графическую область щелчком левой кнопкой мыши. При этом визуализируются все элементы, которые до этого были скрыты (рис. 5.11, а).

a)

b)

Рис. 5.11. Графическая область в декартовой системе координат

Непосредственно под крайними значениями (для оси X) или слева от них (для оси Y) появятся цифры, отражающие максимальные и минимальные величины координат узловых точек графика. Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой.

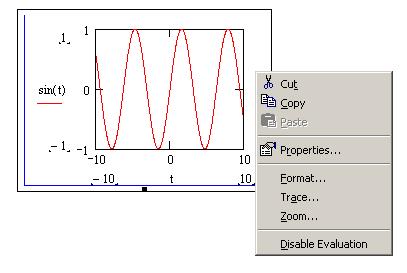
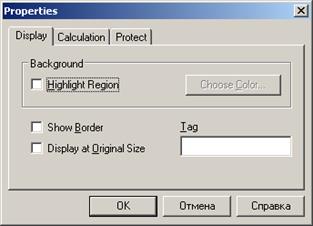
Графическую область можно отформатировать – изменить внешний вид и цветовую гамму. Для этого можно воспользоваться командой Properties (Свойства) из контекстного меню графика (вызывается щелчком правой кнопкой мыши на графической области), как это показано на рис. 5.11, b.

В окне Properties(Свойства) для подавляющего большинства пользователей объективно могут быть полезны два параметра, расположенных на вкладке Display (см. рис. 5.11, b):

a) Highlight Region (Цветная область). Установив этот флажок, вы сможете на палитре Choose Color (Выбор цвета) определить наиболее подходящий цвет заливки для вашей графической области.

b) Show Border (Показать границу). Параметр отвечает за отображение внешней границы графической области. По умолчанию она не визуализируется.

При исследовании функции большое применение находит команда Trace (След) из контекстного меню графика. Эта команда позволяет считать с графика текущее значение аргумента и соответствующего ему значение функции. В результате выполнения этой команды открывается окно «X-Y Trace», как это показано на рис. 5.12. Чтобы активизировать трассировку, нужно мышью щелкнуть по графику. В результате на графике появляются две линии – вертикальная и горизонтальная, которые легко с помощью мыши перемещаются по графической области, а координаты точки пересечения линий отражается в окне трассировки.

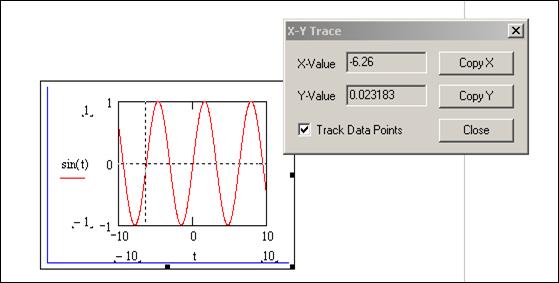
Рис. 5.12. Считывание координат точки на графике

Глава 6
ИСПОЛЬЗОВАНИЕ ПАКЕТА MATHCAD В ЗАДАЧЕ ИССЛЕДОВАНИЯ МАТЕМАТИЧЕСКИХ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Исследование функции является одним из важнейших приложений теории пределов, непрерывности функции и производных. Полная схема исследования функции и построения ее графика объединяет в себе три этапа:

1. Элементарное исследование.

2. Исследование графика функции с помощью первой производной.

3. Исследование графика функции с помощью второй производной.

При этом на каждом из этапов решаются частные задачи, которые позволяют в целом получить свойства функции и оценить ее поведение в различных областях ее определения:

1. Элементарное исследование.

a. Найти область определения функции.

b. Исследовать функцию на симметричность, периодичность, четность и нечетность.

c. Вычислить предельные значения функции в ее граничных точках.

d. Выяснить существование асимптот и получить их уравнения в том случае, если они есть.

e. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.

f. Сделать эскиз графика функции, используя полученные результаты.

2. Исследование графика функции с помощью первой производной:

a. Найти точки, подозрительные на экстремум из решения уравнени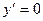й и .

b. Точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия существования экстремума, определить вид экстремума.

c. Вычислить значения функции в точках экстремума.

d. Найти интервалы монотонности функции.

e. Нанести на эскиз графика экстремальные точки.

f. Уточнить вид графика функции согласно полученным результатам.

3. Исследование графика функции с помощью второй производной.

a. Найти точки, «подозрительные» на точки перегиба из решения уравнений: y”(х)=0 и y”(х)=¥.

b. Точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия.

c. Вычислить значения функции в точках перегиба.

d. Найти интервалы выпуклости и вогнутости графика функции.

e. Нанести на эскиз графика точки перегиба.

f. Окончательно построить график функции.

Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.

Очевидно, что проведение полного анализа – очень трудоемкая задача. А решение некоторых вопросов, например, проверка функции на периодичность, требует знаний из областей математики, не входящих в учебную программу. Тем не менее, пакет MathCAD может оказать большую помощь при исследовании функций, особенно в тех случаях, где требуется решение уравнений и неравенств. А технология построения графиков функций, используемая системой MathCAD, позволяет проверять найденные решения практически на любом из этапов исследования.