Определение и использование пользовательских функций

Важным инструментом в математических вычислениях являются пользовательскиефункции. Функции особенно целесообразно использовать, когда приходится производить многократные вычисления по одним и тем же формулам, но с разными исходными данными.

Чтобы воспользоваться собственной функцией, нужно:

· Описать функцию.

· Вызвать описанную функцию для выполнения.

Очевидно, что описание/определение функции должно быть расположено выше, чем ее использование. Для определения функции используются идентификаторы: имя функции и имена формальных параметров функции. Формальный параметр – это идентификатор, конкретное значение которого определяется путем замены его на соответствующее ему значение фактического параметра при обращениик функции. Функции однозначно ставят в соответствие значениям аргументов (формальным параметрам) значения фактических параметров функции.

Формат определения функции:

Имя_функции(список формальных параметров) := выражение

Вызов пользовательской функции производится подобно тому, как и в случае вызова любой стандартной функции.

Можно поместить результат в отдельную переменную:

Имя_переменной_результата:=Имя_функции(список_фактических параметров)

Или напечатать:

Имя_функции(список_фактических параметров)=

Пример 1. Требуется определить функцию Dist, которая будет возвращать расстояние заданной точки от начала координат. Использовать эту функцию для вычисления расстояний от точек А(1.96; –3.8) и
В(6; 42.5) до начала координат.

Решение. Из курса линейной алгебры известно, что расстояние от начала координат до некоторой точки A(x, y) определяется по формуле 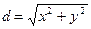. Здесь (x, y) – координаты заданной точки. Эта формула и будет составлять основу функцию Dist. При описании функции следует предусмотреть два формальных параметра — координаты точки. На место этих параметров должны будут вписаны фактические координаты заданных точек.

В соответствии с формулой определения расстояния от точки на плоскости до начала координат функция Dist может быть записана в виде: 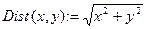. А обращение к функции Dist для вычислений расстояний от заданных точек может быть представлено в виде:

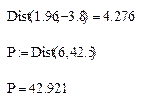
Во втором случае результат помещается во вспомогательную переменную.

Пример 2. Дана функция вида: 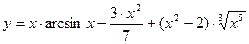. Требуется найти ее максимальное и минимальные значения.

Решение. Для решения поставленной задачи целесообразно воспользоваться функцией поиска максимального значения
maximize(f, var1, var2, ...),которая имеется в библиотеке стандартных функций системы MathCAD. Первым параметром у этой функции должно быть имя пользовательской функции, максимальные значения которой требуется найти. Следующие параметры задают имена переменных, в которых будут помещены искомые значения. В нашем случае это будет одна переменная х. Чтобы воспользоваться этой функцией, необходимо поставить перед ней блок решения с ключевым словом Given (Дано). Кроме этого итерационный алгоритм, обеспечивающий решение поставленной перед функцией maximize задачи, требует задания начальных значений искомого аргумента. Установку начальных значений следует произвести до блока решения. Аналогичное описание у функции minimize которая предназначена для поиска минимального значения определенной функции. Фрагмент с решением задачи представлен на рис. 5.7.

Рис. 5.7. Поиск максимального и минимального значений заданной функции