Решение неравенств

Для аналитического решения неравенств в MathCAD используется тот же самый оператор solve, расположенный на панели Symbolic (Символьные), что и для решения уравнений.

Пример 5. Требуется решить неравенство вида: 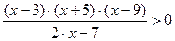в символьном виде.

Решение. Процесс решения задачи можно свести к выполнению следующих шагов:

1. Выполнить команду solve, расположенную на панели Symbolics (Символьные).

2. Заполнить предоставленный шаблон.

3. Проанализировать результат.

4. Решение неравенства из примера 5 предоставлено системой в виде, как это показано на рис. 6.10.

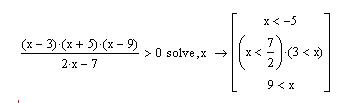
Рис. 6.10. Решение неравенства

Полученное решение соответствует следующей записи в стандартной форме: .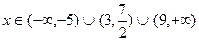

Как вы уже, наверное, заметили, MathCAD выдает ответы в несколько отличном, от принятом в нашей математике, виде. Поэтому зачастую самой трудной частью работы при символьном решении неравенств является интерпретация результата. Тут нужно запомнить несколько правил:

Ответ оператор solve возвращает в виде вектора, содержащего элементарные неравенства. Каждое такое неравенство описывает область, в которой решаемое неравенство справедливо.

Если область открытая (то есть одной из ее границ является бесконечность), то задающее ее элементарное неравенство будет иметь вид х>а или х<а. В стандартном виде такие области запишутся как 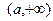или .

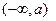Если область замкнута и ее границам соответствуют значения аргумента а и b, то она будет описана элементарным неравенством вида 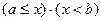. В стандартном виде эта запись будет выглядеть как .

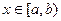Области в векторе ответа будут расположены строго в направлении числовой оси. Поэтому преобразовывать в стандартную форму его можно чисто механически, сохраняя исходный порядок областей. Для объединения обозначений областей в одно выражение используется символ « ».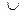

Пример 6. Требуется найти область определения функции .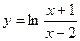

Решение. Как известно, под областью определения функции понимают совокупность значений аргумента, при которых выражение, определяющее функцию, имеет смысл. Область определения заданной функции определяется из следующих условий:

аргумент логарифма может принимать только положительные значения;

знаменатель у дроби, стоящей под знаком логарифма не должен обращаться в нуль (х¹2);

числитель не должен обращаться в нуль (х¹1).

На начальном этапе можно решить неравенство 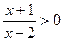. А затем из полученной области исключить точки –1 и 2. Решение неравенства: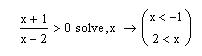

Что соответствует области: 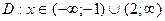. В исключении точек
–1 и 2 нет необходимости, так как они не входят в означенную область.

Пример 7. Требуется найти область определения функции 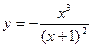. Если имеются точки разрыва, то установить тип разрыва.

Решение. Поскольку аналитическое выражение функции представлено в виде дроби, а знаменатель дроби не может быть равен 0, из области определения функции следует исключить точку 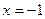, т.е. 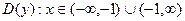. Т.е. точка 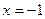является точкой разрыва. Чтобы найти тип разрыва следует найти односторонние пределы (команды следует взять с панели Calculus (Вычислить)):

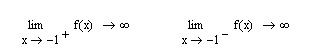
Вывод. Так как односторонние пределы равны ¥, то имеет место неустранимый разрыв 2-го рода, а точка 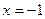является точкой бесконечного скачка функции.

Пример 8. Требуется найти все асимптоты графиков функции 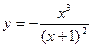. Найти подтверждение правильности решения на графике функции.

Решение. Известно, если точка 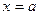является точкой бесконечного разрыва функции, то прямая 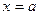есть вертикальная асимптота графика функции. В предыдущем примере было установлено, что точка 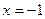является такой точкой бесконечного разрыва. Следовательно, прямая 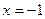является вертикальной асимптотой графика заданной функции. Для получения наклонных асимптот нужно вычислить пределы: 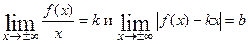. Если эти пределы существуют, то прямая 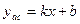есть наклонная асимптота графика функции. Вычисление пределов и уравнение наклонной асимптоты представлены на
рис. 6.11.

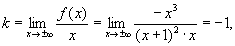
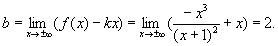
Рис. 6.11. Вычисление параметров наклонной асимптоты

Таким образом, уравнение наклонной асимптоты имеет вид: 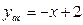. Анализ построенного графика функции и ее асимптот, представленного на рис. 6.12, показывает, что расстояния текущей точки кривой 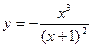до каждой из асимптот стремится к нулю по мере удалении этой точки по кривой в бесконечность, что соответствует определению асимптоты.

Следует обратить внимание на формулу в определении вертикальной асимптоты, представленной на рис. 6.12. Здесь значение функции равно х, а область аргумента соответствует постоянному значению –1.

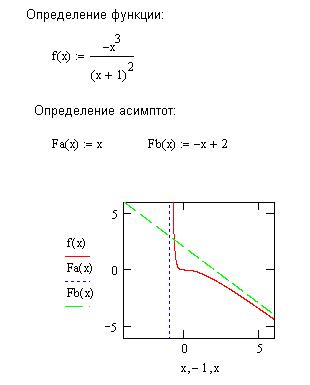
Рис. 6.12. Графическая интерпретация связи графика с асимптотами

Пример 9. Требуется на графике функции 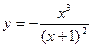найти точки, подозрительные на экстремум (критические точки).

Решение. Воспользуемся необходимым условием существования экстремума: если функция непрерывна в точке х₀ и ее окрестности и принимает в этой точке экстремальное значение, то первая производная f’(х₀) либо равна нулю или бесконечности, либо не существует. Следовательно, для того, чтобы найти точки, подозрительные на экстремум, следует найти решение уравнени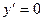й: и 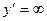. Решение представлено на рис. 6.13.

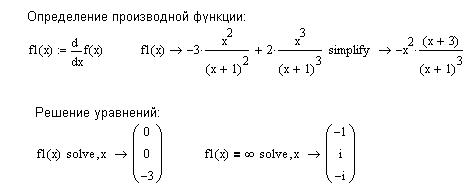
Рис. 6.13. Определение критических точек графика функции

Из предоставленных решений берем только действительные корни:

.

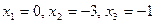Пример 10. Требуется на графике функции 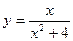найти точки, подозрительные на точки перегиба. Найти подтверждение правильности решения на графике функции.

Решение. Необходимое условие точки перегиба: если х₀ – точка перегиба кривой y=f(х), то вторая производная f’’(х₀) либо равна нулю или бесконечности, либо не существует. Решение представлено на
рис. 6.14. На рис. 6.15 изображены функция и ее вторая производная.

Рис. 6.14. Определение точек перегиба графика функции

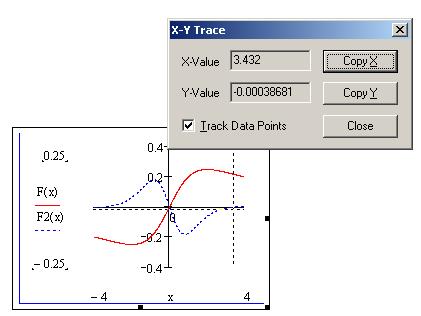
Рис. 6.15. Графика функции F(x) и ее второй производной F2(x)

Пример 11. Требуется найти максимум функции 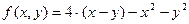при ограничениях, заданных неравенствами вида: .

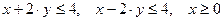Решение. Для решения поставленной задачи можно воспользоваться следующей схемой [20]:

Определить функцию.

Задать начальные условия.

Инициировать блок решения, в котором:

3.1. Задать ограничения.

3.2. Вычислить максимальное значение функции с помощью стандартной функции maximize, описанной в примере 2 главы 5.

Отобразить результат вычислений.

Решение представлено на рис. 6.16.

Рис. 6.16. Решение неравенства