Нахлесточные соединения с фланговыми швами

В случае действия статической нагрузки на растяжение, сжатие или срез (рис.10.4) угловые швы рассчитываются на прочность по формуле

(10.2)

или 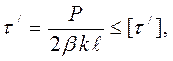(10.3)

где Р – величина силы, кН;

k- катет шва, мм;

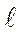– длина шва.

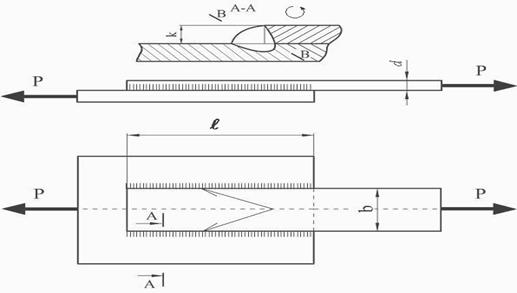
Рисунок 10.4 - Схема нагружения фланговых швов

Исходя из условия прочности можно определить максимальное напряжение:

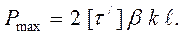(10.4)

Соответственно приведенным выражениям распределение напряже-ний по длине шва равномерно. Фактически напряжения распределены не-равномерно. Эпюра напряжений имеет вид, показанный на рисунке 10.5. Наиболее нагруженные участки расположены в начале и конце шва. Кон-центрацию напряжений по длине шва можно определить:

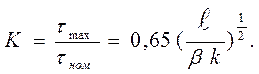(10.5 )

Из выражения следует, что значение коэффициента концентрации пропорционально длине шва. Поэтому длину шва можно ограничить, при-нимая не большей, чем (10.6)

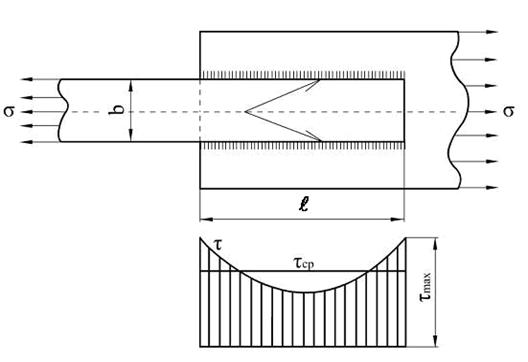
Рисунок 10.5 - Схема распределения напряжений в шве

В случае, когда изгибающий момент воспринимается фланговыми швами, расчет выполняют исходя из условия

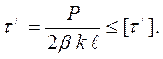
В этом случае изгибающий момент М уравновешивается реактив-ным моментом М_р = М (рис.10.6). При этом реактивный момент рассмат-ривают как пару сил N, умноженную на величину плеча H:

(10.7)

В свою очередь,

Принимая силу N как осевую, условие прочности можно записать:

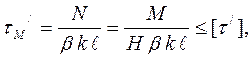(10.8)

где – плечо реактивной пары.

Рисунок 10.6 - Схема нагрузки фланговых швов изгибающим моментом

Если такое соединение нагрузить изгибающим моментом и растяги-вающей нагрузкой (рис.10.7), тогда

(10.9)

Рисунок 10.7 - Схема действия двух сил на сварное соединение

Напряжения от Р и М определяются отдельно, как и в предыдущих случаях. Поскольку направления напряжений совпадают, то

(10.10)

В нахлесточных соединениях относительно большой ширины напря-жения на участке между фланговыми швами будут неравномерными (рис.10.8).

Рисунок 10.8 - Схема концентрации напряжений в основном металле

Коэффициент концентрации напряжений в этом случае

(10.11)

где a, – геометрические размеры накладки.

Наличие концентрации напряжений определяет характер разрушения фланговых швов. Траектория разрушения фланговых швов показана на рис.10.9.

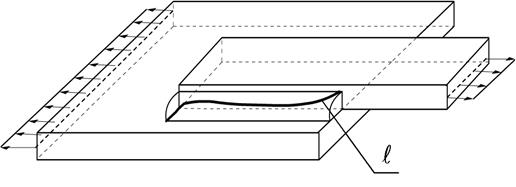
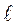- линия разрушения шва

Рисунок 10.9 - Траектория разрушения шва

В средней части шва разрушение происходит по меньшему сечению, в крайних участках шва выходит на катет, через который проходят сило-вые потоки.

10.3 Нахлесточные сварные соединения с лобовыми швами

Лобовые швы нахлесточных сварных соединений можно проверить по выражению

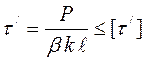
в случае, если соединение является односторонним (рис.10.10).

Рисунок 10.10 - Соединение с односторонней накладкой

Максимальная нагрузка для такого соединения

Р_max = [τ^/ ]β k 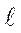. (10.12)

Если имеет место соединение, выполненное по схеме, показанной на рисунке 10.11, условие прочности имеет вид

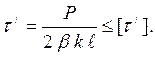(10.13)

Расчет прочности ведут относительно опасного сечения основного металла(А-А) и бессектрисы углового шва (В-В).

Рисунок 10.11 - Двустороннее соединение с лобовыми швами

При проектировании таких швов необходимо обеспечить расстояние между швами (С) больше, чем четыре толщины d, т.е. 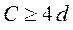. При невыполнении такого условия происходит деформация сварного соединения, как показано на рисунке 10.12.

Рисунок 10.12 - Деформация сварного соединения

В случае, когда лобовым швом воспринимается изгибающий момент (рис.10.13), величину напряжений можно определить:

(10.14)

где W – момент сопротивления сварного шва.

Учитывая, что (10.15)

величина напряжений будет равна: (10.16)

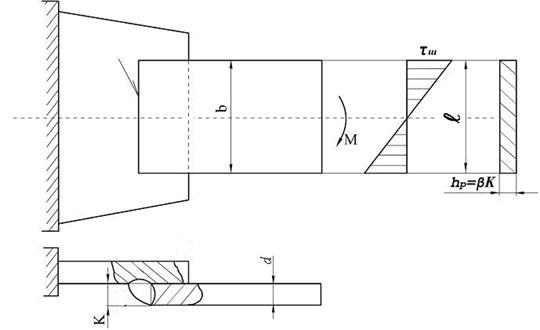
Рисунок 10.13 - Схема нагрузки лобового шва

Когда в сварном шве на некотором расстоянии а действует попереч-ная сила Р (рис.10.14), в нем возникают напряжения среза от силы Р, τ^м_ш - от действия момента, вызванного этой силой:

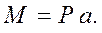(10.17)

Результирующие касательные напряжения рассчитывают по формуле 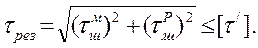(10.18)

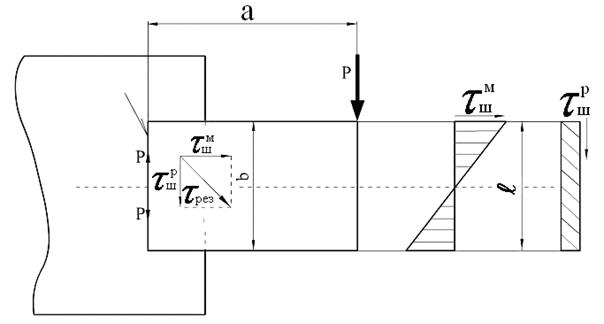
Рисунок 10.14 - Схема нагрузки лобового шва

Рассмотрим расчет угловых сварных швов, которые прикрепляют уголки(рис.10.15).

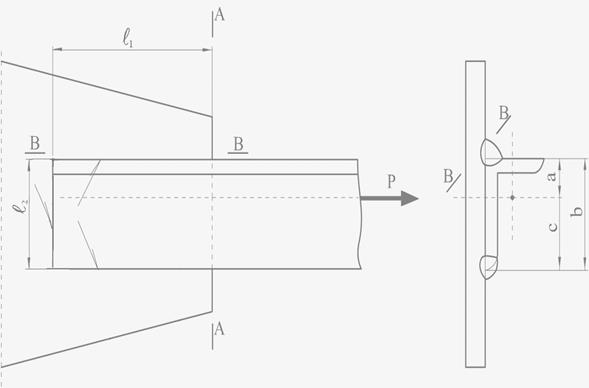
Рисунок 10.15 - Соединение с уголком

Особенность расчета заключается в том, что величина силы Р между швами распределяется обратно расстоянию от шва до центра массы уголка.

Приложенная сила Р распределяется таким образом:

Р = Р_л + Р_ф, (10.19)

где Р_л – часть силы Р, что воспринимается лобовым швом,

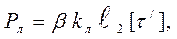(10.20)

где - коэффициент, который учитывает способ сварки;

k_л – катет лобового шва, максимальное значение которого назначают в зависимости от толщины полки уголка (S = 2мм);

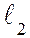– длина лобового шва, которая равняется ширине полки уголка;

Р_ф – сила, которая воспринимается фланговыми швами, то есть

Р_ф = Р_Т + Р_Н, (10.21)

где Р_т, Р_н – силы, которые воспринимают тавровое и нахлесточное соединения соответственно.

Распределение усилия между этими соединениями можно учесть ко-эффициентом С_т или С_н . Величины коэффициентов приведены в таблице 10.1

Таблица 10.1 - Коэффициенты распределения усилия

Элемент, который приваривается	Эскиз соединения	Коэффициент
Ст	Сн
Неравнополочный, приваренный меньшей полкой уголок		0,75	0,25
Неравнополочный, приваренный большей полкой уголок		0,65	0,35
Равнополочный уголок		0,7	0,3

Условия прочности для фланговых швов будут иметь вид:

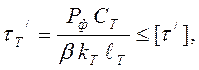(10.22)

(10.23)

Исходя из приведенных условий можно рассчитать длины швов.