Работа деформации

Кроме уже названных характеристик механических свойств материа-ла диаграмма растяжения позволяет определить еще и энергетические его характеристики.

Площадь диаграммы растяжения в координатах Р-D 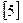характери-зует работу, израсходованную на разрыв образца. Пусть некоторой растягивающей силе Р отвечает деформация λ образца (рис. 2.5). При бесконечно маленьком приросте dА прирост деформации будет dλ. Работа внешних сил на этом перемещении

dA = (P + dP)dλ = Pdλ.

Рисунок 2.5 Рисунок 2.6

Работа, которая израсходована при растяжении образца на удлине-ние λ₁, будет равна:

А =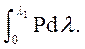

Из рисунка 2.5 видно, что работа, израсходованная на разрыв образ-ца, будет равняться всей площади OABCDEFGO диаграммы растяжения. В пределах упругости полная работа деформации определяется площадью треугольника (рис.2.6, а):

А_пр = 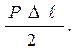(2.17)

Удельная работа деформации а_пр , то есть работа, которая израсходо-вана на деформацию единицы объема материала, определяется по формуле

а_пр = А/ V ,

где V = F_{0 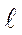0},

тогда а _пр = 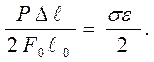(2.18)

Удельная работа деформации в пределх упругости определяется пло-щадью треугольника на диаграмме σ - 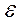(см. рис.2.6,б) и характеризует способность материала оказывать сопротивление ударному действию наг -рузки: чем большая удельная работа деформации до разрыва, тем лучше материал оказывает сопротивление ударным нагрузкам.