Разгрузка и повторная нагрузка
Если при растягивающей силе, вызывающей напряжение, не превы-шающее предел упругости, прекратить нагрузку и разгрузить образец, то его удлинение полностью исчезнет. Будет иначе, если к началу нагруже-ния напряжение в образце превысит предел упругости.
Точка М. Выполнив разгрузку, заметим, что этот процесс на диаг-рамме описывается уже не по кривой, совпадающей с кривой нагрузки ОАВСДМ (см.рис.2.1, в), а по прямой МN, параллельной прямолинейно-му участку ОА диаграммы. Предыдущее растяжение за пределом текучес-ти повышает предел пропорциональности и уменьшает остаточное удлине- ние образца после разрыва, делая его более коротким. Удлинение D  при разгрузке полностью не исчезает, так как
при разгрузке полностью не исчезает, так как
D 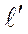 = D
= D 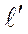 упр + D
упр + D 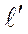 0,
0,
где D 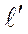 0, - оставшаяся часть удлинения образца за пределом упру-гости.
0, - оставшаяся часть удлинения образца за пределом упру-гости.
Если вновь начать нагружать образец, который был растянут силой, вызвавшей в нем напряжение выше σТ, а затем разгрузить, то окажется, что линия повторного нагружения почти совпадает с линией разгрузки MN. Предел пропорциональности σпц повысится и станет приблизительно равным тому напряжению, до которого первоначально был растянут обра-зец. При дальнейшем увеличении Р кривая диаграммы совпадет с MEF. Часть диаграммы, расположенная по левую сторону от линии MN, ока -жется отсеченной, то есть начало координат переместится в точку N. Ос-таточное удлинение после разрыва образца будет меньше, чем в образце, не подвергавшемся предыдущей пластической деформации. Таким образом, предварительная вытяжка образца за пределом текучести повышает σпц, уменьшает остаточное удлинение после разрыва и делает образец более хрупким. Это изменение свойств материала за пределом текучести называется наклёпом.
Полное удлинение образца за пределом упругости состоит из двух частей – упругой (D 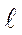 упр) и пластической (D
упр) и пластической (D 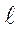 0):
0):
D 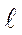 = D
= D 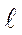 упр + D
упр + D 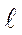 0.
0.
После разрыва образца, когда упругая составляющая полного удли-нения в его обеих частях исчезает (отрезок D 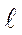 упр), отрезок D
упр), отрезок D 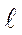 0 соответ-ствует оставшемуся удлинению.
0 соответ-ствует оставшемуся удлинению.
Диаграмма растяжения в координатахσ - 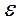
Вид диаграммы растяжения в координатах Р - 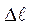
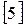 зависит не то-лько от свойств материала, но и от размера испытываемого образца. Диаграмма, которая характеризует только механические свойства материала, получается перестройкой первичной диаграммы растяжения в координатах σ -
зависит не то-лько от свойств материала, но и от размера испытываемого образца. Диаграмма, которая характеризует только механические свойства материала, получается перестройкой первичной диаграммы растяжения в координатах σ - 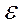 (рис.2.2, а), где σ = P/F0, а ε =
(рис.2.2, а), где σ = P/F0, а ε = 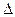
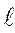 /
/ 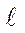 0, в диаграмму с координатами σ – ψ(рис.2.2, б).
0, в диаграмму с координатами σ – ψ(рис.2.2, б).
Точки о, а, в, с, d, e, f отвечают точкам О, А, В, С, Д, Е, F диаграм-мы Р-D 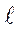 (см. рис.2.1). Из диаграммы σ –
(см. рис.2.1). Из диаграммы σ – 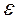 видно, что tgα = σ /
видно, что tgα = σ / 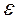 = Е, то есть модуль упругости при растяжении равняется тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс. После образования шейки относительная продольная деформация распределяется по длине образца не равномерно, и действительная диаграмма растяжения строится в координатах: относительное сужение поперечного сечения в шейке
= Е, то есть модуль упругости при растяжении равняется тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс. После образования шейки относительная продольная деформация распределяется по длине образца не равномерно, и действительная диаграмма растяжения строится в координатах: относительное сужение поперечного сечения в шейке 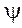 и отвечающее ему действительное напряжение σ, где
и отвечающее ему действительное напряжение σ, где  = (F0 – Fк) / F0;
= (F0 – Fк) / F0;
σ = Рі /Fі , а Рі и Fі – соответственно усилие и наименьшая площадь поперечного сечения образца в момент испытания (см.рис.2.2, б).
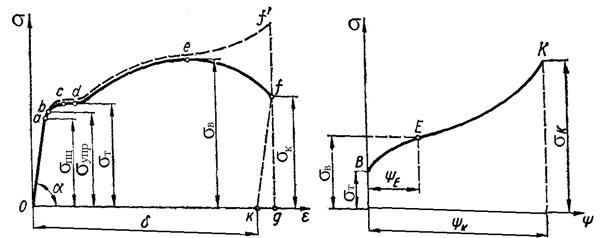
Кривая, отвечающая действительным напряжениям при растяжении изображена на рис.2.2,б. Точка В отвечает началу возникновения остаточ-ной деформации и действительному напряжению – пределу текучести. Точка Е отвечает максимальной силе Рmax, которую выдерживает образец во время испытания. По ней определяется действительное временное соп -
ротивление (предел прочности). Абсцисса точки К представляет наиболь-шее сужение сечения образца ψк, а ордината – соответствующее ему дейс-твительное напряжение в момент разрыва σ к. Из этой диаграммы видно, что сопротивление пластическому деформированию возрастает вплоть до наступления разрушения.
А б
а – вид диаграммы в координатах σ - 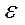 ;
;
б – вид кривой, отвечающей действительным напряжениям при растяжении низкоуглеродистой стали
Рисунок 2.2 – Вид диаграммы растяжения низкоуглеродистой стали в координатах: σ – 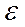 ,S – ψ
,S – ψ
Дата добавления: 2015-01-10; просмотров: 1539;
