Электронно-конформационные взаимодействия
Концепция ЭКВ исходит из того, что изменение зарядового или электронного состояния системы приводит к изменению конформации, что в свою очередь индуцирует изменение электронного состояния. Амплитуды конформационных движений относительно велики. Для их описания непригодна модель гармонических колебаний, применяемая в теории электронно-колебательных взаимодействий. Нужно иметь дело с уравнением Ланжевена для осциллятора в системе с трением:
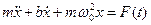
m — эффективная масса сегмента, b — коэффициент трения, ω0 круговая частота осциллятора, F(t) — случайная сила, действующая на осциллятор со стороны окружающих частиц. F(t) обусловлена тепловыми флуктуациями среды. Частоты этих конформационных движений значительно меньше частот амидных групп (ν < 200 см -1 для крутильных колебаний вокруг C – N - связи).
Предполагают, что конформационное движение представляет собой ограниченную непрерывную диффузию в протяжённой потенциальной яме малой глубины. Такое движение описывается уравнением Фоккера-Планка:
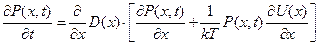 .
.
P(x, t) — плотность вероятности найти систему в момент t в конформации со значением координаты x; D(x, t) — коэффициент конформационной диффузии, U(x) — конформационный потенциал;
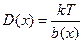 .
.
b(x) — коэффициент трения.
Температурная зависимость давления определяется зависимостью D(x) от энергии активации е(x):
D(x) = D0 exp (- е(x)/kT).
Сравнительно крупные конформационные движения в белковой глобуле возможны вследствие наличия или возникновения в ней свободных, “пустых” участков — дырок.
Таким образом, с точки зрения динамики белковая глобула — сложная структурированная система, обладающая целым набором конформационных движений с различными временами.
Перемещение любого лиганда, начиная с электрона, в макромолекуле вызывает изменение электронной плотности и, вслед за ним, конформационого состояния системы. Система “электронная плотность лиганда + конформационная деформация фермента (или макромолекулы)” подобна полярону в физике твёрдого тела и называется конформоном. (Волькенштейн).
Конформон отличается от полярона сильной нелинейностью. Конформон не может перемещаться на большие расстояния без диссипации энергии. Быстрая диссипация определяется неоднородностью, апериодичностью глобулы. Для реализации ферментативного процесса достаточно коонформационной перестройки в пределах нескольких связей.
Движение к активному центру — это движение конформона. Оно происходит путём конформационного раскрытия некоторой щели в глобуле, характеризуемой определённой микровязкостью. Структурное соответствие E-S имеет динамический характер; количественной мерой соответствия может служить критическая энергия деформации щели, соответствующей размеру и форме молекулы субстрата. Движение конформона описывается уравнением Фокккера-Планка.
Экспериментально было показано, что электронные изменения в АЦ фермента сильно влияют на конформационные свойства белка как целого. При этом в ферментативной системе происходит выравнивание энергетических уровней различных промежуточных форм и понижение активационных барьеров. В этом и проявляется комплементарность профилей химической (электронной) и конформационной свободных энергий. Комплементарность определяется ЭКВ.
Теоретические подходы к ЭКВ развиты Догонадзе (и сотрудниками), и Шайтаном. Движения атомных ядер в белках характеризуются амплитудами и временами, представленными в таблице №1:
Табл. №1. Характерные амплитуды и времена тепловых флуктуаций элементов структуры белка при Т=300 К.
| Процесс | Амплитуда, нм | Время, с |
| Валентные колебания | 0,001 – 0,01 | 10 -12 |
| Микроконформационные движения боковых групп | 0,03 – 0,1 | 10 -8 – 10 -9 |
| Изгибные движения (от α или β участков цепи) | 0,2 – 0,7 | 10 -5 – 10 -7 |
При попадании электрона в поляризуемую среду, образованную группами макромолекулы, происходят ЭКВ. Среда поляризуется и образуется самосогласованное поле, эквивалентное потенциальной яме для электрона. Такое образование в физике твёрдого тела называют поляроном. Если поляризационная деформация приводит к состоянию, отделённому от исходного энергетическим барьером, то имеем дело с нелинейным поляроном. В биополимерах поляризация приводит к движению по конформационым степеням свободы — нелинейный полярон является конформоном. Чернавский и Чернавская дают грубую оценку энергии и размеров конформона. В среде, содержащей равномерно распределённые ионы массы М, взаимодействующие по закону Кулона, согласно теореме вириала имеем:
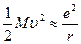 .
.
Скорости v и расстоянию r соответствует частота колебаний ионов:
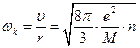 ,
,
где 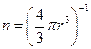 — число ионов в единице объёма.
— число ионов в единице объёма.
Взаимодействуя с колебаниями ионов, электрон приобретает энергию 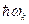 и импульс:
и импульс:
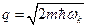 ,
,
где m — масса электрона. Согласно соотношению неопределённостей, соответствующий размер электронного облака равен
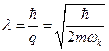 .
.
Размеры нелинейного полярона (конформона) должны быть такого же порядка. Энергия поляризации по порядку величины равна 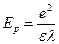 , где е — микроскопическая диэлектрическая проницаемость. Наконец, отношение Ер к энергии колебаний даёт число квантов, участвующих в образовании полярона:
, где е — микроскопическая диэлектрическая проницаемость. Наконец, отношение Ер к энергии колебаний даёт число квантов, участвующих в образовании полярона:
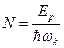
Для белков среднее значение плотности зарядов n~1021 см -3, т.е. расстояние между зарядами ~10Å. Если заряды расположить на протонах, то М ≈ (6,02∙1023)-1 г. Величину ε можно считать равной 3. Получаем ωk ≈ 1013 с-1, размеры полярона λ ≈ 15Å, т.е. поляризацией охвачена практически вся макромолекула. Энергия поляризации ≈ 0,35eV. Сдвиг уровней электрона того же порядка. Наконец, N ≈ 15.
В кинетике ЭКВ можно выделить 4 процесса:
1. Колебания электрона внутри одной потенциальной ямы размером в несколько Å, с частотами ~1017 с-1.
2. Колебания атомов с частотами ~ kТ/h~1013 c-1 и с амплитудами ~ 10-1 – 10-2Å; частоты упругих колебаний белковой глобулы как целого ~ 1011 – 1012 с-1.
3. Туннелирование электрона с характерными временами 10-6 – 10-7 с и расстояниями 10-20 Å.
4. Конформационные переходы в молекуле со временами 10-3 – 10-1 с; возможны и значительно более медленные процессы.
Однако до сих пор нет строгой теории, количественно описывающей скорость ферментативной реакции.
При рассмотрении пути реакции следует учитывать “конформационную” природу явления. Иными словами, положения электронных уровней энергии зависят от динамического состояния среды — белка, обладающего конформационными степенями свободы. Вследствие малой скорости коонформационных движений система является адиабатической.
5. Элементарный акт ферментативной реакции в работах Блюменфельда и Чернавского.
Формулируется постулат, согласно которому конформационное изменение ФСК, следующее за присоединением S к активному центру Е, включает в себя кроме разрыва старых и образования новых вторичных связей в макромолекуле белка также химические изменения S, превращающие S в Р. Т.о., элементарный акт ферментативной реакции заключается в конформационном изменении макромолекулы (ФСК), и скорость превращения S в Р определяется скоростью этого конформационнного изменения.

Рис.13. Схема энергетических изменений на разных стадиях каталитического разрыва связи А-В субстрата: 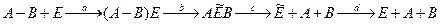
В быстрой стадии (а) присоединения S к E происходит с выделением энергии ∆G1. Конформация белка не успевает измениться и остаётся напряжённой. На стадии (b) происходит медленная релаксация комплекса к новому равновесию и превращение S в P ( 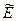 — новая конформация фермента). Свободная энергия понижается на величину ∆G2. Далее, в стадии (c) комплекс распадается на фермент и продукт, но фермент остаётся в напряжённой конформации
— новая конформация фермента). Свободная энергия понижается на величину ∆G2. Далее, в стадии (c) комплекс распадается на фермент и продукт, но фермент остаётся в напряжённой конформации 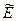 , медленно релаксирующей к стадии (d).Общее понижение свободной энергии ∆G=∆G1+∆G2+∆G3+∆G4. Это — термодинамическая модель, в рамках которой кинетика процесса не рассматривалась. Блюменфельд считает уравнение Аррениуса или Эйринга неприменимым к ферментативным реакциям, утверждая, что система не характеризуется энергией активации в обычном смысле слова. Блюменфельд настаивает на том, что все молекулы субстрата, образовавшие ФСК с Е, релаксирующим к новому конформационному состоянию, претерпевают химическое превращение. Влияние Т на скорость реакции определяется не изменением числа молекул, способных преодолеть активационный барьер, а изменением исходной конформации и, следовательно, изменением пути и скорости последующей релаксации.
, медленно релаксирующей к стадии (d).Общее понижение свободной энергии ∆G=∆G1+∆G2+∆G3+∆G4. Это — термодинамическая модель, в рамках которой кинетика процесса не рассматривалась. Блюменфельд считает уравнение Аррениуса или Эйринга неприменимым к ферментативным реакциям, утверждая, что система не характеризуется энергией активации в обычном смысле слова. Блюменфельд настаивает на том, что все молекулы субстрата, образовавшие ФСК с Е, релаксирующим к новому конформационному состоянию, претерпевают химическое превращение. Влияние Т на скорость реакции определяется не изменением числа молекул, способных преодолеть активационный барьер, а изменением исходной конформации и, следовательно, изменением пути и скорости последующей релаксации.
6.Для построения кинетической теории необходимо исследовать относительную роль двух механизмов переноса электрона: 1) надбарьерный переход по Эйрингу; 2) туннельный эффект. Туннельный эффект при переносе электрона в биологической системе был впервые рассмотрен Чансом.
Константа скорости активационного перехода равна:
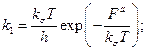
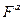 — свободная энергия активации.
— свободная энергия активации.
Число актов перехода в единицу времени равно:
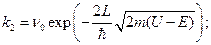
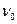 — частота колебаний электрона в молекуле, участвующей в цепи переноса (для цитохрома с —
— частота колебаний электрона в молекуле, участвующей в цепи переноса (для цитохрома с — 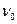 ~ 1017 c-1), L — ширина барьера, U — его высота, Е— уровень энергии электрона, m — масса электрона. Член
~ 1017 c-1), L — ширина барьера, U — его высота, Е— уровень энергии электрона, m — масса электрона. Член 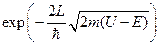 определяет прозрачность барьера.
определяет прозрачность барьера.
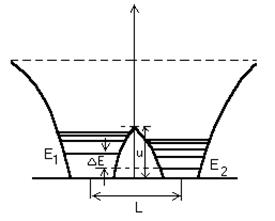
Рис.14. Схема потенциальных ям двух соседних переносчиков: две потенциальные ямы, разделённые барьером.
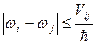 — условие резонанса.
— условие резонанса. 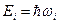 — энергия i-го уровня.
— энергия i-го уровня.
Полная скорость переноса определяется суммой k1+k2. при высоких Т преобладает k1, а при низких Т — k2. Можно предположить, что Fа и U совпадают. Молекулярная система ЦПЭ (цепи переноса электрона) содержит "проводящие группы", в которых р-электроны делокализованы (ароматические группы белков, простетические группы, коферменты, к ним относят и атомы переходных металлов). Размеры таких групп ~ нескольких Å. Проводящие группы отделены друг от друга диэлектрическими молекулами белков и липидов; соответствующие значения ширины барьера L ~ размеров этих молекул. Согласно имеющимся оценкам L ~ 10-20Å, U ~ 1-2 eV. При этих значениях k2>> k1. Отсюда следует, что реальные процессы должны быть практически независимыми от Т, но это противоречит опыту. Контрвозражение: туннельный переход электрона должен сопровождаться излучением фононов, возбуждением колебаний молекул, конформационными переходами, что приводит к сильной температурной зависимости.
Поведение электрона при его туннелировании зависит от соотношения между разностью электронных уровней ∆Е и величиной резонансного расщепления ∆Еr (учитывающего влияние среды, движение ядер, электронно-колебательные взаимодействия).
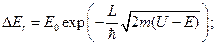
Таким образом, туннельный эффект связан с условиями резонанса электронных уровней энергии.
Если ∆Е >> ∆Еr, то туннельного перехода не будет. При ∆Е≤∆Еr переход произойдёт за время 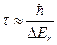 . При L≈ 20Å, (U-E) ≈ 2eV, ∆Еr ≈ 10-6 eV. Реальные значения в ЦПЭ должны быть много больше, и такой идеальный переход невозможен. Туннелирование становится возможным вследствие диссипации энергии, обеспечивающей сближение электронных уровней. Именно ЭКВ создают возможность такой диссипации.
. При L≈ 20Å, (U-E) ≈ 2eV, ∆Еr ≈ 10-6 eV. Реальные значения в ЦПЭ должны быть много больше, и такой идеальный переход невозможен. Туннелирование становится возможным вследствие диссипации энергии, обеспечивающей сближение электронных уровней. Именно ЭКВ создают возможность такой диссипации.
В квантовой механике движение электрона описывается волновой функцией Ψ(x,t), которая при х = х0, попадая на барьер U0, частично отражается, а частично проходит сквозь барьер. Стационарные уравнения Шрёдингера в области 1 и 2 имеют вид:
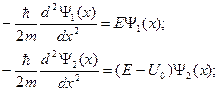
Стационарные состояния с энергией Е описываются волновыми векторами k1 и k2:
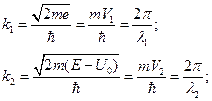
Тогда 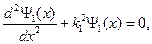
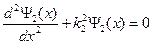 . Вероятность найти частицу в области 2 при E-U0 < 0, k2=ik; где
. Вероятность найти частицу в области 2 при E-U0 < 0, k2=ik; где 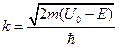 равна:
равна:
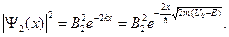
Дата добавления: 2015-02-07; просмотров: 2815;
