Измерение отклонений формы номинально плоских поверхностей деталей

Измерения отклонений от прямолинейности и плоскостности поверхностей деталей включают сравнение реального элемента (поверхности, профиля) с номинальным элементом, который называют исходной плоскостью или прямой, и оценку расхождений между ними (рис. 3.29).

Рис. 3.29. Принципиальная схема измерения отклонений формы

номинально плоских поверхностей

Исходную плоскость или прямую в используемых средствах измерений воспроизводят с помощью меры либо с помощью эталонного кинематического устройства.

В качестве исходной плоскости (прямой) можно использовать рабочие поверхности поверочной плиты, лекальной линейки, поверхность свободно налитой жидкости, луч света и прочее. Исходя из этого, в зависимости от способа задания исходной плоскости (прямой) различают механические, гидростатические, оптико-механические и оптические принципы и средства измерений.

Для осуществления операции сравнения применяют различные измерительные преобразователи или приборы, отличающиеся принципами измерений, конструктивным исполнением, функциональными возможностями. Это могут быть механические измерительные головки (индикаторы часового типа, рычажно-зубчатые измерительные головки, микрокаторы и др.), оптические и оптико-механические измерительные приборы, индуктивные, емкостные, пневматические измерительные преобразователи. По применяемому принципу измерения выделяют такие метолы измерения прямолинейности и плоскостности как механические, оптико-механические, интерференционные, электрические, гидравлические и пневматические.

В зависимости от способа сравнения реального элемента с исходным различают два базовых метода измерения:

- метод, основанный на измерении расстояний между реальным элементом и исходной плоскостью или прямой (f-метод);

- метод, основанный на измерении углов наклона локальных участков измеряемого реального элемента по отношению к исходной плоскости или прямой (d-метод).

Сущность первого метода состоит в том, что с помощью выбранного средства линейных измерений в необходимом числе контрольных точек реального элемента определяют расстояние Δ(x_i) от исходного элемента f₀(x) до контролируемого элемента f(x). Графически с учетом неидеальности исходного элемента это можно интерпретировать так, как показано на рис. 3.30.

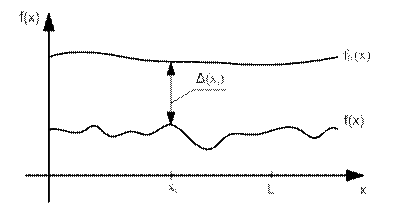
Рис. 3.30. Измерение отклонений формы номинально плоских

поверхностей деталей f-методом

Полученный таким образом массив результатов измерений Δ(x_i) (i = 1, 2, 3, …, n) подвергают математической обработке с использованием аналитических расчетов или (и) графических построений с целью определения искомого действительного значения отклонения формы контролируемой поверхности по отношению к вспомогательному номинальному элементу (прилегающей или средней прямой либо плоскости). При измерениях отклонений от плоскостности контрольные точки обычно располагают в узлах сетки, состоящей из продольных, поперечных и диагональных сечений.

Принципиальные особенности этого метода наиболее наглядно прослеживаются на примерах использования при измерениях для задания исходной поверхности (профиля) поверочных плит и поверочных линеек. Сравнение может производиться «на просвет» при контроле лекальными линейками или метод контроля «на краску» при проверке шаброванными плитами и линейками. При контроле линейками с широкими рабочими поверхностями используют концевые меры длины или измерительные головки (индикатор часового типа, микрокатор и др.). В качестве средств измерения отклонений или расстояний Δ(x_i) также могут использоваться приборы с электрическими (емкостными, индуктивными и др.), оптическими, пневматическими и любыми другими первичными измерительными преобразователями.

На практике часто используются поверочные линейки с широкими рабочими поверхностями, а непосредственное измерение размеров или отклонений Δ(x_i) осуществляется с помощью блоков концевых мер длины или измерительных головок.

Например, при измерении отклонения от плоскостности с помощью поверочной линейки и концевых мер длины на угловые точки устанавливают концевые меры длины одинакового размера чем определяют базу при измерении отклонений (рис. 3.31).

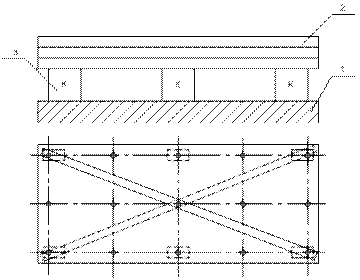
1 – измеряемая деталь; 2 – поверочная линейка; 3 – блок концевых мер длины

Рис. 3.31 – Измерение отклонения от плоскостности с помощью

поверочной линейки и концевых мер длины

На две базовые меры по диагонали устанавливают поверочную линейку и подбором блока концевых мер длины находят отклонение контрольной точки в середине диагонали. Затем устанавливают линейку по второй диагонали, опирая ее на известные меры в начальной угловой точке и середине, и с помощью подобранного блока концевых мер определяют отклонение во второй крайней угловой точке. По известным отклонениям четырех угловых точек установкой поверочной линейки во всех выделенных продольных и поперечных сечениях и подбором концевых мер определяют отклонения остальных намеченных точек. В итоге получают дискретную модель контролируемой поверхности в виде массива измеренных координат ограниченного количества контрольных точек, характерным образом расположенных на контролируемой поверхности. Произведя необходимую обработку (графическую, аналитическую или графоаналитическую) результатов измерений, находят отклонение от плоскостности контролируемой поверхности.

Процедура измерения с помощью поверочной линейки и измерительной головки аналогична описанной выше с той разницей, что измерения отклонений точек с помощью блоков концевых мер длины заменяются измерениями с помощью измерительной головки, а линейка опирается на регулируемые опоры. С помощью таких опор осуществляется предварительная выверка рабочей поверхности поверочной линейки так, чтобы показания измерительной головки по краям линейки были одинаковы. Схема измерения в этом случае выглядит следующим образом (рис. 3.32).

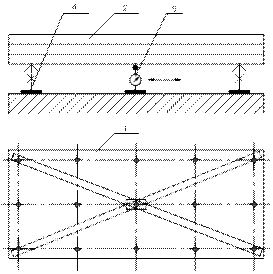
1 – измеряемая деталь; 2 – поверочная линейка;

3 – измерительная головка; 4 – регулируемая опора

Рис. 3.32. Измерение отклонения формы номинально плоской

поверхности с помощью поверочной линейки и измерительной головки

Метод измерения линейных отклонений часто реализуют с использованием поверочной плиты и измерительной головки, закрепленной в стандартной стойке или штативе, по схеме, представленной на рис. 3.33.

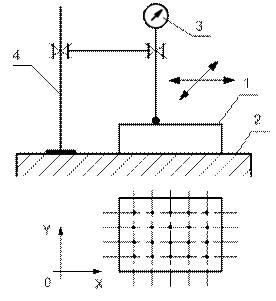
1 – измеряемая деталь; 2 – поверочная плита;

3 – измерительная головка; 4 – штатив (стойка)

Рис. 3.33. Измерение отклонения формы номинально плоской поверхности

с использованием поверочной плиты и измерительной головки

Реализация каждой из рассмотренных методик приводит к дискретной модели контролируемой поверхности.

Типичным представителем средств измерений, наиболее наглядно демонстрирующим суть методов, основанных на измерениях углов наклона, является микронивелир (рис. 3.34).

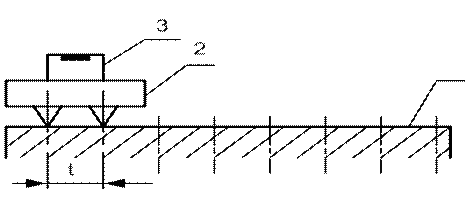
1 – измеряемая деталь; 2 – измерительный мостик (основание); 3 – уровень

Рис. 3.34. Измерение отклонения формы номинально плоской поверхности

с помощью микронивелира

Это средство измерений позволяет выполнять шаговые измерения отклонений от прямолинейности. Основание прибора имеет две опоры и на него установлен уровень (пузырьковая ампула в специальной оправе). Шаг измерения t определяется расстоянием между опорами основания. При реализации измерительной процедуры микронивелир размещают на контролируемой поверхности таким образом, чтобы опоры основания были установлены в контролируемых точках поверхности, расположенных на расстоянии одного шага измерения друг от друга. Затем последовательно (шаг за шагом) перемещают микронивелир, устанавливая его на все соседние пары контролируемых точек поверхности, и по шкале ампулы уровня определяют изменения угла наклона прибора.

В данном случае величиной, подвергаемой прямым измерениям, является угол между прямой, соединяющей точки опоры основания микронивелира, и горизонтальной плоскостью, касательной к эквипотенциальной поверхности гравитационного поля в одной из точек измерения.

Выполняемая после завершения измерительной процедуры дальнейшая простая, но довольно громоздкая обработка результатов измерений, включающая аналитические расчеты и графические построения, позволяет воспроизвести рельеф измеряемой поверхности и оценить искомое отклонение ее формы.

К этому же методу относятся также измерения с помощью электронных уровней, получивших широкое распространение на практике, измерения с использованием автоколлимационных средств измерений, а также коллиматоров и зрительных труб. При «оптических» реализациях непосредственно измеряемой величиной является угол между вектором энергетической оси светового пучка и его проекцией на плоскость, касательную к контролируемой поверхности в точке измерения.

Графическая интерпретация d-метода измерения с учетом неидеальности реализаций исходного элемента представлена на рис. 3.35.

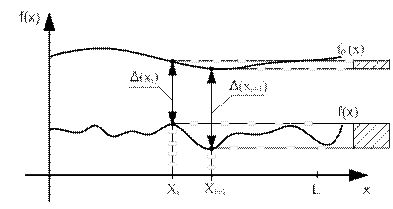
Рис. 3.35. Измерение отклонения формы номинально плоской

поверхности d-методом

На данном графике f₀(x) – функция, описывающая исходную (образцовую) поверхность (например, для микронивелира – эквипотенциальную поверхность гравитационного поля); f(x) – функция, описывающая контролируемую (реальную) поверхность. Как следует из этих графиков, непосредственно измеряемой величиной, по сути, является разность Δ(x_i+1) – Δ(x_i). При проведении измерений указанную разность определяют в необходимом числе контрольных точек поверхности (или непрерывно – при автоматизированных измерениях) и после необходимой обработки находят искомое отклонение формы контролируемой поверхности.