ИЗМЕРЕНИЕ КОНЦЕНТРАЦИИ
T=NTи ;
иT = Tи / 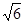
Точность измерения можно повысить за счет синхронизации, совместив со старт импульсом первый счетный импульс. Тогда
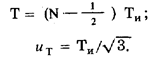
Такая точность приемлема, если Т >> Ти. При измерении длительности крутых фронтов и очень коротких импульсов используют стробоскопический и нониусный методы измерения временных интервалов.
Импульсные процессы могут иметь настолько сложную форму, что такие понятия, как амплитуда, длительность импульса и другие, становятся неопределенными. Что, например, можно сказать о параметрах импульса, показанного на рис. 108?
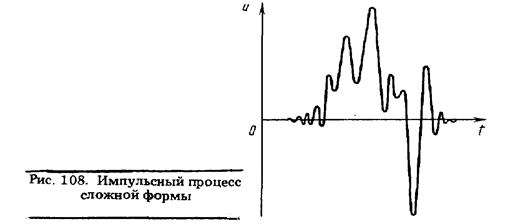
Для импульсных процессов сложной формы разработана система обобщенных параметров импульсов.
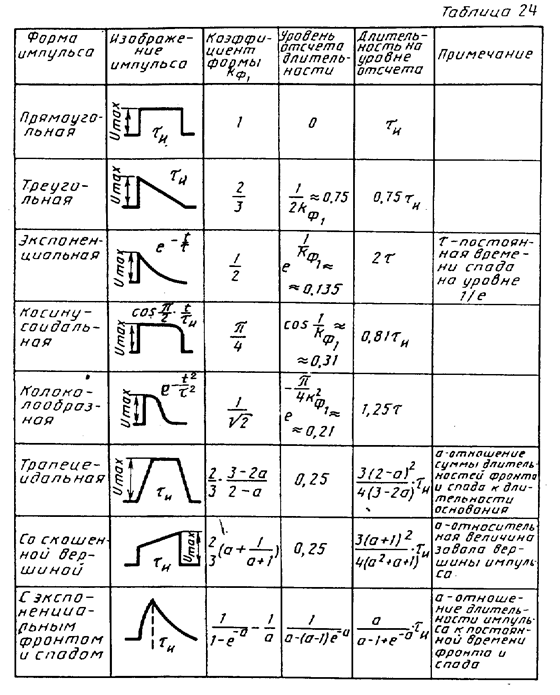
Под обобщенной амплитудой и длительностью импульса произвольной формы (без высокочастотного заполнения) понимаются амплитуда и длительность эквивалентного прямоугольного импульса, имеющего такую же площадь и энергию. Обобщенная амплитуда Um связана с максимальной амплитудой импульса Umax соотношением Um = Кф1 Umax, где Кф1— коэффициент формы, значения которого для импульсов наиболее распространенной формы приведены в табл. 24. Там же приведены выражения для обобщенных длительностей импульсов.
Обобщенная длительность фронта импульса произвольной формы (без высокочастотного заполнения) определяется как длительность фронта некоторого эквивалентного импульса с линейно нарастающим фронтом. При таком определении четко выражены начало и конец фронта, а скорость нарастания постоянна и равна отношению амплитуды к длительности фронта.
Понятия обобщенных мощности и длительности импульса с высокочастотным заполнением аналогичны. Ими целесообразно пользоваться во всех случаях, когда представляет интерес энергетическое воздействие импульса с высокочастотным заполнением.
Коэффициенты формы характеризуют отличие формы импульсов от прямоугольной. Чем больше их используется, тем полнее описание формы. Приборы, измеряющие обобщенные параметры импульсных процессов, называются интегральными измерителями параметров импульсов. Отечественной промышленностью они выпускаются в аналоговом и цифровом варианте.
5.3. ИЗМЕРЕНИЕ ПАРАМЕТРОВ СЛУЧАЙНЫХ ПРОЦЕССОВ
5.3.1. Измерение параметров стационарных случайных процессов
Процесс называется случайным, если при многократных повторениях он всякий раз протекает случайным образом.
Существуют два способа описания случайных процессов. При первом из них каждому текущему моменту времени t ставятся в соответствие случайные величины XiÎ{1,...,n} при втором — случайный процесс X(t) задается множеством своих реализации Xi(t) (рис. 109). Случайные величины Xi в каждом сечении t = const подчиняются определенному закону распределения вероятности. Если он одинаков для любого сечения, т. е. не зависит от времени, то процесс называется стационарным; в противном случае — нестационарным. Стационарные процессы обладают свойством эргодичности, заключающемся в том, что вероятностные характеристики, вычисленные по множеству реализации и по любой из них, равны между собой. Это позволяет при измерениях обходиться одной реализацией
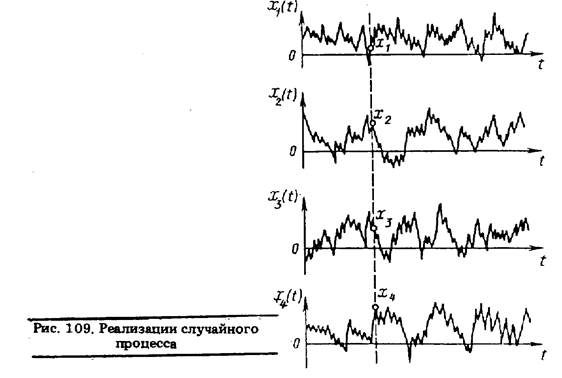 |
стационарного случайного процесса.
Исчерпывающая информация о случайном процессе содержится в его многомерной интегральной функции распределения вероятности
Fn(X1 , . . , Xn ; t1 , . . , tn ) = P{ X(t1) ≤ X1 , . . . ,X(tn) ≤ Xn},
характеризующей вероятность того, что в моменты времени ti случайные величины Xi, не превысят определенных своих значений, и в многомерной дифференциальной функции (плотности) распределения вероятности
pn (X1 , . . , Xn ; t1 , . . , tn )= 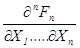
Применительно к одной реализации стационарного случайного процесса интегральная функция распределения вероятности F(X), определяемая как вероятность того, что значения X(t) лежат, ниже некоторого уровня Х (t) = Х = const (см. рис. 110), характеризуется относительным временем п  ребывания сигнала X(t) ниже этого уровня, т. е.
ребывания сигнала X(t) ниже этого уровня, т. е.
F(X) = P{ X(t) < X } = 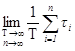
где Т — время измерения. На этом и основывается измерение F (X). Сигнал Х (t) подается на амплитудный селектор (см. рис. 111) с регулируемым порогом срабатывания Х ждущего одновибратора — триггера Шмитта, вырабатывающего прямоугольные импульсы единичной амплитуды (см. рис. 110), интегрирование которых позволяет найти оценку интегральной функции распределения вероятности по формуле ,
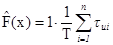
так как численное значение площади каждого i-го импульса равно его длительности tиi . Точность оценки тем выше, чем больше время измерения Т.
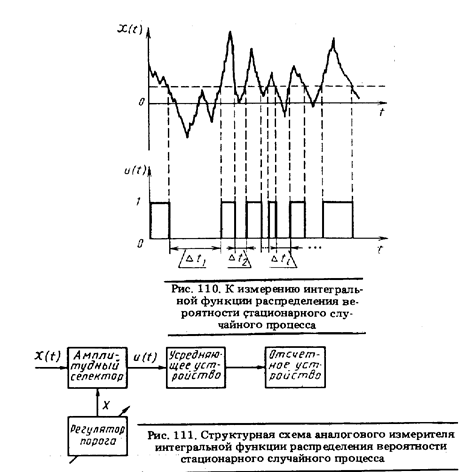
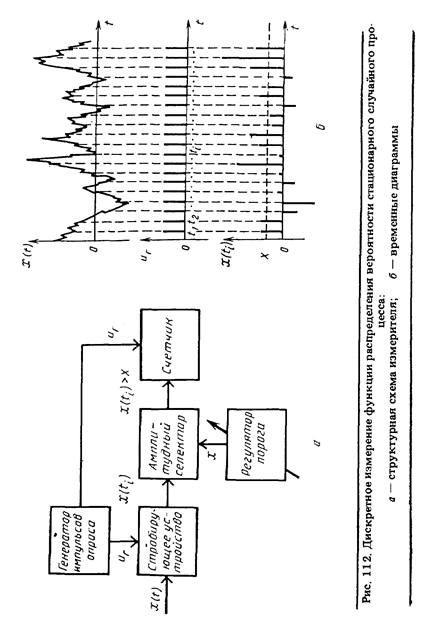
В дискретном варианте измерение функции распределения вероятности производится следующим образом. Стробирующее устройство (см. рис. 112, а) пропускает сигнал Х (t) только в моменты поступления на него импульсов опроса, вырабатываемых специальным генератором. В результате на амплитудный селектор поступают короткие импульсы, модулированные по амплитуде. Селектор представляет собой ограничитель, пропускающий только те импульсы, амплитуда которых больше порогового значения X. Число их подсчитывается счетчиком и позволяет получить оценку интегральной функции распределения вероятности по формуле
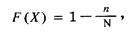
где n — показание счетчика; N — общее число импульсов опроса за время анализа Т. На рис. 112, б приведены временные диаграммы, иллюстрирующие измерение интегральной функции распределения вероятности стационарного случайного процесса этим методом.
 |
Плотность распределения вероятности стационарного случайного процесса,представленного одной реализацией, может быть выражена через относительное время пребывания сигнала Х [t) в интервале значений Х + ΔХ:
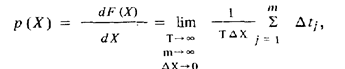
где обозначения ясны из рис. 113, а. Отсюда вытекает способ получения оценки плотности распределения вероятности
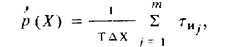
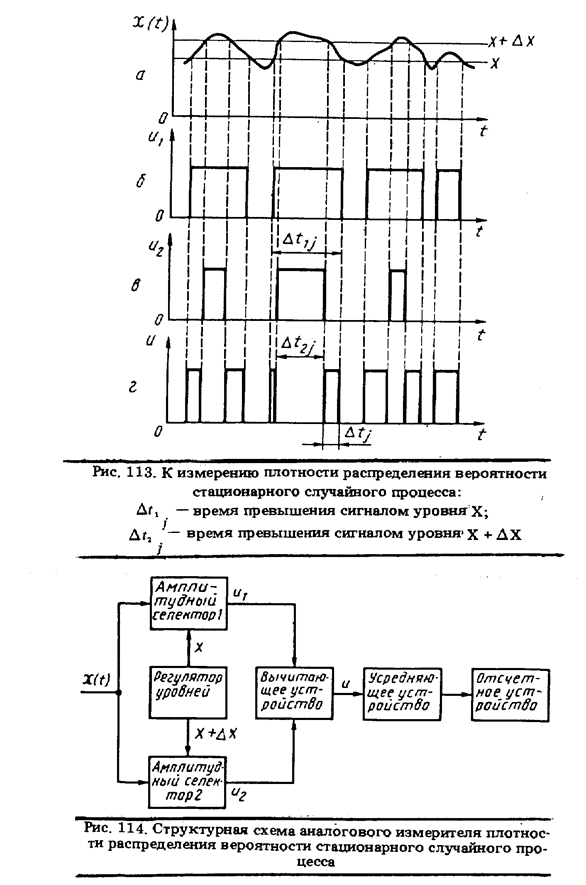
где tиi = Dtj могут рассматриваться как временные интервалы между фронтами импульсов, формируемых на время превышения сигналом X(t) уровней Х = const (см. рис. 113,6) и Х + DХ = const (рис. 113, в). Соответствующая структурная схема показана на рис. 114. Измеритель плотности распределения вероятности стационарного случайного процесса состоит из двух идентичных каналов, в которых вырабатываются прямоугольные импульсы единичной амплитуды, длительности которых в каждом канале равны, соответственно, времени превышения сигналом уровней Х и Х + DХ . Последние задаются регулятором уровней, обеспечивающим в то же время DХ = const. В устройстве вычитания формируются импульсы с единичной амплитудой и длительностью tиi (см. рис. 113, г), интегрирование которых позволяет получить в отсчетом устройстве оценку 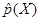 . Точность оценки тем выше, чем меньше DХ и чем больше время измерения Т.
. Точность оценки тем выше, чем меньше DХ и чем больше время измерения Т.
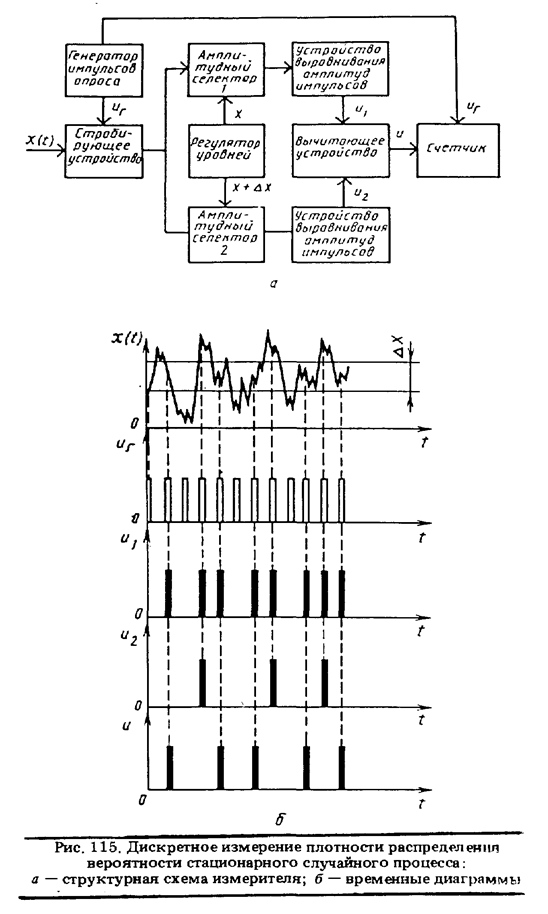
 При дискретном измерении плотности распределения вероятности стационарного случайного процесса подсчитывается разность между количеством импульсов опроса, поступивших из двух идентичных каналов с разными пороговыми уровнями. Подробно работу измерителя можно проанализировать по рис. 115. Оценка плотности распределения вероятности получается по формуле
При дискретном измерении плотности распределения вероятности стационарного случайного процесса подсчитывается разность между количеством импульсов опроса, поступивших из двух идентичных каналов с разными пороговыми уровнями. Подробно работу измерителя можно проанализировать по рис. 115. Оценка плотности распределения вероятности получается по формуле
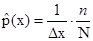
где по-прежнему n — показание счетчика, а N — общее число импульсов опроса за время анализа Т.
На практике часто ограничиваются измерением более простых параметров — моментов или числовых характеристик законов распределения вероятности стационарных случайных процессов.
Первый начальный момент (среднее значение или математическое ожидание стационарного случайного процесса)
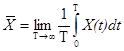
представляет собой постоянную составляющую сигнала (см. рис. 116). Получение оценки среднего значения
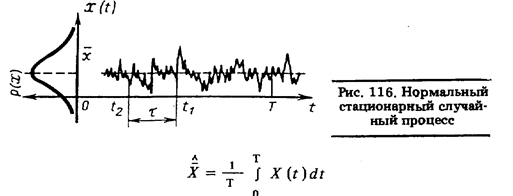
сводится к усреднению сигнала за время измерения Т. Оно выполняется 'всевозможными фильтрами нижних частот (например, интегрирующими RC-цепочками или интегрирующими звеньями, построенными на основе использования усилителей постоянного тока с глубокой отрицательной обратной связью), магнитоэлектрическими механизмами, инерционными системами, устройствами с демпфированием и т. п. В цифровом варианте оценка среднего значения получается путем усреднения не самого сигнала, а его дискретных значений
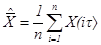
где t — интервал между выборками из реализации Х (t), а п — число выборок.
Второй начальный момент (средняя мощность стационарного случайного процесса)
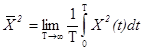
характеризует энергетический уровень сигнала. Для получения оценки
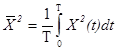
обычно используется квадратичное детектирование сигнала с последующим усреднением за время измерения Т. Среднее значение выходного напряжения после квадратичного Преобразователя можно измерять магнитоэлектрическим прибором. Проще всего задача измерения  решается с помощью вольтметров среднеквадратического значения, имеющих открытый вход. Показание такого вольтметра равно
решается с помощью вольтметров среднеквадратического значения, имеющих открытый вход. Показание такого вольтметра равно 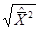 и не зависит от формы измеряемого напряжения.
и не зависит от формы измеряемого напряжения.
Второй центральный момент (дисперсия стационарного случайного процесса)
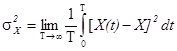
характеризует среднюю мощность переменной составляющей (флюктуаций) сигнала. Для получения ее оценки
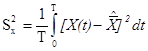
также может быть использован вольтметр среднеквадратического значения, но с закрытым входом. Показания такого вольтметра будут соответствовать стандартному отклонению
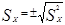
Можно также воспользоваться соотношением
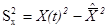
в котором оценка средней мощности, измеряемая цифровым прибором,
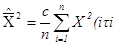
где с = const.
Мерой неопределенностизначений стационарного случайного процесса служит энтропия, для оценки которой
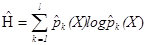
Используются l дискретных значений плотности распределения вероятности.
Мерой статистической связи между значениями стационарного случайного процесса без постоянной составляющей в моменты времени t1 и t2= t1 -t служит смешанный центральный момент 2-го порядка 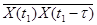 , называемый корреляционным. Вероятностно-статистические характеристики стационарного случайного процесса не зависят
, называемый корреляционным. Вероятностно-статистические характеристики стационарного случайного процесса не зависят
от времени, поэтому t1 можно выбрать произвольно; приняв t1= t. Тогда корреляционный момент будет зависеть только от τ:
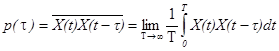 (29)
(29)
С переходом от фиксированного времени к текущему корреляционный момент стал функцией.
Определенная выражением (29) корреляционная функция обладает следующими свойствами.
1. При t= 0 корреляционная функция р(0)=Х(t)X(t)= Х2 = 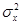 максимальна и равна дисперсии стационарного случайного процесса (рис. 117). Если измеряемой физической величиной является, например, сила тока i(t), то r (0) =
максимальна и равна дисперсии стационарного случайного процесса (рис. 117). Если измеряемой физической величиной является, например, сила тока i(t), то r (0) = 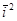 — полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае, когда процесс имеет постоянную и переменную составляющие, r(0) =
— полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае, когда процесс имеет постоянную и переменную составляющие, r(0) = 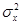 +
+ 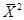 где
где 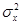 и
и 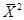 мощности, соответственно переменной и постоянной составляющих.
мощности, соответственно переменной и постоянной составляющих.
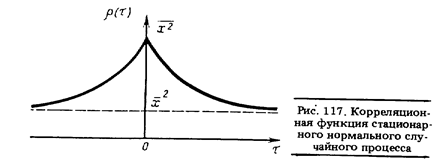
Максимальное значение корреляционной функции при t = 0 объясняется тем, что статистическая связь между неразличимыми по времени значениями X(t) является наибольшей.
Корреляционную функцию часто нормируют по ее максимальному значению: r (τ) = r (τ) / r (0). Тогда r (0) = 1.
2. Корреляционная функция является четной, т. е. р (τ) = r (—τ). Это можно показать, выбрав в качестве текущего момент времени t2 = t и обозначив t1= t2 + τ (см. рис. 116). Спектр корреляционной функции состоит, следовательно, только из косинусоидальных составляющих.
3. При τ→∞ r (τ) → 0 (у процессов с постоянной составляющей — к 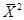 ), если в X(t) нет детерминированной составляющих.
), если в X(t) нет детерминированной составляющих.
4. Корреляционная функция r(τ) монохроматического колебания являетсякосинусоидой с такой же частотой. Доказательство этого важного свойства приведено в примере 55, а важным следствием является то, что при корреляционном преобразовании теряется информация о фазовой структуре процесса.
5. Корреляционная функция суммы независимых процессов равна сумме их корреляционных функций. Вместе с предыдущим это свойство используется в оптимальной фильтрации для суммирования гармоник сигнала в момент τ= 0.
6. Корреляционная функция связана со спектральной плотностью мощности случайного процесса прямым и обратным преобразованиями Фурье:
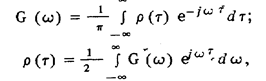
которые с учетом четности корреляционной функции могут быть переписаны в виде:
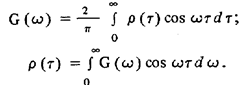
Это положение известно как теорема преобразования Винера-Хинчина. Таким образом, энергетический спектр G(ω), как и корреляционная функция р (τ ), может служить неслучайной характеристикой случайного процесса.
На практике из-за конечности времени усреднения Т определяется не сама корреляционная функция, а ее оценка
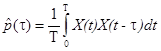
что учитывается иногда внесением в результат измерения поправки. Представление о ней можно получить из следующего примера.
Пример 55.Найти корреляционную функцию гармонического колебания Х (t) = Xmax. sin (ωt + φ) и поправку при ее измерении с интервалом усреднения Т.
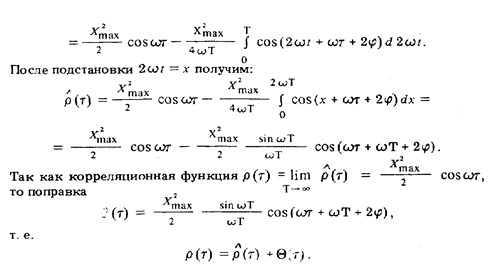 Решение.Оценка корреляционной функции
Решение.Оценка корреляционной функции
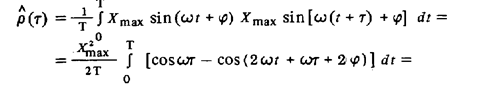
Таким образом, поправка Θ (τ ) является гармонической функцией той же частоты, что и р (τ), но с начальной фазой, содержащей информацию о фазе гармонического колебания X(f) (рис. 118). Поправка Θ (τ ) особенно значительна на низких частотах и убывает с
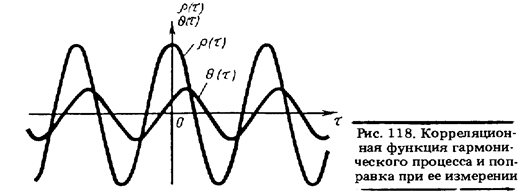
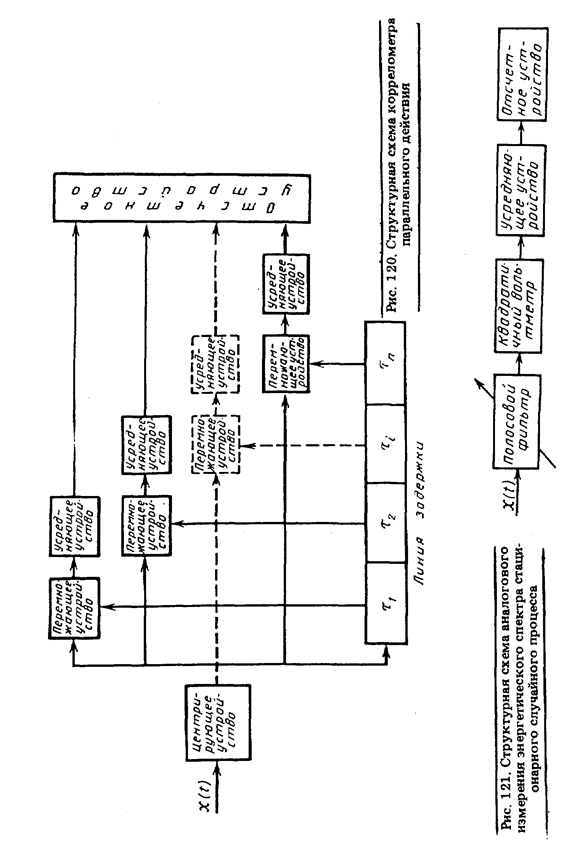
увеличением времени усреднения Т. При τ → 0 корреляционная функция сложного сигнала р(τ) → р(0), так как поправки суммируются с разными фазами (в том числе и с противоположными).Средства измерений, предназначенные для определения корреляционной функции, называются коррелометрами. Различают коррелометры последовательного и параллельного действия. Структурная схема простейшего коррелометра последовательного действия приведена на рис. 119. Значения корреляционной функции получают, изменяя время задержки сигнала t. В многоканальном коррелометре параллельного действия осуществляется одновременное вычисление значений корреляционной функции при различных значениях t, тем самым сокращается время измерения. Упрощенная структурная схема такого коррелометра показана на рис. 120.
В цифровых коррелометрах все операции производятся с дискретными значениями сигнала. Современные цифровые анализаторы статистических характеристик являются, как правило, многофункциональными приборами, позволяющими измерять все основные параметры стационарных случайных процессов. В их число входит и энергетический спектр G(ω) , для определения которого цифровой коррелометр дополняется вычислительным устройством, осуществляющим быстрое преобразование Фурье. Энергетический спектр G(ω), представляющий собой спектральную плотность мощности (среднюю мощность сигнала, приходящуюся на единицу полосы частот), может измеряться и непосредственно спектроанализатором, к выходу которого подключается вольтметр среднеквадратического
значения с закрытым входом. В этом случае оценка энергетического спектра
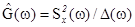
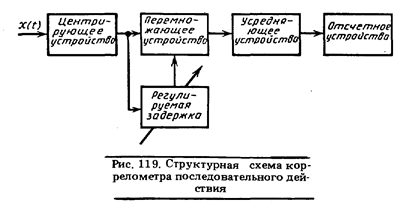 где
где 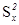 — оценка средней мощности, выделяемой на сопротивлении 1 Ом спектральной составляющей сигнала с частотой ω, соответствующей средней частоте узкополосного фильтра с шириной полосы пропускания Δω. Эквивалентная структурная схема измерения показана на рис. 121. От спектрального анализа детерминированных процессов, являющегося линейным преобразованием, она отличается наличием квадратичного преобразования и усреднения.
— оценка средней мощности, выделяемой на сопротивлении 1 Ом спектральной составляющей сигнала с частотой ω, соответствующей средней частоте узкополосного фильтра с шириной полосы пропускания Δω. Эквивалентная структурная схема измерения показана на рис. 121. От спектрального анализа детерминированных процессов, являющегося линейным преобразованием, она отличается наличием квадратичного преобразования и усреднения.
 |
ИЗМЕРЕНИЕ КОНЦЕНТРАЦИИ
6.1. ИЗМЕРЕНИЯ В ХИМИЧЕСКОМ АНАЛИЗЕ
Концентрация, наряду с температурой и давлением, является основным параметром, определяющим термодинамическое состояние системы. С другой стороны, концентрация компонентов является одним из свойств вещества. Примером может служить влажность, которую рассматривают даже как самостоятельную физическую величину. В действительности влажность определяется концентрацией воды в газообразных, жидких или твердых смесях. В качестве другого примера можно привести железо. В зависимости от концентрации в нем углерода получается целый набор материалов от чистого железа до чугунов различных марок. Присутствие в железе дополнительно ряда других металлов в качестве примесей, прежде всего хрома, никеля, марганца и т. п. позволяет получить набор различных марок стали.
Концентрация — величина, характеризующая относительное содержание данного компонента в многокомпонентной термодинамической системе. В химическом анализе такой термодинамической системой является анализируемый объект. Химический анализ в общем случае состоит из качественного и количественного анализов. Задачей качественного анализа является определение химической природы компонентов, из которых состоит анализируемый объект. Задачей количественного анализа является определение концентрации этих компонентов. При этом под компонентами вещественной системы понимают атомы, ионы, молекулы, радикалы и макромолекулы, а в общем виде — химические элементы и соединения. Употребляя термин „химический анализ", подчеркивают его основную цель — определение химического состава *, включая определение концентрации компонентов, составляющих данную вещественную систему. В то же время методы, используемые для достижения этой цели, могут быть как химическими, так и физико-химическими или физическими.
· Часто встречается термин "измерение состава". Использование этого термина не рекомендуется, так как состав не относится к физическим величинам. То же самое относится к термину "содержание компонента", употребляемому вместо термина "концентрация компонента".
·
Получение достоверных результатов о концентрации компонентов в анализируемом объекте требует решения проблем воспроизведения единицы концентрации, обеспечения единства измерения концентрации и контроля правильности полученных результатов. Решение всех перечисленных выше проблем возможно только в тесной взаимосвязи метрологических правил, изложенных в предыдущих разделах, с теоретическими основами химического анализа. Принципиальным при этом является положение о том, что теоретические основы аналитической химии едины и нет отдельно теории качественного и теории количественного анализа. Отсюда следует, что для выявления специфики концентрации как измеряемой физической величины необходимо рассмотреть с позиций метрологии обе составляющее" химического анализа.
Для осуществления измерения как физического эксперимента необходимы объект и средство измерений. Однако этих двух составляющих недостаточно для проведения измерения. Связующим звеном, превращающим измерение в физический процесс, является метод измерения. Для наглядности поясним это рис. 133.

В дальнейшем будем исходить из следующих определений принципа, метода и методики измерения.
Принцип измерения — научная основа метода измерения.
Метод измерения — комплекс теоретических положений и практических операций в общем виде, используемых при проведении измерений в соответствии с принятым принципом.
Методика измерений — детальное описание практических операций и теоретических положений, используемых при проведении измерений в соответствии с принятым методом.
Перед обсуждением особенностей измерений при проведении химического анализа введем временно следующие допущения:
1. Анализу подвергается весь образец, а не отобранная специальным образом проба.
2. Образец гомогенен и все анализируемые компоненты находятся в аналитически активной форме.
Введение таких допущений преследует цель свести химический анализ к измерению, благодаря временному и, естественно, чисто условному исключению из рассмотрения таких этапов химического анализа, как пробоотбор и пробоподготовка. Эти допущения необходимы, чтобы в центре обсуждения вначале оставались бы только вопросы, связанные с видом физических—величин, измеряемых при проведении как количественного, так и качественного анализов.
Принцип измерения, характеризуется физическим явлением, возникающим в результате взаимодействия какого-либо внешнего возмущающего фактора на анализируемое вещество. В результате воздействия происходят взаимодействия внешних возмущающих факторов с компонентами вещества, классифицируемые как упругие и неупругие взаимодействия*.
Упругие взаимодействия. В качестве возмущающих факторов при упругих взаимодействиях выступают электромагнитное излучение или потоки элементарных частиц. Условием упругих взаимодействии является выполнение требования
S D E 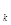 = 0,
= 0,
где E 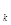 — кинетическая энергия.
— кинетическая энергия.
Следовательно, энергия излучения в ходе взаимодействия не изменяется. Внутренняя энергия компонентов анализируемого вещества также не изменяется. В то же время происходит изменение пространственной структуры излучения, обусловленное структурой вещества. В результате упругого взаимодействия происходит лишь изменение направления излучения. Измеряемая при этом величина w является преимущественно тригонометрической функцией распределения энергии:
w = f (sin I 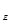 ),
),
где i 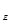 — интенсивность.
— интенсивность.
В качестве примера в табл. 26 приведены методы анализа, основанные на упругих взаимодействиях (волновых явлениях) . Принципы измерения в этих методах анализа основываются на таких физических явлениях, как преломление (Пр), дифракция — интерференция (Д/И), отражение (Отр), поляризация (Пол) и рассеяние (Рс).
* В основу изложения данного вопроса положены обобщения, полученные К. Данцером с соавторами.
Неупругие взаимодействия. Неупругие взаимодействия составляют основу значительно большей группы методов анализа. При этом виде взаимодействия анализируемого вещества с внешним источником энергии происходит как изменение энергии, поступающей от внешней системы, так и
изменение внутренней энергии вещества. Однако соблюдается условие
S D E 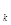 = -S D U ,
= -S D U ,
т. е. каждому изменению кинетической энергии (E 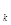 ) однозначно соответствует изменение потенциальной энергии (U). В табл. 27 приведены методы анализа, основанные на неупругих взаимодействиях.
) однозначно соответствует изменение потенциальной энергии (U). В табл. 27 приведены методы анализа, основанные на неупругих взаимодействиях.
Важно отметить, что конкретные значения DU и соответственно D E 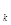 характеризуют химическую природу компонентов анализируемого вещества. В то же время сумма всех одинаковых квантов DЕ, определяющая интенсивность, закономерно связана с количеством каждого компонента.
характеризуют химическую природу компонентов анализируемого вещества. В то же время сумма всех одинаковых квантов DЕ, определяющая интенсивность, закономерно связана с количеством каждого компонента.
Таблица 27
| Виды внутренней энергии | Методы анализа | |||||
| Объекты анализа | ||||||
| Атомы, ионы | Молекулы | Агрегатированные системы | Реакционные системы | |||
| Перенос (массы и заряда) | Maсс - спектроскопия | - | - | |||
| Ядерная энергия: ядерный момент уровни нуклонов энергия связи ядра | ЯМР - спектроскопия Спектроскопия Мессбауэра | - | - | |||
| Активационный анализ. | - | |||||
| Энергия электронов: момент электрона уровни электронов Энергия ионизации | ЭПР – спектроскопия Рентгеновская и электроннаяспектроскопия | - - - | - - - | |||
| Атомная спектроскопия | Спектроскопия в видимой и УФ областях | |||||
| Энергия молекулы: Энергия вращения Колебательная энергия Энергия диссоциации | - - - | Микроволновая ИК - спектроскопия и комбинационное рассеяние | - | - | ||
| Энергия решетки | - | - | Термический анализ | - | ||
| Энергия реакции: химический потенциал электрохимический потенциал | - - | - - | - - | Химические методы анализа Электрохимические методы анализа | ||
Формулы
wQ = f(Q) = j(ΔE); (37)
ωc = F(c) G(I∆E) (38)
являются уравнениями связи между измеряемыми величинами w, соответствующими значениями энергии D Е (D Ek или DU) и I 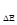 , и аналитической информацией на основе какого-либо механизма взаимодействия. Эти двауравнения составляют теоретическую основу химического анализа. Именно в этих уравнениях со всей полнотой проявляется отмеченная выше общность количественного и качественного анализов.
, и аналитической информацией на основе какого-либо механизма взаимодействия. Эти двауравнения составляют теоретическую основу химического анализа. Именно в этих уравнениях со всей полнотой проявляется отмеченная выше общность количественного и качественного анализов.
Обозначим через Q величины, характеризующие природу компонентов и являющиеся при этом физическими свойствами конкретных компонентов, а через с — их концентрации. Именно такой смысл имеют Qи с в уравнениях (37), (38).
Конкретные значения физических величин (Q), используемых при проведении качественного анализа, а также концентрации компонентов (с) при проведении количественного анализа получают из уравнений связи этих величин в результате преобразования уравнений (37), (38):
Q = j (wQ ) (39)
с=Ф (w 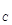 ) (40)
) (40)
При проведении количественного анализа уравнения связи (40), как правило, не известны. Поэтому для их установления используют процедуру, названную градуировкой. Следует отличать градуировку, рассмотренную в разд. 4.5.1 как процедуру передачи размера единицы физической величины, от градуировки как способа нахождения уравнения связи между отличающимися физическими величинами. В последнем случае, используя вещества с известными значениями концентрации, экспериментально определяется зависимость (40).
Особое значение для метрологии имеют те редкие случаи, когда указанные уравнения связи известны в виде строгих математических уравнений, которые составляют теоретическую основу особой категории методов анализа — абсолютных методов анализа. В этом случае концентрация рассчитывается по измеренным значениям физических величин, входящих в конкретные уравнения связи. При этом отпадает необходимость в построении градуировочной характеристики.
Информацию о качественном составе выражают константами веществ Q 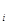 . При этом однородные константы можно расположить по их значениям от Q
. При этом однородные константы можно расположить по их значениям от Q 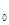 до Q
до Q 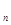 .Такое последовательное расположение классифицируют как одномерную аналитическую информацию (рис. 134, а). Типичным примером такой информации служат длины волн, отдельных элементов в спектре. В этом случае при проведении качественного анализа задачей измерения является обнаружение в соответствующем интервале спектра искомых конкретных длин волн. Результат качественного анализа представляется в форме ответа "да—нет".
.Такое последовательное расположение классифицируют как одномерную аналитическую информацию (рис. 134, а). Типичным примером такой информации служат длины волн, отдельных элементов в спектре. В этом случае при проведении качественного анализа задачей измерения является обнаружение в соответствующем интервале спектра искомых конкретных длин волн. Результат качественного анализа представляется в форме ответа "да—нет".
Одномерная аналитическая информация встречается и при проведении количественного анализа. Например, при определении концентраций какого-либо компонента, который характеризуется константой Q 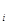 , (рис. 134, б).
, (рис. 134, б).
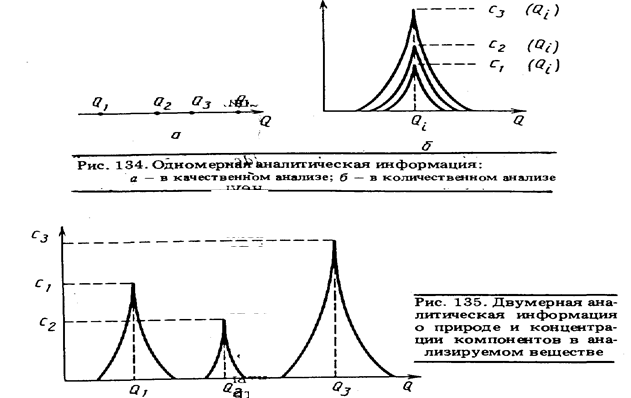
Если представить графически зависимость серии однородных характеристических величин Q 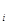 , и соответствующих им интенсивностей w
, и соответствующих им интенсивностей w 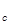 , являющихся согласно (40) функцией концентрации, то взаимосвязь этих параметров дает регистрограмму (спектрограмму, хроматограмму, полярограмму). Такие регистрограммы являются двумерной аналитическойинформацией, содержащей одновременно данные как о природе, так и о концентрации компонентов (рис. 135). Этот пример служит еще одной иллюстрацией неразрывной связи количественного и качественного анализа. Обнаружение сигналов при перемещении по оси Q соответствует качественному анализу, а измерение w
, являющихся согласно (40) функцией концентрации, то взаимосвязь этих параметров дает регистрограмму (спектрограмму, хроматограмму, полярограмму). Такие регистрограммы являются двумерной аналитическойинформацией, содержащей одновременно данные как о природе, так и о концентрации компонентов (рис. 135). Этот пример служит еще одной иллюстрацией неразрывной связи количественного и качественного анализа. Обнаружение сигналов при перемещении по оси Q соответствует качественному анализу, а измерение w  при фиксированных значениях Q
при фиксированных значениях Q 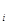 , дает данные о концентрации, т. е. относится к количественному анализу.
, дает данные о концентрации, т. е. относится к количественному анализу.
Для получения достоверных результатов метод химического анализа должен отвечать следующим требованиям.
1. Результаты измерений не должны быть искажены, т. е. измеряемая величина qa должна соответствовать характеристической константе компонента А. Это означает, что метод анализа должен быть избирательным (селективным) по отношению к этому компоненту. В таком случае мешающее влияние других компонентов, вызывающих появление систематической погрешности, может быть сведено к минимуму.
2. Средства измерений должны обеспечивать требуемую точность. При небольших концентрациях компонентов метод анализа в этом случае должен иметь высокую чувствительность, которая определяется следующим образом:
E= F'(c) =dw 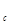 /dc.
/dc.
Все многообразие упругих и неупругих взаимодействий можно свести к нескольким основополагающим, как это представлено, например, на рис. 136, чтобы затем рассмотреть физические величины, охватываемые каждым из выделенных видов взаимодействий. Такой подход позволяет представить все многообразие аналитических методов в виде целостной системы.*
Методы анализа, основанные на химических реакциях. В общем виде химическую реакцию можно представить уравнением
аА + bВ  = gC + dD,
= gC + dD,
Где А, В, С, D — исходные компоненты и продукты реакции соответственно; а, b, g, d, -стехиометрические коэффициенты реакции.
На основании измерения хода химической реакции, определения концентрации продуктов реакции и связанных с этим изменений термодинамических характеристик системы получают информацию о химической природе и концентрации компонентов анализируемого вещества (рис. 137).
Химические реакции при определённых условиях составляют основу абсолютных методов измерения концентрации. Это предопределяет их непреходящее значение для воспроизведения единиц концентрации. В табл. 28 указан перечень физических величин, подлежащих измерению при проведении химических методов анализа.
——————————
* См. Данцер К., Тан Э., Мольх Д. Аналитика: Системат. обзор.
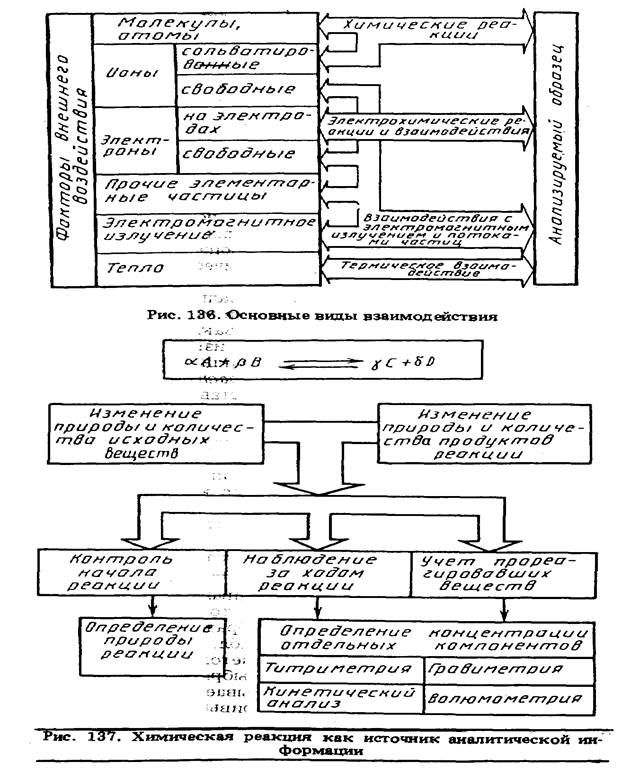
Таблица 28
Функциональная зависимость. 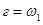
| ||
| Физические величины | Примечание | |
| Масса m | R- универсальная газовая постоянная | |
| Объем V | Т- температура | |
| Давление r | Р= cRT | |
| Скорость реакции k | k = dv/dt | |
| Время реакции t |
Рассмотрим один из принципов, используемый в методах анализа, основанных на химических реакциях. Остановим свой выбор на титриметрии, являющейся примером использования самых разнообразных физических свойств при решении аналитических задач.
Принцип титриметрического анализа основан на скачкообразном изменении ряда свойств в момент окончания химической реакции. Метод анализа заключается в измерении объема раствора реагента с точно "известной концентрацией, необходимого для проведения реакции с определяемым ионом до ее полного завершения. Уравнение связи для общего случая прямого титрования представляет собой следующее выражение:
yA = 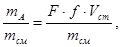
где у 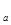 - концентрация, выраженная в массовой доле; mA = F • f • V
- концентрация, выраженная в массовой доле; mA = F • f • V 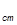 - масса определяемого компонента; m
- масса определяемого компонента; m 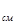 -масса смеси;
-масса смеси; 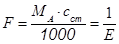 - стехиометрический фактор; сст - молярная концентрация титранта ; f = c
- стехиометрический фактор; сст - молярная концентрация титранта ; f = c 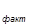 /с
/с 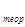 — поправочный коэффициент; V
— поправочный коэффициент; V 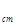 — объем титранта, затраченный для достижения точки эквивалентности.
— объем титранта, затраченный для достижения точки эквивалентности.
Для установления конечной точки титрования используют измерения самых разнообразных свойств. Представление об этих свойствах дает табл. 29, в которой представлен обзор инструментальных методов титрования. Графическая зависимость изменения выбранного свойства от объема добавляемого титранта называется кривой титрования. На рис. 138 показаны примеры кривых титрования.
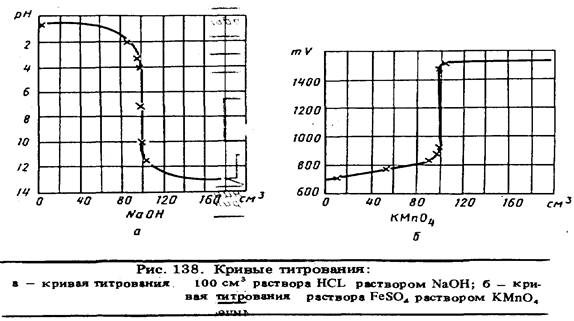
Важно подчеркнуть, что в методах титрования измеряемой величиной является объем реагента, а остальные перечисленные в табл. 29 величины служат лишь для точного определения объема в конечной точке титрования, т. е. они используются в данном методе анализа только для индикации.
Методы анализа, основанные на электрохимических реакциях. Основу электрохимических методов составляют неспецифические процессы, протекающие на электродах, а также специфические процессы, обусловленные электрохимическими реакциями (рис. 139). Эта группа методов также характеризуется большим разнообразием физических свойств, используемых как для качественного анализа, так и для определения концентрации. Те физические величины, которые входят в уравнение связи, подлежат измерению при проведении анализа. В табл. 30 приведен перечень таких электрических величин.
Методы анализа, основанные на термических процессах. Основу термических процессов составляет изменение энтальпии (ΔH):
ΔH = Cq 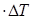 = m · cq ·Δ T.
= m · cq ·Δ T.
Оно является результирующим и включает все энтальпийные вклады анализируемой смеси, перечисленные в табл. 31. В зависимости от условий эксперимента различают энтальпиметрические и термометрические способы анализа, что нашло отражение в классификации термических методов анализа, представленных на рис. 140.
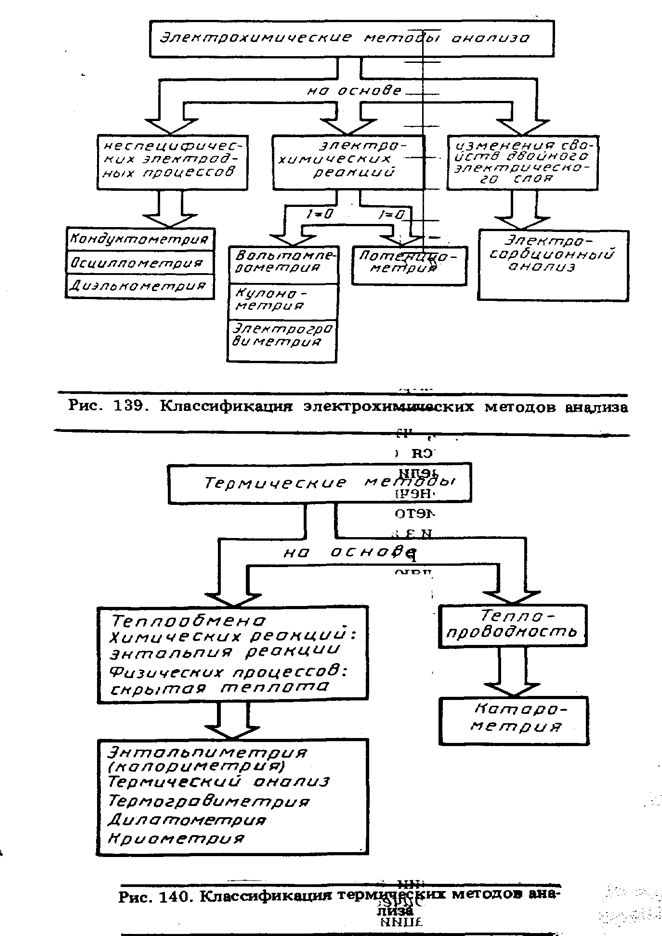
Таблица 29
| Метод титрования | Аналитическая функция | Измеряемое свойство (величина) | |
| 1. Оптические методы | |||
| 1.1. | Колориметрический | 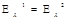
| Экстинкция (Ε 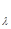 ) )
|
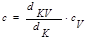
| |||
| 1.2. | Фотометрический | 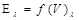
| Экстинкция |
| 1.3. | Флуориметрический | IF= 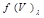
| Интенсивность флуоресценции (IF) |
| 1.4. | Турбидиметрический | ESλ= 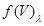
| Кажущаяся экстинкция (ЕS,λ) |
| 1.5. | Нефелометрический | FES= 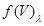
| Интенсивность рассеянного света (фез) |
| 1.6. | Поляриметрический | a= 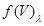
| Угол (вращательная способность растворов a) |
| 1.7. | Интерферометрический | nD - nD= 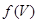
| Показатель преломления (nD) |
| 1.8. | Пламенно-фотометрический | I= 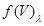
| Интенсивность излучения (I) |
| 2. Электрохимические методы | |||
| 2.1. | Кондуктометрический | K=f(V) | Электропроводность (к) |
| 2.2. | Осциллометрический | Yw=f(V) | Активная составляющая проводимости ячейки (Yw) |
| Yb=f(V) | Реактивная составляющая проводимости ячейки (Yb ) | ||
| 2.3. | Диэлькометрия | е=f(V) | Диэлектрическая проницаемость (е ) |
| 2.4. | Потенциометрический | E=f(V) 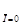
| Потенциал электрода (Е} |
| 2.5. | Амперо метрический | I=f(V)E=0 | Предельный диффузионный ток (/) |
| 2.6. | Вольт-амперетрический | E=f(V)i | Потенциал электрода (Е) |
| 3. Термические методы | |||
| 3.1. | Термометрический | T=f(V) | Температура (Т) |
| 3.2. | Дифференциально- термометрический | D T=f(V) | Температура |
| 3.3. | Энталъпиметрический | DH= f(V) | Энтальпия (DH) |
| 3.4. | Криоскопический | DT= f(V) | Температура |
| 3.5. | Дилатометрический | l = f(V) | Длина (l) |
| 4. Прочие методы | |||
| 4.1. | Вискозиметрический | tF1= f(V) | Время истечения (tF1) |
| 4.2. | Сталагмометрический | tTn= f(V) | Время падения капли (tTn ) |
| 4.3. | Радиометрический | Z= f(V) | Радиоактивность (скорость счета Z в импульсах в секунду) |
| 4.4. | Магнитометрический | х= f(V) | Магнитная проницаемость (х) |
| 4.5. | Акустический | n= f(V | Скорость звука (n) |
Таблица 30
| Измеряемая величина | Функциональная зависимость | Обозначение |
| Напряжение U | ||
| Потенциал электрода Е | ||
| Сила тока I | ||
| Плотность тока I | i= I/S | S - поверхность электрода |
| Сопротивление R | R = U /I | |
| Удельное сопротивление s | s = RS/d | d - расстояние между электродами |
| Проводимость G | G = 1 / R | |
| Удельная электропроводность к | к = 1/ s | |
| Импеданс Z | = U Z/ I~ | |Z| — кажущееся сопротивление |
| Z=Zw+jZb | |Zw| — действительное сопротивление | |
|Z| = 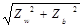 - -
| |Zb|— реактивное сопротивление | |
| Zb = RL - Rc | RL - индуктивное сопротивление | |
| RL =wL | Rc — емкостное сопротивление | |
| rc= 1/wC | С — емкость | |
| w — частота переменного тока | ||
| Проводимость переменного тока Y | Y = 1/Z | |
| Количество электричества | Q =I × t | t - время |
| Емкость С | C=Q/U | |
| Диэлектрическая проницаемость (относительная) е | ||
| Тангенс угла диэлектрических потерь tg d |
Таблица 31
| Измеряемая величина | Функциональная зависимость | Обозначение | |
| Энтальпия D H | 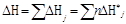
| DH* | — молярная энтальпия |
| DH пл | - энтальпия плавления (кристаллизации) | ||
| DH исп | — энтальпия возгонки | ||
| DH пр | - энтальпия превращения щения | ||
| DH разб | - энтальпия разбавления | ||
| DH шм | — энтальпия смесения | ||
| DH рк | — энтальпия реакции | ||
| Температура T | |||
| Количество теплоты Q | Q = Cq • DT = m • Cq DT | Сq cq | - теплоемкость - удельная теплоемкость |
| Теплопроводность lq | lq =Q/( I• DT ) |
Так как всякое изменение в вещественной системе связано с изменением энтальпии, особенно при химических реакциях, термические методы анализа нашли широкое распространение. Для качественного анализа особый интерес представляют определяемые термометрические точки, в которых происходят существенные изменения энтальпии. Температурный сдвиг этих точек используют в количественном анализе. Примером такого метода анализа является криометрия. В табл. 31 представлен перечень физических величин, подлежащих измерению методами анализа, основанными на термических процессах.
Регистрацию изменений агрегатного состояния, измерение энтальпии фазовых переходов и энтальпий реакций обычно производят по диаграммам, представляющим зависимость температуры анализируемого вещества от количества подводимого или отводимого тепла (рис. 141). Часто вместо Т - Н
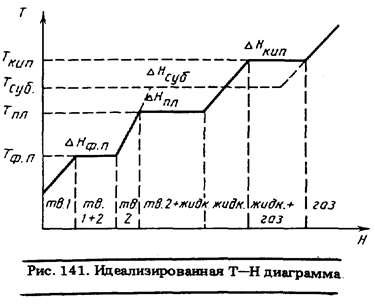
диаграммы строят Т - t диаграмму, обеспечивая для этого постоянство скорости теплоотвода.
В самое последнее время предложено использовать энтальпию для идентификации органических жидкостей, обладающих сложной структурой. В основе этого метода лежит закономерность, в соответствии с которой отношение изменения энтальпии и радиуса частицы при изменении температуры от Ti до T-i является константой, характерной для данной частицы.
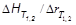 = Const =
= Const = 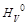
В табл. 32 приведены значения этих констант для ряда органических веществ.
Таблица 32
| Соединение | 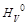
| Соединение | 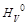
|
| н-Пентан | Бензол | ||
| н-Гексан | Толуол | ||
| н-Гептан | о-Ксилол | ||
| н-Октан | м-Ксилол | ||
| н-Нонан | п-Ксилол | ||
| н-Декан | Этилбензол | ||
| н-Ундекан | Кумол | ||
| н-До декан | Циклопентан | ||
| н-Тетрадекан | Циклогексан | ||
| н-Гексадекан | Метилциклопентан | ||
| 2,2,4-Триметилпентан | Метилциклогексан | ||
| Изобутилен | Нитробензол | ||
| СС11 | Метанол |
Методы анализа, основанные на взаимодействии с электромагнитным и корпускулярным излучением. В зависимости от участка электромагнитного спектра и форм внутренней энергии, определяющих принцип анализа, различают большую группу методов, объединенных под общим наименованием "спектроскопические методы анализа". Обзор этих методов представлен на рис. 142.
Физические величины, используемые в спектральных методах анализа, представлены в табл. 33. Спектры являются наиболее распространенным видом двумерной аналитической информации.При этом частоты или длины волн характеризуют химическую природу компонентов, а соответствующие интенсивности используются для определения концентрации этих компонентов.
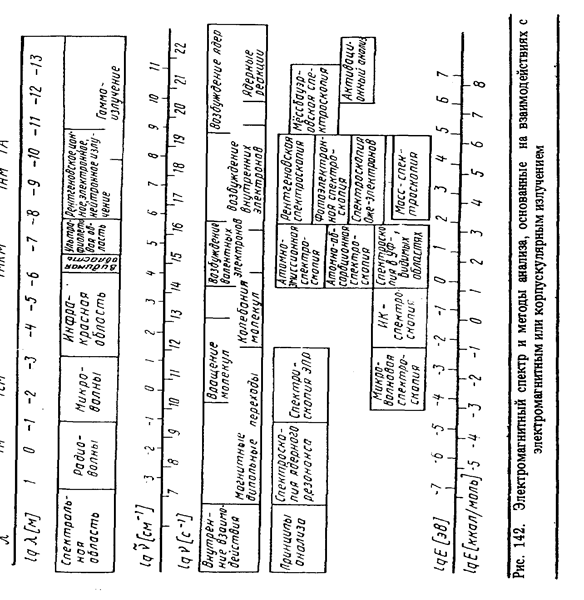
Таблица 33
| Измеряемая величина | Функциональная зависимость | Обозначение |
| Длина волны l | ||
Волновое число 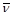
| 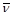 =1/l =1/l
| |
| Частота v | v=c/l | с - скорость света |
| Энергия излучения Е | E=hv=hc/l | h - постоянная Планка |
| Термическая энергия Е | Е =½ fkT | k — постоянная Больцмана / - число степеней свободы внутренней энергии |
| Кинетическая энергия Еk | Еk = ½ т 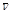 2 2
| т - масса частицы Г - средняя скорость части цы |
| Длина волны де Бройпя Л. | l = h/mv | |
| Интенсивность l |
Таким образом, даже краткий обзор основных видов взаимодействий, определяющих принципы химического анализа, показывает, что при проведении химического анализа используются измерения практически всех известных физических величин.
Это обстоятельство составляет одну из особенностей измерения концентрации и предопределяет связь данного вида измерений с другими, как это представлено на рис. 143.
Только этим, однако, не исчерпываются особенности измерений в химическом анализе. Определяющим для понимания специфики измерения концентрации, а тем самым для разработки методов метрологического обеспечения данного вида измерений, является место измерений в качественном и количественном анализе.
Дата добавления: 2015-02-05; просмотров: 1906;
