Измерение параметров периодических процессов

Критерии, приводящие к отношению правдоподобия. Обозначим через PN вероятность того, что сигнал на выходе оптимального фильтра представляет собой только реакцию на помеху, а через PX+N — вероятность того, что в нем содержится еще и отклик на полезный входной сигнал. Тогда вероятность ошибочного решения
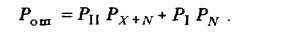
Естественно, что условный „идеальный наблюдатель", принимающий решения, либо вообще не должен совершать ошибок, либо должен свести до минимума их вероятность. Поэтому критерий
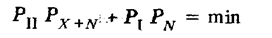
называется критерием идеального наблюдателя. Он является частным случаем критерия минимума среднего риска, в котором учитывается значимость или стоимость ошибок каждого вида:

Заменяя PIна 1 — P0 и выполняя преобразования, тот и другой критерии можно представить в общем виде:
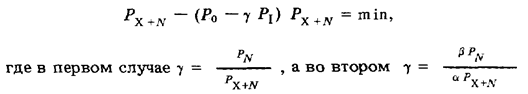
Последнее выражение минимизируется при
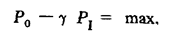
что вполне понятно, так как вероятность правильного обнаружения желательно иметь возможно большую, а вероятность ложной тревоги возможно меньшую.
Полученное выражение может рассматриваться самостоятельно и называется критерием взвешенной (с помощью g) комбинации (из двух слагаемых).
Для того, чтобы вывести из критерия взвешенной комбинации значение Wopt введем в рассмотрение функцию решения
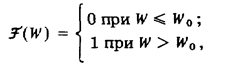
с помощью, которой выражения для вероятности правильного обнаружения и вероятности ложной тревоги запишутся в виде:
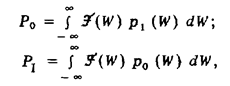
где значения интегралов на участке изменения переменной от — ∞ до неоптимального пока еще порога W0 равны нулю.
Критерий взвешенной комбинации можно тогда представить в виде
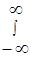 p0 (W) F(W) (L - g) dW = max,
p0 (W) F(W) (L - g) dW = max,
где L =  называется отношением правдоподобия.
называется отношением правдоподобия.
 В подынтегральном выражении с порогом обнаружения связана только функция решения. Следовательно, максимизировать интеграл можно только за счет выбора этой функции. Но она имеет всего два значения: 0 и 1. Поэтому поступим следующим образом. Принимая во внимание, что плотность распределения вероятностиp0 (W) всегда положительна, будем придавать функции решения F(W) значение 0, если разность L — g отрицательная, и значение 1, если эта разность положительная. В этом случае, очевидно , значение интеграла
В подынтегральном выражении с порогом обнаружения связана только функция решения. Следовательно, максимизировать интеграл можно только за счет выбора этой функции. Но она имеет всего два значения: 0 и 1. Поэтому поступим следующим образом. Принимая во внимание, что плотность распределения вероятностиp0 (W) всегда положительна, будем придавать функции решения F(W) значение 0, если разность L — g отрицательная, и значение 1, если эта разность положительная. В этом случае, очевидно , значение интеграла
будет максимальным, а оптимальное правило решения запишется в виде
ì0 при L£g
Fopt (W) í
î1 при L>g
Дальнейшее зависит от того, что представляет собой отношение правдоподобия. С одной стороны; как отношение двух плотностей вероятности оно не может быть отрицательным. С другой стороны; конкретный его вид зависит от законов распределения вероятности сигнала на выходе оптимального фильтра при наличии и при отсутствии в нем отклика на полезный входной сигнал. Таким образом, в отличие от синтеза оптимального порога обнаружения по критерию Неймана — Пирсона здесь требуется знание р1 (W) в реальных условиях эксплуатации. На практика обычно корректируют порог по мере накопления необходимых сведений, либо задаются моделью сигнала на этапе проекти- рования средства измерений.
Пример 48. Реакция оптимального фильтра на помеху подчиняется нормированному нормальному закону распределения вероятности, а отклик на полезный входной сигнал равен 1. Определить оптимальный порог обнаружения при заданном значении у.
Решение. Отношение правдоподобия
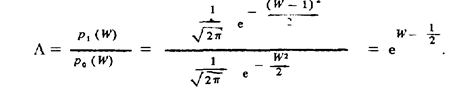
График этой функции построен на рис. 97, а. При L  g оптимальная функция решения Fopt (W) = 0, и принимается решение, что полезного сигнала нет. При L > g Оптимальная функция решения Fopt(W) = 1 принимается решение, что полезный сигнал есть (см. рис. 97, б) : Отсюда
g оптимальная функция решения Fopt (W) = 0, и принимается решение, что полезного сигнала нет. При L > g Оптимальная функция решения Fopt(W) = 1 принимается решение, что полезный сигнал есть (см. рис. 97, б) : Отсюда
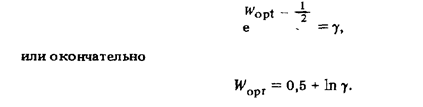
Теория статистических решений используется также при контроле.
* В примерах 24. . .28 предполагается, что остальными факторами, влияющими на результат измерения, можно пренебречь.
Измерение параметров периодических процессов
Измерение параметров может представлять как самостоятельный интерес, так и проводиться с целью последующего восстановления сигнала. В том и в другом случае параметры измеряются на выходе средства измерений, после чего могут пересчитываться на вход.
Периодическому входному сигналу соответствует и периодический отклик на него. Он может быть представлен дискретным спектром
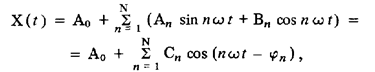
из чего следует, что параметрами, подлежащими измерению и позволяющими полностью восстановить как отклик Х(t), так и (после пересчета их на вход) входной сигнал Q (t) являются постоянная составляющая
A0 = 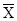 =
= 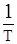
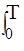 X(t) dt
X(t) dt

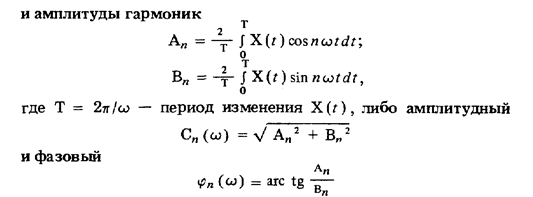
спектры отклика.
На практике большей частью интерес представляет амплитудный спектр. Для выделения его составляющих используются селективные фильтры с узкой полосой пропускания. Примерами таких фильтров являются резонансные системы с сосредоточенными или распределенными постоянными, RC-фильтры, электромеханические и пьезоэлектрические фильтры и т. п.
Составляющие спектра могут анализироваться одновременно, либо поочередно. Соответственно различают параллельный и последовательный спектральный анализ.
При параллельном спектральном анализе исследуемый сигнал подается одновременно на п селективных фильтров, на выходе каждого из которых измеряется амплитуда соответствующей составляющей амплитудного спектра (см. рис. 98). Резонансные характеристики фильтров должны охватывать весь диапазон возможных частот, так что 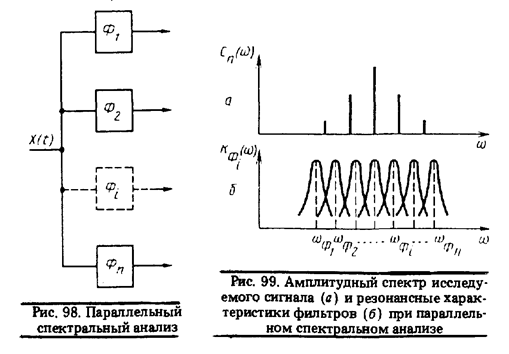 перекрывают друг друга (рис. 99). В результате отклик на каждую составляющую появляется на выходе не одного, а нескольких фильтров. Это усложняет анализ и снижает его точность. Кроме того, количество фильтров не может быть очень большим, что налагает ограничение на число анализируемых гармоник в спектре, а следовательно, опять-таки на точность спектрального анализа. Но главным недостатком является сложность многоканальных спектроанализаторов, возрастающая еще более при введении дополнительных функциональных узлов с целью автоматизации измерений и обработки экспериментальных данных.
перекрывают друг друга (рис. 99). В результате отклик на каждую составляющую появляется на выходе не одного, а нескольких фильтров. Это усложняет анализ и снижает его точность. Кроме того, количество фильтров не может быть очень большим, что налагает ограничение на число анализируемых гармоник в спектре, а следовательно, опять-таки на точность спектрального анализа. Но главным недостатком является сложность многоканальных спектроанализаторов, возрастающая еще более при введении дополнительных функциональных узлов с целью автоматизации измерений и обработки экспериментальных данных.
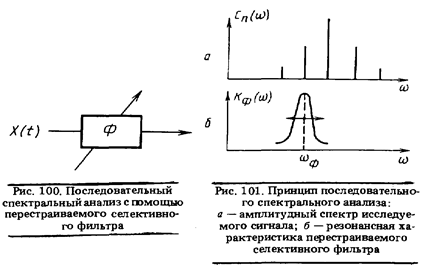
При последовательном спектральном анализе гармоники в спектре исследуемого сигнала анализируются поочередно путем перестройки селективного фильтра по частоте. Структурная схема такого анализатора спектра (см. рис. 100), принцип действия которого показан на рис. 101, могла бы быть очень простой, если бы перестройка фильтра в широком диапазоне частот не приводила к ухудшению его селективных свойств. Преодоление этого недостатка приводит к усложнению схемы, тем не менее последовательный анализ применяется гораздо чаще, чем параллельный.
Широкое применение находит измерение интегральных параметров выходного сигнала, перечисленных в предыдущем разделе (среднего, средневыпрямленного и среднего квадратического значения). При периодических процессах их большим достоинством является то, что при меняющемся во времени сигнале эти параметры в стационарном режиме работы средства измерений остаются постоянными, что позволяет градуировать шкалы приборов методами, рассмотренными в разд. 4.5.1. Благодаря наличии» связи между параметрами, достаточно измерить любой из ниx для того, чтобы найти все остальные, если только известна форма сигнала. Для этого существуют таблицы, подобные табл. 22.
Таблица 22
| Форма сигнала | ka | kф | kу |
| Гармоническая | 1,41 | 1,11 | 1,56 |
| Пилообразная | 1,73 | 1,16 | 2,00 |
| Меандр | 1,00 | 1,00 | 1,00 |
Замечание 1. Отечественная промышленность выпускает аналоговые вольтметры, измеряющие либо амплитудное (пиковое), либо средневыпрямленное, либо среднее квадратическое значение напряжения. Однако шкалы всех их градуированы в средних квадратических значениях синусоидального напряжения, так как исторически измерение переменных напряжений было начато в электротехнике, где интересуются в первую очередь энергетическим уровнем напряжения. Поэтомупри измерении синусоидального напряжения все вольтметры показывают среднее квадратическое значение. Исключение составляют импульсные вольтметры, шкалы которых градуированы в максимальных (пиковых) значениях.
Пример 50.При измерении синусоидального напряжения показание вольтметра, измеряющего средневыпрямленное значение, равно 100 В. Чему равны интегральные параметры напряжения?
Ответ: U ск = 100 В; U m = U ск · k a = 141 В; U св = U ск / kф= 90 В.
Замечание 2. При измерении несинусоидального напряжения для перехода от показания вольтметра к значению измеряемого им параметра используются коэффициенты, приведенные в первой строке табл. 22.
Пример 51.При измерении несинусоидального напряжения выполняются условия предыдущего примера. Чему равны интегральные параметры напряжения?
Ответ: U св = 100/1,11= 90 В. Остальные параметры определить невозможно, так как неизвестна форма напряжения и соответствующие ей коэффициенты k a и kф.
Пример 52.Выполняются условия предыдущего примера, но измерение выполнено вольтметром; среднего квадратического значения. Чему равны интегральные показатели напряжения?
Ответ: t/ск = 100 В, Остальные параметры определить невозможно.
Пример 53.Выполняются условия двух предыдущих примеров, но измерение выполнено пиковым вольтметром. Чему равны интегральные показатели напряжения?
Ответ: t/max =1,41 · 100 = 1в1 В. Остальные показатели определить невозможно.
Замечание 3. Если форма напряжения известна (т. е. известны соответствующие ей коэффициенты k a и kф), то переход от измеренного интегрального показателя к остальным осуществляется с помощью множителей, приведенных в табл. 23.
Таблица 23
| Вольтметр | U max Uмах | U ск | U св |
| Пиковый | 1,41 | 1,14/ k a | 1,41 / k у |
| Среднего квадратического значения | k a | 1/ k у | |
| Средневьшрямленного значения | 0,9 / k у | 0,9/ k ф | 0,9 |
| Импульсный | 1/ ka | 1/ k у |
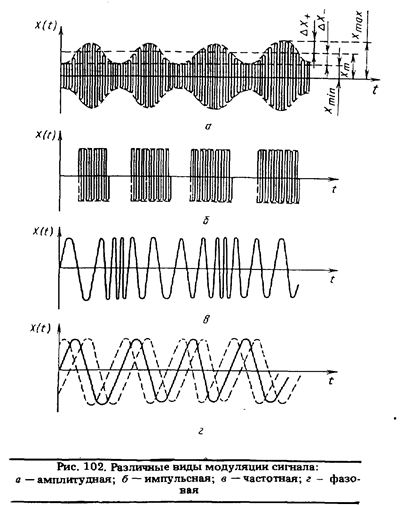
К периодическим процессам относятся многие виды модулированных сигналов. Наиболее распространенными являются показанные на рис. 102 амплитудная (и ее разновидность — импульсная), частотная и фазовая модуляции. Частота несущих колебаний обычно бывает известна, и интерес представляют только параметры модуляции, по которым сигнал может быть полностью восстановлен. Разумеется, все они определяются с помощью спектроанализатора, но для измерения некоторых существуют более простые методы. В качестве примеров рассмотрим измерение коэффициента амплитудной модуляции и девиации частоты.
Амплитудно-модулированный сигнал при периодической модулирующей функции может быть представлен в виде
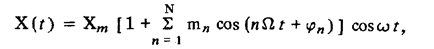
где Ω — частота первой гармоники модулирующего колебания, а коэффициент амплитудной модуляции mn= ХnΩ / Хm зависит от амплитуды п-й гармоники модулирующего колебания ХnΩ . Наибольший. интерес обычно представляет значение коэффициента амплитудной модуляции по первой гармонике m1 = ХΩ / Хm . Помимо него, измеряют среднее значение, численно равное (см. рис. 102).
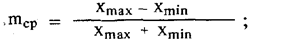
пиковые значения, определяемые как
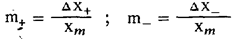
и измеряемые раздельно „вверх" (+) и вниз (—) . В общем случае
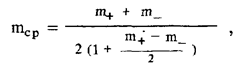
а при тональной амплитудной модуляции (N = 1)
m+ = m_ = m cp = m1 = m.
Легко видеть, что m cp и m+ , m_ определяются непосредственно по записи амплитудно-модулированного сигнала на ленте самописца или по осциллограмме. Если Х(t) — напряжение (преобразованный в напряжение сигнал), то после его детектирования постоянная составляющая, пропорциональная средневыпрямленному значению напряжения, измеряется магнитоэлектрическим вольтметром, а пиковое значение переменной составляющей — пиковым вольтметром с закрытым входом, переключая полярность которого, можно измерять ΔХ+ и ΔХ_. Если входным аттенюатором установить и поддерживать показание магнитоэлектрического вольтметра равным 1, то шкала пикового вольтметра может быть проградуирована прямо в значениях коэффициента модуляции. Поэтому магнитоэлектрический вольтметр заменяют схемой автоматической установки и стабилизации Хm = 1.
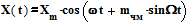 |
Частотно-модулированный по гармоническому закону сигнал записывается в виде:
где W — частота модуляции, а mчм = Dω/W-индекс модуляции, пропорциональный девиации частоты Dω. Девиация частоты является основным параметром, характеризующим частотно-модулированный сигнал. Для ее измерения чаще всего используется частотное детектирование. Частотно-модулированный сигнал преобразуется частотным детектором в низкочастотное напряжение, амплитуда переменной составляющей которого, измеряемая пиковым вольтметром, пропорциональна девиации частоты. Шкалу пикового вольтметра можно проградуировать прямо в единицах девиации частоты (обычно килогерцах).
Дата добавления: 2015-02-05; просмотров: 1171;
