Оптимальная фильтрация
Согласование динамических свойств средств измерений с характером входных воздействий важно и при измерениях по шкале порядка. К последним, как уже отмечалось, относятся измерения с помощью индикаторов, сравнивающих неизвестный размер измеряемой величины с нулевым.
Согласно математической модели измерения по шкале порядка (8), сравнение неизвестного размера Q1 с нулевым Q2 = 0 в условиях аддитивных случайных воздействий h, называемых помехами, сводится к решению вопроса: присутствует в левой части выражения (8) слагаемоеQ1 = Q (t), или оно равно нулю, и выражение (8) является тождеством h(t) º h(t) ?
Так как решение принимается на основе анализа выходного сигнала Х (t), то задача ставится так: присутствует в
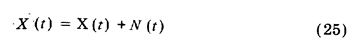
полезный сигнал X(Q) являющийся откликом на Q (t), или выходной сигнал является результатом воздействия на средство измерений аддитивных помех случайного характера N (t) ? Эта задача называетсязадачей обнаружения полезного сигнала на фоне аддитивных помех.
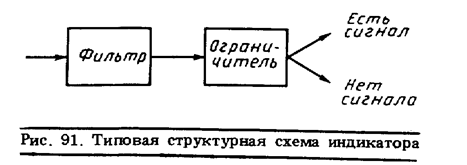
Средство измерений, решающее задачу обнаружения, с одной стороны, должно максимально способствовать тому, чтобы полезный сигнал, если он есть, как можно четче проявился бы на выходе; с другой стороны, решение о его наличии или отсутствии должно приниматься с достаточной степенью уверенности. Соответственно структурные схемы индикаторов включают обычно из: фильтр, предназначенный для выделения полезного сигнала, и ограничитель, реализующий решающее правило — рис. 91.
Для того, чтобы определить каким должен быть селективный фильтр, зададимся моделью помехи. Будем считать, что помеха представляет собой нормальный случайный процесс со средним значением, равным нулю, и равномерным энергетическим спектром Gh(w) = G0 = const. Такая модель помехи называется бельм шумом и соответствует, например, наличию на входе фильтра тепловых шумов.
Пусть на вход фильтра кроме помехи воздействует полезный сигнал (t), комплексный спектр которого Q(w). Спектр отклика на полезный сигнал и энергетический спектр помехи на выходе фильтры равны соответственно
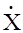 (w) =
(w) = 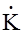 (w)
(w) 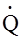 (w)
(w)
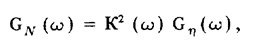
где К(w) — модуль комплексного коэффициента преобразования фильтра К(w) . Мощность отклика на полезный сигнал на выходе фильтра

а эффективная мощность помехи, равная ее дисперсии,
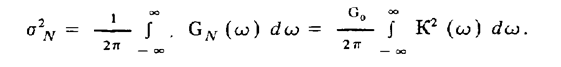
Фильтр наилучшим образом решит задачу выделения полезного сигнала, если в какой-нибудь момент времени t0 максимизирует отношение пиковой мощности сигнала к эффективной мощности помехи:

Синтезированный по этому критерию фильтр называется оптимальным. Для определения его основной метрологической характеристики — комплексного коэффициента преобразования — воспользуемся неравенством Буняковского-Шварца:

причем неравенство переходит в равенство, т. е. отношение пиковой мощности сигнала на выходе фильтра к эффективной мощности помехи максимизируется, если

где Q(w) — комплексно сопряженный спектр входного сигнала.
Полученный результат говорит о том, чтодинамическая характеристика оптимального фильтра должна быть согласована с входным воздействием. В частности, амплитудно-частотная и фазочастотные характеристики оптимального фильтра
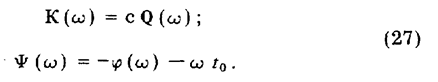
Справедливо и обратное: любой фильтр оптимален только для одного вида сигналов, имеющих соответствующий спектр.
Пример 45. Построить графики АЧХ и ФЧХ фильтра, оптимального для обнаружения прямоугольного импульса длительностью tи.
Решение. 1. Спектр прямоугольного импульса показан на рис. 92, а. Амплитудный и фазовый спектры представлены, соответственно, на рис. 92, б и в.
АЧХ оптимального фильтра, согласно первой из формул (27), может отличаться от амплитудного спектра входного сигнала только масштабом. Она построена на рис. 92, г.
ФЧХ, соответствующая второй формуле (27), построена на рис. 92, д.
Сравнивая результат, полученный в примере 45, с представленным на рис. 84, можно заключить, что оптимальный фильтр искажает форму входного сигнала. Это накладывает ограничения на области применения оптимальных фильтров. Они предназначены не для измерения меняющихся во времени физических величин по шкале отношений, а для обнаружения слабых сигналов на фоне соизмеримых с ними помех. Оптимальная фильтрация позволяет улучшить отношение сигнал/шум на выходе фильтра по сравнению со входом.

Происходит это за счет двух причин. Во-первых, фазочастотная характеристика оптимального фильтра такова, что в момент t0 все гармоники полезного сигнала на выходе складываются в фазе. В этом легко убедиться, подставив в выражение для фазы любой гармоники в момент времени t0

значение Y(w) из второй формулы (27). В результате в момент времени t0 происходит выброс сигнала; он достигает своего пикового значения. Во-вторых, амплитудно-частотная характеристика оптимального фильтра такова, что подавление основных энергонесущих составляющих полезного сигнала происходит незначительно, в то время, как энергия помехи ослабляется существенно. В результате отношение сигнал / помеха, пропорциональное отношению заштрихованных площадей на рис. 93, заметно отличается на входе и выходе оптимального фильтра. Выигрыш получается тем более значительным, чем сложнее входной сигнал. В этом нетрудно убедиться, рассмотрев АЧХ фильтра, оптимального последовательности прямоугольных импульсов. Как видно из рис. 94, оптимальный фильтр, получивший название гребенчатого, отфильтровывает индивидуально каждую гармонику полезного сигнала. Энергия помехи в промежутках между резонансными частотами подавляется.
 Зная динамическую характеристику оптимального фильтра, можно составить его функциональную схему.
Зная динамическую характеристику оптимального фильтра, можно составить его функциональную схему.
Дата добавления: 2015-02-05; просмотров: 1939;
