Статические и динамические измерения
Рассмотренные выше режимы работы средств измерений приведены на рис. 83. Измерения постоянных величин в установившемся режиме, а также измерения в стационарном режиме параметров протекающих во времени процессов относятся к статическим. Измерения постоянных величин в переходном режиме, меняющихся во времени величин в стационарном режиме, а также любые измерения в нестационарном режиме, как самих величин, так и параметров протекающих во времени процессов относятся к динамическим.
 При статических измерениях имеется возможность воспользоваться градуировкой шкалы отчетного устройства по известным входным воздействиям (значениям самой измеряемой величины, либо значениям параметров протекающих во времени процессов). Связь между входным воздействием и откликом на него устанавливается функцией преобразования
При статических измерениях имеется возможность воспользоваться градуировкой шкалы отчетного устройства по известным входным воздействиям (значениям самой измеряемой величины, либо значениям параметров протекающих во времени процессов). Связь между входным воздействием и откликом на него устанавливается функцией преобразования
средств измерений (см. разд. 4.5.1).
При динамических измерениях существенную роль могут играть инерционные свойства средства измерений. Они учитываются его динамическими характеристиками, которые могут быть полными и частными.
Полные динамические характеристики исчерпывающим образом описывают инерционные свойства средства измерений.К ним относятся:
уравнение динамики;
передаточная функция;
комплексный коэффициент преобразования (совокупность амплитудно-частотной и фазочастотной характеристик);
переходная характеристика;
импульсная характеристика.
Частные динамические характеристики отражают лишь некоторые инерционные свойства средств измерений. Это отдельные параметры полных динамических характеристик или некоторые величины, определяющие динамику протекания процессов: время установления показаний, ширина полосы пропускания частот и др.
На динамические характеристики средств измерений (полные и частные) устанавливаются нормы. Соответствие динамических характеристик этим нормам проверяется при поверке средств измерений. С этой целью в качестве входных воздействий используются так называемые испытательные сигналы, теоретические модели которых представлены в табл. 19.
Наиболее распространенными испытательными сигналами являются:
единичная ступень;
единичный импульс;
монохроматическое колебание.
Переходная характеристика экспериментально определяется как отклик средства измерений на входное воздействие в виде единичной ступени.
Импульсная характеристика определяется экспериментально как отклик средства измерений на входное воздействие в виде единичного импульса.
Как уже отмечалось,единичный импульс является первой производной от единичной ступени.У линейных средств измерений соотношение между откликами остается таким же, как между входными воздействиями. Поэтому
g(t) =h'(t) .
Подставляя в формулу (18) изображение единичного импульса Q(p) = d(p) = 1 (см. табл. 19), нетрудно убедиться в том, чтопередаточная функция является изображением отклика средства измерение на единичный импульс:
 W (p) =
W (p) = 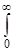 g(t) e-pt dt (21)
g(t) e-pt dt (21) 
На этом основывается экспериментальный способ опрeделения передаточной функции. Кроме того, она может быть вычислена теоретически путем решения уравнения динамики операторным методом (см. пример 39).
Спектр единичного импульса d(w) = 1. Подставляя это значение в формулу (20) убеждаемся, чтокомплексный коэффициент преобразования является спектром отклика средства измерений на единичный импульс:
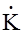 (w) =
(w) =  g(t) e-jwt dt .(22)
g(t) e-jwt dt .(22)
Амплитудно-частотную K(w) и фазочастотную j(w) характеристики можно построить по точкам, подавая на вход средства измерений монохроматические колебания разных частот и регистрируя изменение амплитуды и фазовую задержку отклика в стационарном режиме.
 Сравнивая выражения (21) и (22), легко заметить их тождественность при р = j w , так как g (t) =0 при t < О. Отсюда
Сравнивая выражения (21) и (22), легко заметить их тождественность при р = j w , так как g (t) =0 при t < О. Отсюда
W(jw) = K(w) .
Взаимосвязь между различными динамическими характеристиками представлена табл. 21.
  Известны
Опре
деляются Известны
Опре
деляются
| h(t) | g(t) | W(p) |
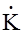 (w) (w)
|
| h(t) |
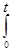 g(t) dt g(t) dt
|
L-1[ 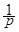 W(p)] W(p)]
|
Ф-1[ 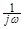 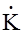 (w)] (w)]
| |
| g(t) | h’(t) | L-1[W(p)] |
Ф-1[ 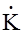 (w)] (w)]
| |
| W(p) | L[h’( t )] | L[g(t)] |
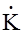 (jp) (jp)
| |
| K(w) | Ф[h’ (t) ] | Ф[g(t)] | W(jw) |
При экспериментальном определении динамических характеристик приходится считаться с тем, что реальные испытательные сигналы несколько отличаются от их теоретических моделей. Возможно, более точное воспроизведение испытательных сигналов составляет главную проблему метрологического обеспечения динамических измерений.
Важную роль при динамических измерениях играют искажения отклика по сравнению с входным воздействием. Под искажениями понимаются любые изменения формы входного воздействия. Изменение масштаба, а также задержка отклика на время t по сравнению с входным воздействием не относятся к искажениям. Поэтомуусловие преобразования средством измерений входного воздействия без искажений можно записать следующим образом:
X (t) = Ko Q( t -t) ,
 где Ко = const. В операторной форме, согласно табл. 19, X(p) = K0 Q(p) e-rt
где Ко = const. В операторной форме, согласно табл. 19, X(p) = K0 Q(p) e-rt
откуда следует, что средством измерений будет осуществляться преобразование входного воздействия без искажений, если его передаточная функция
W (p) = K0 e-rt(23)
Положив р = jw , можно получить условие преобразования входного воздействия без искажений в другом виде:

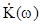 = K0 e-jwt (24)
= K0 e-jwt (24)
Амплитудно-частотная и фазочастотная характеристики средства измерений, преобразующего входное воздействие без искажений, показаны на рис. 84.
Условия безыскаженного преобразования (23) и (24) справедливы при любом входном воздействии. Соблюдаются они только при отсутствии в средствах измерений реактивных элементов, когда К0 = const, а t = 0. На практике для безыскаженного преобразования достаточно чтобы АЧХ была равномерной, а ФЧХ линейной в полосе частот, занимаемой спектром входного воздействия.
Пример 44. На измерительный преобразователь с идеализированными АЧХ и ФЧХ, показанными на рис. 85 (фильтр нижних частот), подается входное воздействие в форме прямоугольного импульса с высотой U0 и длительностью tu. Исследовать зависимость искажений отклика от ширины полосы пропускания частот измерительного преобразователя.
Решение. 1. Представим прямоугольный импульс в виде двух скачков напряжения так, как это показано на рис. 86:

Дата добавления: 2015-02-05; просмотров: 2565;
