Статистические решения
После оптимального фильтра выходной сигнал W (t) в индикаторах поступает на ограничитель (см. рис. 91), представляющий собой пороговое устройство. В случае превышения им порога обнаружения W 0 принимается решение, что в нем содержится полезный сигнал X(t), являющийся откликом на входное воздействие Q (t). В противном случае считается, что W (t) является реакцией оптимального фильтра на помеху h (t) . В соответствии с основным постулатом метрологии результат измерения (а при измерениях по шкале порядка результатом измерения служит решение) является случайным. Возникает вопрос, какова вероятность правильного и неправильного решения?
Ответ на этот вопрос дает теория статистических решений.
Рассмотрим графическую интерпретацию ситуаций, которые возникают в процессе принятия решения.
На рис. 96 построены графики плотности распределения вероятности сигнала на выходе оптимального фильтра при
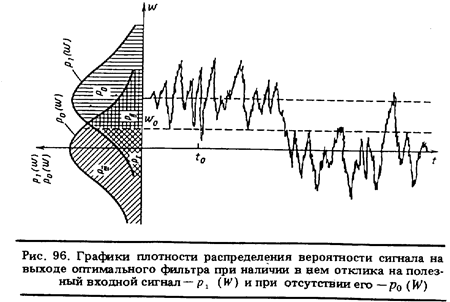
наличии в нем отклика на полезный входной сигнал — p1 (W) и при его отсутствии – р0(W). В случае превышения сигналом W(t0) порогового значения W 0 считается, что он подчиняется закону распределения вероятности с плотностью p1(W). Вероятность р0 того, что такой сигнал окажется в интервале значений [W 0 ; ∞] , равна (см. разд. 2.2) :

Она называется вероятностью правильного обнаружения. На рис. 96 площадь, равная вероятности правильного обнаружения, заштрихована штриховкой, перпендикулярной оси W. Может однако случиться, что. в момент времени t0 сигнал на выходе оптимального фильтра, содержащий отклик на полезный входной сигнал, примет значение, меньшее W0. Тогда будет принято неправильное решение о том, что "полезного сигнала на входе оптимального фильтра нет. Вероятность такого неправильного решения, называемая вероятностью ошибки второго рода (см. разд. 2.6.2),
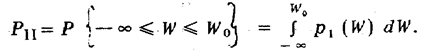
На рис. 96 площадь, равная вероятности ошибки второго рода, заштрихована двойной косой штриховкой.
Если в сигнале на выходе оптимального фильтра нет отклика на полезный входной сигнал, то он подчиняется закону распределения вероятности с плотностью р0 (W). В случае превышения таким сигналом в момент времени t0 порогового значения W 0 будет принято ошибочное решение о том, что полезный сигнал на входе оптимального фильтра есть. Вероятность такой ошибки первого рода

На рис. 96 площадь, равная вероятности ошибки первого рода, заштрихована штриховкой, параллельной оси W. Вероятность правильного решения о том, что полезного сигнала на входе оптимального фильтра нет, принимаемого при W (t0) < W 0 ,
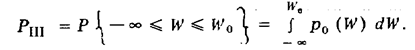
Соответствующая площадь на рис.96 заштрихована косой штриховкой.
При всех обстоятельствах

Анализ рассмотренных ситуаций показывает, что при уменьшении порога обнаружения W0 увеличивается вероятность правильного обнаружения Р0 и уменьшается вероятность ошибки второго рода РII, но одновременно растет вероятность ошибки первого рода PI и уменьшается вероятность правильного решения об отсутствии полезного сигнала РIII . При увеличении порога обнаружения W0, наоборот, вероятность правильного решения об отсутствии полезного сигнала РIII увеличивается, а вероятность ошибки первого рода PI уменьшается, но растет вероятность ошибки второго рода РIIи уменьшается вероятность правильного обнаружения Р0 . При столь противоречивых тенденциях выбор оптимального значения порога обнаружения WНПдолжен производиться на основе какого-либо критерия.
Критерий Неймана — Пирсона. Простейшим критерием является требование обеспечить заданную вероятность ошибки первого рода (иногда ее называют вероятностью ложной тревоги). Согласно этому критерию, называемому критерием Неймана —Пирсона, значение порога обнаружения WНПопределяется из уравнения
 PI =
PI = 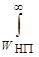 p0 (W) dW ,
p0 (W) dW ,
где вероятность ошибки первого рода PI является заданной. Критерий Неймана — Пирсона широко применяется на этапе проектирования средств измерений, так как не требует знания p1 (W) в реальных условиях эксплуатации.
Пример 47. Реакция оптимального фильтра на помеху подчиняется нормированному нормальному закону распределения вероятности. Установить значение порога обнаружения по критерию Неймана — Пирсона при заданной вероятности ложной тревоги РI = 0,1.
Дата добавления: 2015-02-05; просмотров: 1644;
