Основы ТЕОРИИ ИЗМЕРЕНИЙ
2.1. ОСНОВНОЙ ПОСТУЛАТ МЕТРОЛОГИИ
Любое измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражение первого через второй в кратном или дольном отношении. При измерении физических величин в качестве известного размера естественно выбрать единицу СИ. Тогда процедура сравнения неизвестного значения с известным и выражения первого через второе в кратном или дольном отношении запишется следующим образом: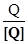 
. В квалиметрии сравнение производится обычно со значением базового показателя качества или с представлением о наивысшем качестве, которое оценивается максимальным количеством баллов.
На практике непосредственно неизвестный размер не всегда может быть представлен для сравнения с единицей. Жидкости, например, и сыпучие вещества представляются на взвешивание в таре. Очень маленькие линейные размеры могут быть измерены только после увеличения их микроскопом или другим прибором. В первом случае процедура сравнения выглядит как определение отношения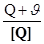 
во втором - 
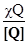, где в рассматриваемых примерах u - масса тары, а c- коэффициент увеличения. Само сравнение в свою очередь происходит под влиянием множества случайных и неслучайных, аддитивных (от латинского additives - прибавляемых) и мультипликативных (от латинского multiplico- умножаю) факторов, точный учет которых нeвoзмoжeн, а результат совместного воздействия непредсказуем. Ограничиваясь для простоты аддитивными воздействиями, совместное влияние которых можно учесть случайным слагаемым ŋ получим следующее уравнение измерения по шкале отношений:
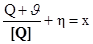
Оно выражает некоторое действие, процедуру сравнения в реальных условиях, которая, собственно, и является измерением. Главной особенностью измерительной процедуры является то, что при ее повторении из-за случайного характера η отсчет по шкале отношений х получается все время разным. Это фундаментальное положение является законом природы. На основании громадного опыта практических измерений, накопленного к настоящему времени, может быть сформулировано следующее утверждение, называемое основным постулатом метрологии:отсчет является случайнымчислом. На этом постулате, который легко поддается проверке и остается справедливым в любых областях и видах измерений, основана вся метрология.
Уравнение (2) является математической моделью измерения по шкале отношений. Отсчет в ней не может быть представлен одним числом. Его можно лишь описать словами или математическими символами, представить массивом экспериментальных данных, таблично, графически, аналитическим выражением и т.п. Проиллюстрируем это двумя примерами.
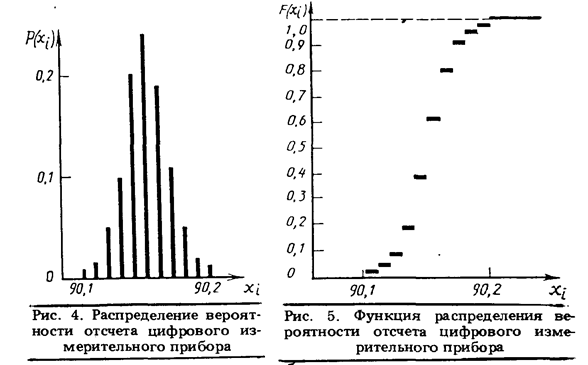
Пример 3. При п — кратном независимом измерении одной и той же физической величины постоянного размера на световом табло цифрового измерительного прибора в случайном порядке появлялись числа хi, представленные в первой графе табл. 5. Каждое i-е число появилось m, раз. Что представляет собой отсчет при таком измерении?
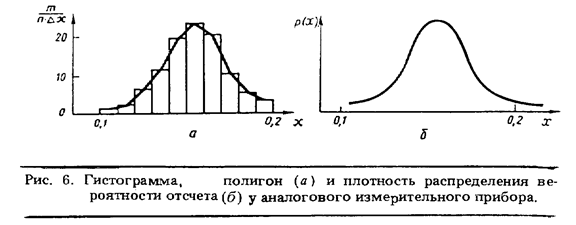
Решение. Ни одно из чисел в первой графе таблицы, взятое в отдельности, не является отсчетом. Отсчет характеризуется всей совокупностью этих чисел с учетом того, как часто они появлялись. Принимая частость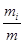 
каждого i-го числа за вероятность его появления Р(хi), заполним третью графу в табл. 5. В совокупности с первой она даст янм распределение вероятности отсчета, представленное таблично. Его же можно представить графически так, как это показано на рис. 4. А можно поступить и по другому. Проставим в четвертой графе табл. 5 вероятности того, что на табло показывающего измерительного прибора появится число, меньшее или равное тому, которое значится в первой графе. В совокупности с первой графой это даст нам представленную таблично функцию распределения вероятности отсчета. Графически она выглядит так, как это показано на рис. 5.
Таблица 5
| xi | m, | Р (хi) | F (хi) |
| 90,10 |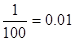 
| 0,01 | |
| 90,11 |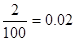 
| 0,01 +0,02 = 0,03 | |
| 90,12 |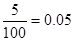 
| 0,03 + 0,05 = 0,08 | |
| 90,13 |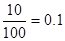 
| 0,08 + 0,1 = 0,18 | |
| 90,14 |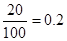 
| 0,18+0,2 = 0,38 | |
| 90,15 |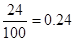 
| 0,38 + 0,24 = 0,62 | |
| 90,16 |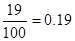 
| 0,62+0,19 = 0,81 | |
| 90,17 |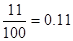 
| 0,81 + 0,11 = 0,92 | |
| 90,18 |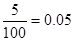
| 0,92 + 0,05 = 0,97 | |
| 90,19 |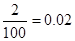 
| 0,97 + 0,02 = 0,99 | |
| 90,20 |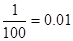 
| 0,99 + 0,01 = 1,00 |
Как распределение вероятности Р(хi), так и функция распределения вероятности F (хi)являются исчерпывающим описанием отсчета у цифровых измерительных приборов любой конструкции.
Пример 4. При n-кратном независимом измерении одной и той же физической величины постоянного размера аналоговым измерительным прибором указатель отсчетного устройства в случайной последовательности по m раз останавливался на каждом из делений шкалы:
| Деление шкалы | m |
| 0,10… 0,11 | |
| 0,11 … 0,12 | |
| 0,12… 0,13 | |
| 0,13… 0,14 | |
| 0,14 … 0,15 | |
| 0,15 … 0,16 | |
| 0,16 . . . 0,17 | |
| 0,17 . . . 0,18 | |
| 0,18 . . . 0,19 | |
| 0,19 . . . 0,20 |
Что представляетсобой отсчет при таком измерении?
 |
Решение. Принимая деления шкалы за основания, построим на них m прямоугольники с высотами, равными отношению частостей
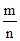к цене деления шкалы Dх (в данном случае безразмерной). Получившаяся фигура, показанная на рис. 6, а, называется гистограммой. Соединив теперь отрезками прямых середины верхних сторон прямоугольников, как это показано на рисунке, получим ломаную линию, называемую полигоном.
Как гистограмма, так и полигон являются исчерпывающим эмпирическим описанием отсчета у аналоговых измерительных приборов любой конструкции.
Если бы была возможность увеличивать п, то в пределе при п ® ∞ и Dx®0 полигон перешел бы в кривую плотности распределения вероятности отсчета р (хi), показанную на рис. 6, б.
 |
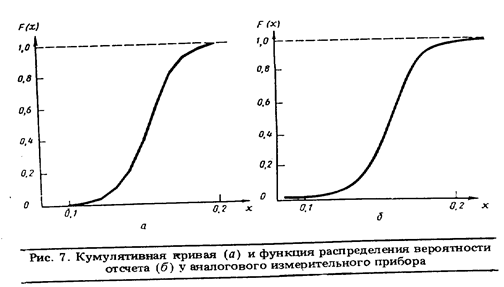Здесь так же, как в примере 3, можно поступить по-другому. Подсчитывая, сколько раз указатель отсчетного устройства останавливался левее каждой отметки шкалы, откладывая над этой отметкой вдоль оси ординат отношение числа таких отклонений к их общему числу n и соединяя полученные точки отрезками прямых, мы получим ломаную линию, показанную на рис. 7,а и называемую кумулятивной кривой. Как гистограмма и полигон, она исчерпывающе характеризует отсчет у аналоговых измерительных приборов. Если бы опять-таки была возможность увеличивать п, то при п ® ∞ и Dx®0 кумулятивная кривая перешла бы в график функции распределения вероятности отсчета .F(xi), показанный на рис. 7, б.
Плотность распределения вероятности р(х) и функция распределения вероятности F (х) служат в теории вероятности моделями эмпирических законов распределения, получаемых из экспериментальных данных методами математической статистики.
После выполнения измерительной процедуры в уравнении (2) остаются два неизвестных; Q и h. Неслучайное значение ύ либо должно быть известно до измерения, либо устанавливается посредством дополнительных исследований. Слагаемое h, являющееся случайным, не может быть известно в принципе. Поэтому определить значение измеряемой величины
Q =х [Q] -h [Q] - ύ (3)
Дата добавления: 2015-02-05; просмотров: 1135;