Невозможно.
Равенство (3) соблюдается точно, благодаря тому, что при повторных выполнениях измерительной процедуры случайное изменение второго слагаемого в правой части всякий раз влечет за собой точно такое же изменение первого. О таких слагаемых говорят, что они коррелированы (взаимосвязаны) между собой. Разность между коррелированными значениями двух случайных величин неслучайна, но в данном случае неизвестна. Поэтому строгого решения уравнение (3) не имеет.
На практике удовлетворяются приближенным решением. Для этого используются результаты специального исследования, называемого метрологической аттестацией средства измерений и методики выполнения измерений. В ходе этого исследования приближенно определяетсясреднее значение второго слагаемого в правой части формулы (3) :
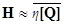
Среднее значение не является случайным. Поэтому после замены случайного второго слагаемого в правой части уравнения (3) неслучайным значением Н, получается приближенное решение
Q»x [Q] -Н- ύ (4)
в котором результат измерения Q является случайным значением измеряемой величины.
Первое слагаемое в правой части выражения (4) называется показанием
Х=х [Q].
Оно подчиняется тому же закону распределения вероятности, что и отсчет, но отличается от последнего тем, что
dimX =dimQ.
Два последних слагаемых в правой части формулы (4) представляют суммарную поправку
Θ = - Н- ύ,
которая может включать и большее количество составляющих в зависимости от числа учитываемых факторов*. Поправка не является случайной, но может изменяться от измерения к измерению по определенному закону. Поэтому в каждое отдельное значение показания Xi, может вноситься своя поправка Θi ,.
Результат измерения Q подчиняется тому же закону распределения вероятности, что показание и отсчет, но смещенному по оси абсцисс на значение суммарной поправки. Отдельное его значение
Qi = Xi + Θi (5)
получаемое всякий раз после выполнения измерительной процедуры, называется результатом однократного измерения. Среднее арифметическое значение результата измерения, полученное при многократном независимом измерении одной и той же величины постоянного размера.
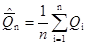 (6)
(6)
называется результатом многократного измерения.
Уравнение измерения интервала записывается аналогично уравнению (2):
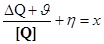 (7)
(7)
где DQ — значение разности между двумя размерами физической величины. Анализ этого уравнения не отличается от анализа уравнения (2).
Математической моделью измерения по шкале порядка служит неравенство
Q1 +h1 >< Q2+h2 (8)
описывающее процедуру сравнения двух размеров одной и той же измеряемой величины. Результатом сравнения в этом случае является не отсчет, а решение о том, какой из размеров больше, либо они одинаковы. Не исключена возможность как правильных, так и неправильных решений. Следовательно,результат сравнения двух размеров по шкале порядка является случайным, что соответствует основному постулату метрологии.
Измерения по шкале порядка широко применяются при контроле, когда в условиях случайных возмущений проверяемый размер Q1 сравнивается с контрольным (пороговым) Q2. Особое место занимает сравнение с Q2= 0, относящееся к теории обнаружения.
2.2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Математический аппарат теории вероятности широко используется в метрологии. Рассмотрим поэтому некоторые свойства законов распределения вероятности, являющихся моделями эмпирических законов распределения, получаемых из экспериментальных данных мсшдами математической статистики.
1. Прежде всего отметим, что функция F (х) определяет вероятность того, что отдельный результат, полученный по формуле (2) или (7), будет меньше ее аргумента.
2. Так как вероятность не может быть отрицательной, то
F (х) ³ 0.
Чем больше х, тем больше вероятность того, что ни один результат, полученный по формуле (2) или (7), не превысит этого значения, т.е. F (х) — неубывающая функция:
F (х2) ³ F (х 1), если х2 > х 1.
При изменении х от — ¥ до + ¥ F(x) меняется от 0 до 1.
3. Результат, полученный по формуле (2) или (7), меньше некоторого x1 с вероятностью F(х1) и меньше другого x2 > x1 с вероятностью F (х1). Следовательно, вероятность того, что результат сравнения по формуле (2) или (7) окажется в интервале [х1; х 2] , равна разности значений F(x) на границах этого интервала:
Р{x1£ х £ x2} =F (х2) -F (x1).
У аналогового измерительного прибора х1 и х2 можно выбирать сколь угодно близкими друг к другу. При x1 ® x2 F (x2) — F (x1) ® 0. Поэтому у аналоговых измерительных приборов вероятность того, что указатель отсчетного устройства остановится на какой-либо конкретной точке шкалы, равна 0. Отсюда следует, что
Р{х1 £ x £х2}= P{x1 <х £ х2}= P{x1 £ х <х2} =P{x1 < х <х2},
т.е. крайние точки можно включать, а можно и не включать в интервал.
4. Плотность распределения вероятности р (х) связана с функцией распределения вероятности F (х) соотношением
р (х) =F' (х).
Поэтому P (х) называют иногда дифференциальной функцией распределения вероятности.
В свою очередь F (х) может быть получена интегрированием р (х) в соответствующих пределах:
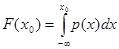
Геометрическая интерпретация этой операции показана на рис. 8, а F (x0) иногда называют интегральной функцией распределения вероятности.
5. Так как F (x) неубывающая функция, то ее производная не может быть отрицательной:
р (x) ³ 0.
|
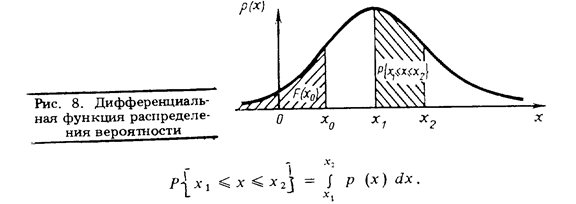 |
6. Вероятность того, что отдельный результат, полученный по формуле (2) или (7), окажется в интервале [x1;x2] , равна площади, ограниченной графиком функции р(х), осью абсцисс н перпендикулярами к ней на границах интервала (см.рис. 8):
7. При расширении интервала до бесконечности рассматриваемое событие становится достоверным. Поэтому площадь, ограниченная графиком функции р (х) и осью абсцисс, равна 1:

Описание отсчета или результата измерения с помощью законов распределения вероятности является наиболее поным, но неудобным. Во многих случаях ограничиваются приближенным описанием закона распределения вероятности с помощью его числовых характеристик, или моментов. Все они представляют собой некоторые средние значения, причем, если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра закона распределения — центральными.
Общее правило образования начальных моментов:
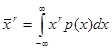
где r — номер момента.Важнейшим начальным моментом является первый— среднее значение
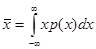
характеризующее математическое ожидание отсчета при бесконечном повторении процедуры измерения по формуле (2) или (7). Иногда математическое ожидание удобнее обозначать символом М (х). Свойства математического ожидания:
1) математическое ожидание неслучайного числа равно самому этому числу:
М(а) =а,
2) постоянный множитель можно выносить за знак математического ожидания:
М(aх) = аМ (х) , где а = const.;
3) математическое ожидание алгебраической суммы случайных чисел равно алгебраической сумме их математических ожиданий:
М(х +у - z) = М(х) +М(у) —M(z);
4) математическое ожидание произведения независимых случайных чисел равно произведению их математических ожиданий:
M(x∙y∙z) =M(x) M(y) M(z);
5) математическое ожидание отклонения случайного числа от его математического ожидания равно нулю:
М[х - М(х)] = 0.
Мерой рассеяния отдельных результатов, полученных по формуле (2) или (7), около их среднего значения служит второй центральный момент. Общее правило образования центральных моментов записывается следующим образом:
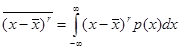
откуда сразу видно, что первый центральный момент тождественно равен нулю:
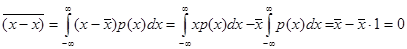
Второй центральный момент называется дисперсией и обозначается 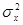 :
:
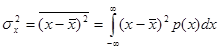
Иногда дисперсию удобнее обозначать символом D (х). Свойства дисперсии:
1) дисперсия неслучайного числа равна нулю:
D (а) = 0;
2) постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:
D (ах) = а2 D (х) , где а = const;
3) дисперсия алгебраической суммы двух случайных чисел
D(x ±y)=D(x)+ D(y) ± 2p 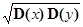 ,
,
где коэффициент корреляции
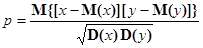
4) дисперсия алгебраической суммы независимых случайных чисел равна арифметической сумме их дисперсий:
D (х + у - z) = D (х) + D (у) + D (z );
5) дисперсия случайного числа равна разности между математическим ожиданием его квадрата-и квадратом математического ожидания:
D(x)= М(х2) -М2 (х).
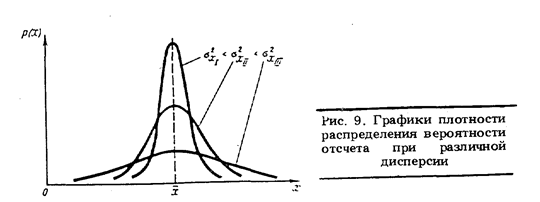
Чем больше дисперсия, тем значительнее рассеяние результатов, полученных по формулам (2), (7) относительно x. Это наглядно видно на рис. 9, где представлены кривые плотности одного и того же закона распределения вероятности отсчета при различных дисперсиях.
В метрологии в качестве меры рассеяния чаще используют среднее квадратическое отклонение
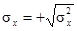
 |
Находит применение итретий центральный момент
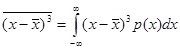
Мерой несимметричности распределения вероятности служит асимметрия
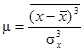
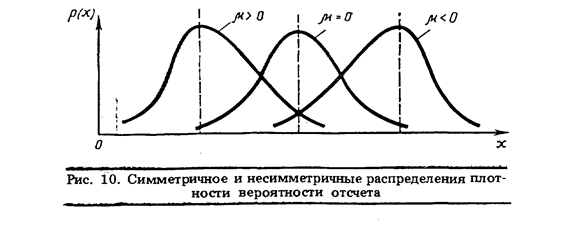 |
которая может быть положительной и отрицательной. Для симметричных распределений вероятности отсчета асимметрия равна нулю. На рис. 10 в качестве иллюстрации приведены примеры симметричного и несимметричных законов распределения вероятности с разными математическими ожиданиями.
Четвертый центральный момент используется для оценки заостренности дифференциальной функции распределения вероятности. Мерой заостренности служит эксцесс
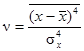
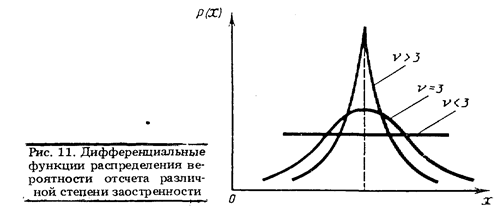 |
равный трем у закона распределения вероятности отсчета, кривая плотности вероятности которого имеет колоколообразную форму. Кривые с более острой вершиной имеют больший эксцесс, с более пологой — меньший, вплоть до отрицательного (рис.11).
Мерой неопределенности случайного числа является энтропия
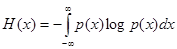
среднее значение логарифма плотности вероятности, взятое со знаком минус. Так как р(х)<1, то энтропия всегда положительна. Она равна нулю у неслучайного числа и максимальна при равномерной плотности распределения вероятности.
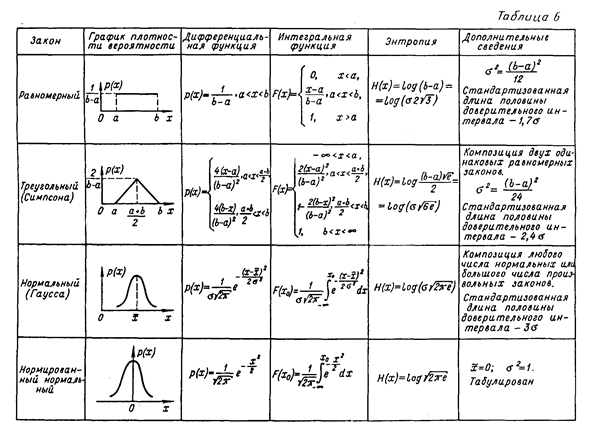
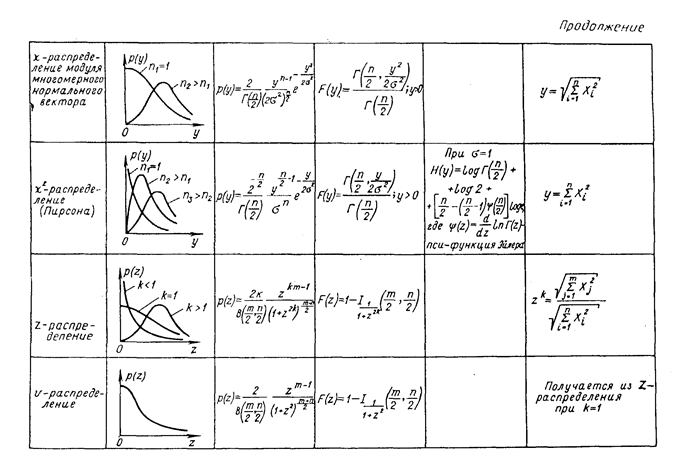
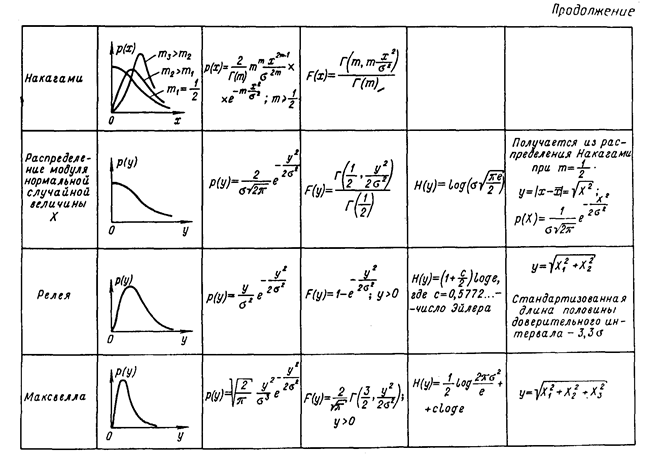
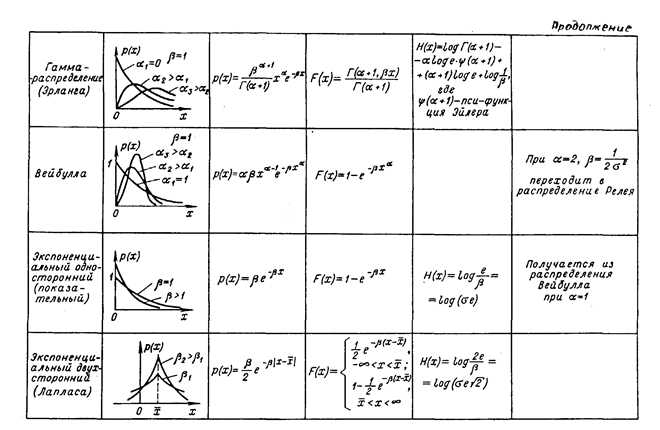
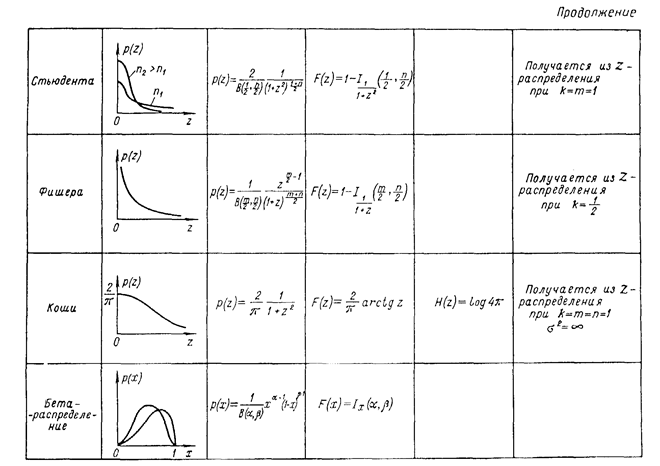
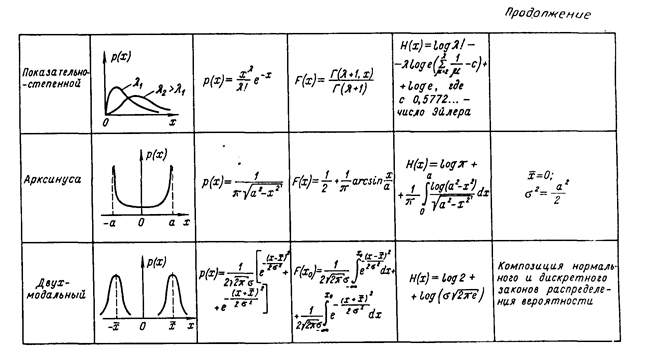
Модели эмпирических законов распределения вероятности отсчета — дифференциальная и интегральная функции распределения вероятности, как и все без исключения моменты, обладают важным качеством: будучи характеристиками случайного числа, сами они не являются случайными. Описание с их помощью отсчета или результата измерения было бы очень удобным, если бы эти характеристики можно было получить. Но на практике это невозможно, так как измерительная процедура по формулам (2), (7) не может быть повторена бесконечное число раз. Поэтому и в дальнейшем они будут использоваться только в качестве моделей. Некоторые сведения о наиболее часто используемых в метрологии моделях приведены в табл. 6.
 |
 |
Дата добавления: 2015-02-05; просмотров: 974;
