Краткие сведения из теории. Если газ находится в состоянии термодинамического равновесия, то его температура во всех точках одинакова

Если газ находится в состоянии термодинамического равновесия, то его температура во всех точках одинакова. При нарушении теплового равновесия в системе возникают потоки энергии, стремящиеся вернуть систему в состояние равновесия. Явление переноса энергии от области с большей температурой к области с меньшей температурой называется теплопроводностью. Если температура газа в разных местах различна, то в этих местах различна и средняя кинетическая энергия молекул. С течением времени, вследствие постоянных столкновений молекул, происходит перенос энергии от области с более высокой температурой к области с меньшей температурой. Этот процесс приводит к выравниванию температур. Таким образом, осуществляется процесс теплопроводности в газах.

Перенос энергии в форме теплоты подчиняется эмпирическому закону Фурье:

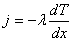, (1)

где 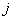− плотность теплового потока в направлении оси 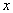(величина, численно равная количеству тепла, проходящему в секунду через единичную площадку, перпендикулярную к направлению потока тепла, измеряется в Дж/с∙м²);

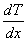
− градиент температуры, равный скорости изменения температуры на единицу длины в направлении нормали к площадке;

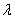− положительная постоянная, зависящая от свойств среды, проводящей тепло. Эта постоянная называется коэффициентом теплопроводности. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры. Коэффициент теплопроводности численно равен плотности теплового потока при градиенте температуры равном единице и измеряется в Дж/с∙м∙К.

Можно показать, что в газе ,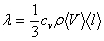

где 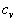− удельная теплоемкость газа при постоянном объеме ( количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме);

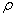− плотность газа; 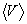− средняя скорость теплового движения молекул;

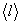− средняя длина свободного пробега.

Определим поток тепла для случая стационарного распределения температуры между двумя концентрическими цилиндрами. Диаметр внутреннего цилиндра − 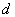, внешнего − 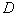. Будем считать, что длина цилиндров l>>D, поэтому тепловым потоком, идущим от торцов цилиндров, можно пренебречь. Температуры цилиндров поддерживаются при постоянных значениях 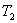и 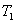. Выделим мысленно цилиндр радиуса 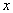, высотой 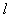. Ось

цилиндра совпадает с осью рассматриваемых цилиндров. Поток тепла, проходящий в одну секунду через боковую поверхность выделенного цилиндра:

.

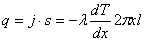Полученное дифференциальное уравнение с разделяющимися переменными легко интегрируется:

,

.

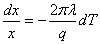
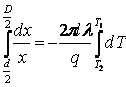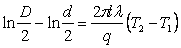Отсюда 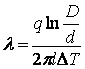, (2)

где 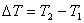− разность температур цилиндров.