Упражнение 3. Определение ускорение свободного падения с помощью оборотного маятника (метод Бесселя)

В общем случае тела произвольной формы, период колебаний зависит от момента инерции тела относительной точки подвеса, однако и в этом случае можно использовать формулу для математического маятника, вводя вместо длины математического маятника приведенную длину физического маятника, определяемую как:

l_П = J/ma;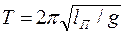

где J-момент инерции, а- расстояние между точкой подвеса осью вращения и центром масс маятника.

Применение оборотного маятника для определения ускорения свободного падения основано на зависимости периода колебаний от ускорения свободного падения и свойстве сопряженности точки подвеса. Период колебаний маятника не изменится, если его подвесить в центре качания, т.е. на расстоянии приведенной длины от первоначальной точки подвеса.

Пусть в простейшем случае маятник представляет собой стержень с насаженными на него двумя призмами точки подвеса В и массивными грузами С и Д. Перемещая грузы, можно изменить положение центра масс, можно изменить и подбирать приведенную длину маятника.

Согласно теоремы Штейнера о моментах инерции.

J = J₀ + ma²

где J₀- момент инерции относительно оси, проходящей через центр масс, а а- расстояние от призмы до центра масс . Тогда для маятника, подвешенного на призме1.

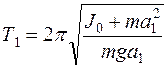
а для маятника, подвешенного на призме 2

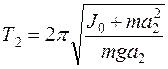
Это дает

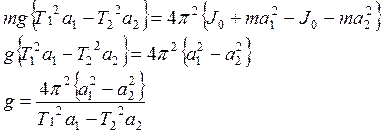
Если подобрать положение грузов или призм таким образом, чтобы расстояние между призмами было равно приведенной длине маятника, то

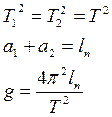
Расстояние между призмами может быть измерено с большой точностью, период колебаний также можно измерять очень точно.

В общем же случае не равных периодов

Формула Бесселя для определения величины ускорения свободного падения.