Маховое колесо

Цель работы: определить момент инерции махового колеса и момент сил трения.

Приборы и принадлежности: маховое колесо, секундомер, штангенциркуль, линейка, угольник.

Маховое колесо представляет собой массивное тело, вращающееся на подшипниках вокруг горизонтальной оси. На вал колеса радиуса r наматывается нить с подвешенным грузом массы m (рис. 16).

Опускаясь с некоторой высоты h₁, груз раскручивает колесо и, достигнув нижней точки, начинает подниматься вверх за счет запасенной кинетической энергии колеса. При отсутствии сил сопротивления высота подъема груза h₂ была бы равна h₁ в соответствии с законом сохранения механической энергии. В действительности же, ввиду действия сил трения в подшипниках, сопротивления воздуха, а также выделения тепла в нити, груз поднимается на несколько меньшую высоту. В рассматриваемом случае главной причиной потерь энергии является действие сил трения.

Известно, что если в замкнутой системе действуют неконсервативные силы (например, силы трения), то работа этих сил равна изменению полной механической энергии системы:

DE = E₂ - E₁ = A_тр.

Рассмотрим систему колесо-груз в крайних положениях h₁ и h₂, когда кинетическая энергия равна нулю, т.е. механическая энергия системы равна потенциальной энергии груза.

Тогда

DE = E₂ - E₁ = mgh₂ - mgh₁ = A_тр = -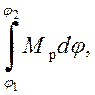

где М_тр - модуль момента сил трения. Знак «минус» в правой части указывает на то, что работа сил трения отрицательна. Интеграл берется в пределах полного угла поворота колеса при опускании и подъеме груза.

Момент сил трения можно считать практически не зависящим от скорости вращения, т.е. постоянной величиной. Следовательно.

А_{т р}= - М_тр Dj.

Пусть h₁ и h₂ отсчитываются от нижнего положения груза. Груз при движении проходит расстояние h₁+h₂, а колесо поворачивается на угол

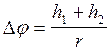
В результате

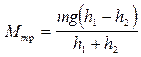
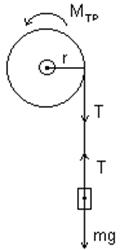
Рис. 16

На колесо действуют только две силы с отличными от нуля моментами – сила натяжения нити Т и сила трения (рис.16). Поэтому закон движения SМ_I = Je, запишется в виде:

T×r - M_тр = Je,

где e - угловое ускорение колеса.

Второй закон Ньютона для груза:

mg – T = ma,

где а – ускорение груза.

Учитывая, что тангенциальное ускорение точек обода вала равно ускорению груза (нить нерастяжима) а = а_t,

а = er.

Так как сила трения постоянна, то ускорение постоянно, т.е. применимо уравнение равноускоренного движения

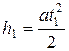
где t₁ – время опускания груза.