Выводы. 10 страница

Если уравнение неадекватно, необходимо перейти к неполной или полной квадратичной модели.

Переход к неполной квадратичной модели, в которой к правой части уравнения (5.13) добавляются слагаемые вида b_il·x_i·x_l (причем i≠l), может быть осуществлен без проведения дополнительных опытов.

Коэффициенты, учитывающие одновременное изменение двух факторов, рассчитываются по формуле:

.

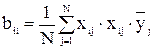Однако при этом эффекты взаимодействия различных факторов могут накладываться друг на друга. Например, при проведении опытов по матрице (табл. 5.5) коэффициенты b₁₂ и b₃₄ равны. При получении значимых коэффициентов взаимодействия можно попытаться отнести их к тому или иному взаимодействию, исходя из физического смысла, а также из сравнения коэффициентов, полученных для каждого из факторов.

Для перехода к полной квадратичной модели, включающей слагаемые вида 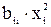, необходимо проведение дополнительных опытов.

Переход к натуральным показателям

Если уравнение адекватно, осуществляют переход от условных переменных к натуральным. Для этого уравнение (5) подставляют 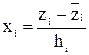и получают уравнение вида:

,

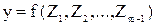которым удобнее пользоваться для расчета выходного параметра внутри исследованной области. Решение задачи интерполяции на этом заканчивается.

Расчет крутого восхождения

Если решается задача оптимизации и требуемые значения выходного параметра не достигнуты, после получения адекватного уравнения регрессии обычно принимают решение использовать метод крутого восхождения. Изменяя независимые переменные пропорционально величинам коэффициентов регрессии, условия процесса приближают к оптимальным по самому крутому пути. Восхождение начинают из нулевого уровня.

Один из факторов (обычно оказывающий наибольшее влияние на выходной параметр) принимают за базовый. Выбирают шаг движения по базовому фактору:

ΔZ_б=γ·h_б,

где γ – коэффициент, принимаемый обычно в пределах 0,3…0,9;

h_б – интервал варьирования базового фактора.

Затем рассчитывают шаги движения по факторам, пропорционально произведениям коэффициентов регрессии на интервалы варьирования:

.

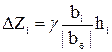Факторы планирования в опытах принимают значения

,

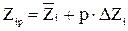где p – номер шага крутого восхождения.

Проведение опытов крутого восхождения

Крутое восхождение считается эффективным, если хотя бы в одном опыте достигнут результат, лучший по сравнению с наилучшим результатом в опытах по матрице планирования. Крутое восхождение прекращают, если уровни факторов или выходного параметра вышли за допустимые пределы либо достигнут экстремум параметра оптимизации.

3. МАТЕРИАЛЫ И ОБОРУДОВАНИЕ

Оборудование

1. Персональный компьютер.

4. ПРОГРАММА РАБОТЫ

1. Изучить методические указания.

2. Получить задание на работу.

3. Выбрать выходной параметр (критерий оптимизации) факторы планирования, составить матрицу планирования.

4. Ввести запрашиваемые данные и выполнить все необходимые этапы планирования эксперимента на персональном компьютере.

5. Сформулировать выводы по работе.

5. СОДЕРЖАНИЕ ОТЧЕТА

1. Цель работы.

2. Программа работы.

3. Индивидуальное задание.

4. Вариант классического плана эксперимента.

5. Обоснование и расчеты по планированию и обработке результатов эксперимента.

6. Выводы.

6. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Преимущества метода математического планирования эксперимента по сравнению с классическим.

2. Как производится выбор интервалов варьирования?

3. Что такое дробный факторный эксперимент?

4. Для чего производится оценка значимости коэффициентов уравнения регрессии?

5. В каких случаях используется метод крутого восхождения?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основная литература

1. Справочник по пайке / под ред. И.Е. Петрунина. – 3-е изд., перераб. и доп. – М. : Машиностроение, 2003. – 480 с.

Дополнительная литература

1. Кане, М.М. Основы научных исследований в технологии машиностроения / М.М. Кане. – М. : Высш. шк., 1987. – 231 с.

2. Основы научных исследований / под ред. В.И. Крутова, В.В. Попова. – М. : Высш. шк., 1989. – 400 с.