Выводы. 9 страница
Управление вакуумной системой осуществляется с правого пульта управления универсального вакуумного поста.
Переключение режимов работы вакуумной системы производят с помощью магнитных вентилей в следующем порядке. При создании предварительного вакуума в рабочем объеме (нажата кнопка «ПВ» на пульте управления) вентили 3 и 4 открыты, вентиль 6 закрыт. При откачке воздуха до остаточных давлений, соответствующих высокому вакууму (нажата кнопка «ВВ»), открыты вентили 4 и 6, вентиль 3 закрыт. Для создания высокого вакуума в рабочем объеме необходимо вручную открыть высоковакуумный клапан 10, в противном случае будет происходить откачка остаточных газов только из самого насоса (такой режим используется при предварительном разогреве насоса, а также при его остывании перед окончанием работы). При полной остановке прибора (нажата кнопка «0» или отпущены все кнопки) вентили 3 и 6 закрыты, вентиль 4 открыт.
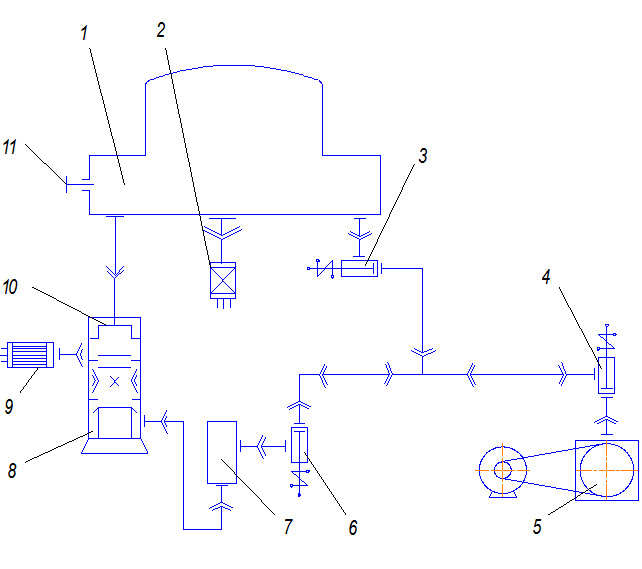
Рис. 5.3. Схема вакуумной системы универсального вакуумного поста ВУП-4:
1 – рабочий объем; 2 – термопарная манометрическая лампа типа ПМТ-4М; 3,4,6 – электромагнитный клапан; 5 – механический вакуумный насос; 7 – буферный баллон; 8 – диффузионный вакуумный насос; 9 – ионизационная манометрическая лампа ПМИ-2; 10 – высоковакуумный клапан; 11 – винт для напуска воздуха в рабочий объем
Для включения вакуумной системы:
– нажмите кнопку «Сеть». При этом должна загореться сигнальная лампочка, находящаяся рядом с кнопкой;
– проверьте положение высоковакуумного клапана и клапана напуска воздуха. Они должны быть в закрытом положении;
– нажмите кнопку «ФН», а через 2-3 минуты – кнопки «ДН» и «ВВ». При этом должны загореться соответствующие сигнальные лампочки, находящиеся над кнопками. Откройте вентиль подачи воды к диффузионному насосу;
– нажмите через 30-40 минут кнопку «ПВ» и откачайте рабочий объем до 5·10-2 – 1·10-2 мм рт. ст.
Измерение давления производите с помощью индикатора вакуума, расположенного на пульте управления, и датчика ПМТ-4М, расположенного в рабочем объеме:
а) нажмите кнопку над гравировкой «Индикатор вакуума»;
б) нажмите кнопку «ПМТ-4М» и установите ток накала согласно паспорту датчика (или по указанию учебного мастера);
в) нажмите кнопку «ФВ». Определите вакуум согласно градуированной кривой датчика и показаниям измерительного прибора.
После достижения указанного вакуума нажмите кнопку «ВВ» и откройте высоковакуумный клапан.
Замерьте высокий вакуум в рабочем объеме:
а) нажмите кнопку «ПРОГ» и выдержите в этом режиме 10-15 минут;
б) нажмите кнопку «ЭМИСС» и установите стрелку прибора на 5 мВ;
в) нажмите кнопку «НУЛЬ» и установите нуль на измерительном приборе;
г) нажмите кнопку «10-4». Если стрелка измерительного прибора показывает менее 1 мВ данного диапазона, нажмите кнопку «10-5» и т. д. Перевод показаний прибора производите умножением показаний в милливольтах соответственно на 10-4, 10-5 и т. д.
Для выключения прибора выполните следующее:
а) откачайте воздух из рабочего объема;
б) закройте высоковакуумный клапан;
в) нажмите кнопку над гравировкой «Индикатор вакуума». При этом должна погаснуть сигнальная лампочка, расположенная над кнопкой;
г) нажмите кнопку «ДН». При этом должна погаснуть сигнальная лампочка, находящаяся над кнопкой;
д) через 20-30 минут нажмите кнопки «0».
При этом должны погаснуть соответствующие лампочки; закройте вентиль подачи воды к диффузионному насосу.
ВНИМАНИЕ! Во избежание выхода из строя ионизационного вакуумметра и диффузионного насоса ЗАПРЕЩАЕТСЯ:
напуск воздуха в рабочий объем при открытом высоковакуумном клапане;
включение и использование ионизационного вакуумметра при давлении в системе выше 5·10-2 мм рт. ст.;
выключение форвакуумного насоса ранее, чем через 20 минут после отключения диффузионного насоса.
6. СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Краткие сведения об основных элементах и характеристиках вакуумных систем.
3. Схема вакуумной системы ВУП-4.
4. Результаты измерения давления при откачке и натекании (таблицы и графики).
5. Расчеты эффективной быстроты откачки, натекания и оценки достоверности по критерию Стьюдента.
6. Выводы.
7. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое вакуум?
2. Основные элементы вакуумных систем.
3. Как изменяются показания регистрирующих приборов при повышении давления в системе при использовании термопарного вакуумметра? ионизационного вакуумметра?
4. Что характеризует величина натекания?
Лабораторная работа № 3
ПОДБОР ЭМПИРИЧЕСКИХ ФОРМУЛ
1. ЦЕЛЬ РАБОТЫ
Изучить методики обработки экспериментальных данных для получения эмпирических формул.
2. ПРИНЦИПЫ И ПРИЕМЫ ПОДБОРА ЭМПИРИЧЕСКИХ ФОРМУЛ
Зависимости между параметрами, характеризующими объект, могут быть аналитическими или эмпирическими. Аналитические формулы описывают какой – либо установленный физический закон (например, закон Ома: I=U/R) и действительны в достаточно широкой области действия этого закона. Эмпирические формулы описывают полученные экспериментальные результаты и действительны лишь в тех пределах, в которых изменялись значения описываемых параметров при проведении опытов. Примеры эмпирических зависимостей: 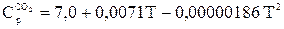 ; У=34,1-1,0х1 -3,65х2; У=0,15е
; У=34,1-1,0х1 -3,65х2; У=0,15е 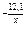 . Эмпирические формулы широко применяются в технике для описания малоизученных объектов, когда аналитические зависимости неизвестны, а также если аналитическое выражение сложное и требует громоздких вычислений.
. Эмпирические формулы широко применяются в технике для описания малоизученных объектов, когда аналитические зависимости неизвестны, а также если аналитическое выражение сложное и требует громоздких вычислений.
Эмпирические формулы должны быть по возможности более простыми и точно описывать экспериментальные данные. Процесс подбора эмпирических формул состоит из двух этапов: 1) выбор вида формулы; 2) расчет коэффициентов формулы. Если кривая имеет резкие перегибы или состоит из отдельных участков, целесообразно подбирать формулы по участкам, однако необходимо четко определять координаты пограничных точек перехода от одной формулы к другой.
Подбор эмпирических формул следует начинать с наиболее простых выражений. Многие объекты описываются линейной функцией вида у = ах + b. Причем в ряде случаев это может быть связано не только с физической сущностью объекта, но и с недостаточной его изученностью, большим разбросом экспериментальных результатов, а также удобством расчета. Коэффициенты а и b определяются по экспериментальным результатам. Обычно используют метод наименьших квадратов, достаточно простой и точный. Этот метод исходит из требования, чтобы сумма квадратов отклонений ординат экспериментальных точек от прямой, описываемой искомым уравнением, была минимальной. Расчет коэффициентов линейной модели проводят по формулам:
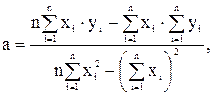
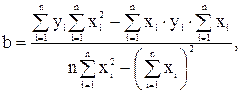 (5.7)
(5.7)
где xi, yi – значения х и у по результатам i-го измерения (или i-го опыта);
n – общее количество измерений (опытов).
Точность описания экспериментальных данных линейной зависимостью оценивается по величине коэффициента корреляции r:
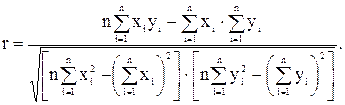 (5.8)
(5.8)
Чем ближе r к 1, тем ближе зависимость у=f(х) к линейной. Если |r| < 0,5, зависимость следует признать нелинейной. В зависимости от вида экспериментальной кривой ее аппроксимируют различными функциями (рис. 5.4). Для определения коэффициентов эмпирических формул можно использовать метод выравнивания, при котором переменные х и у заменяются другими, между которыми существует линейная зависимость. Например, если искомая зависимость имеет вид y=a·xC, то логарифмируя правую и левую части, получим ln y=ln a+Cln x или Y=А+CX. Теперь коэффициенты А и С могут быть найдены методом наименьших квадратов по формуле (1), в которую вместо 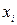 и
и 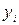 подставляют
подставляют 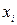 =ln
=ln 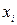 и
и 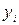 =ln
=ln 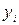 . Коэффициент С определяется сразу, а для определения а проводят потенцирование а = еA. Приемы замены для различных функций указаны в справочниках. Для оценки точности описания экспериментальных данных может быть использован коэффициент корреляции, рассчитанный по формуле (5.8) с подстановкой Xi и Yi. Чем ближе |r| к 1, тем лучше описываются экспериментальные данные выбранным видом зависимости.
. Коэффициент С определяется сразу, а для определения а проводят потенцирование а = еA. Приемы замены для различных функций указаны в справочниках. Для оценки точности описания экспериментальных данных может быть использован коэффициент корреляции, рассчитанный по формуле (5.8) с подстановкой Xi и Yi. Чем ближе |r| к 1, тем лучше описываются экспериментальные данные выбранным видом зависимости.
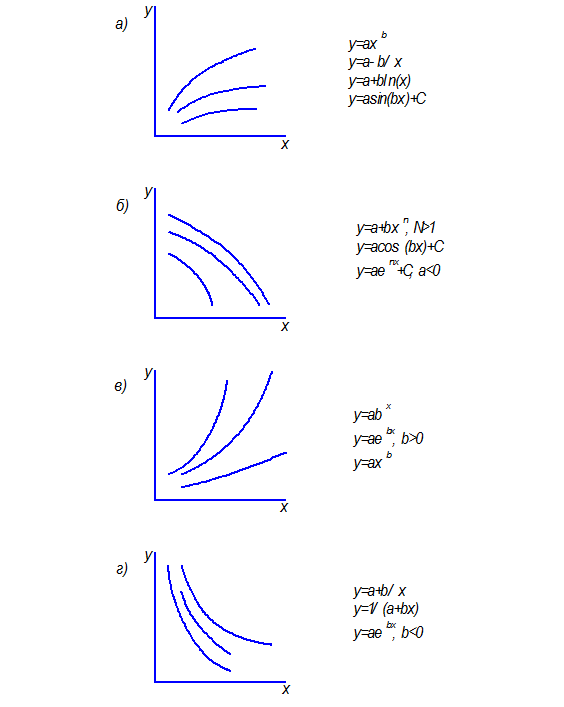
Рис. 5.4. Типовые графики и некоторые аппроксимирующие их выражения
Кроме метода наименьших квадратов могут использоваться и другие, например, метод избранных точек. В этом случае на плавной кривой намечается столько точек, сколько неизвестных коэффициентов в выбранной формуле (рис. 5.5). Их координаты подставляются в формулу, и решается полученная система уравнений. Например, в рассматриваемом случае
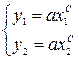 или
или 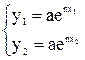 ,
,
где (x1,y2) и (x1,y2) – координаты первой и второй избранных точек.
Для подбора эмпирических формул могут также использоваться неравномерные координатные сетки и эталонные кривые. В последнее время при подборе эмпирических формул все чаще применяются ЭВМ (расчет коэффициентов при этом обычно основан на методе наименьших квадратов и замене переменных).
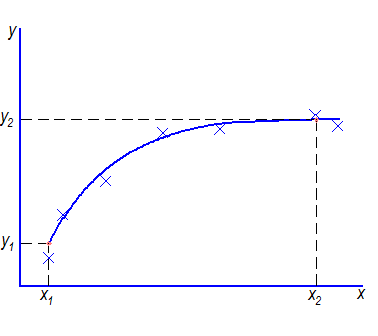
Рис. 5.5. Метод избранных точек: x-экспериментальные точки; •-избранные точки
3. МАТЕРИАЛЫ И ОБОРУДОВАНИЕ
Оборудование
1. Персональный компьютер.
4. ПРОГРАММА РАБОТЫ
1. Получить задание на работу (набор экспериментальных данных), построить график y=f(x) и выбрать вид функции.
2. Подобрать эмпирическую формулу, описывающую представленные данные, одним из известных способов без использования ЭВМ (кроме микрокалькулятора).
3. Продолжить работу в режиме диалога с ЭВМ: подобрать несколько вариантов эмпирической формулы и выбрать из них наиболее подходящий.
5. СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Программа работы.
3. Индивидуальное задание.
4. Первоначально подобранная эмпирическая формула с описанием этапов подбора.
5. Варианты эмпирических формул, подобранные с помощью ЭВМ, построенные по формулам графики с указанием заданных экспериментальных точек, коэффициенты корреляции различных зависимостей.
6. Выводы, приводящие обоснование выбранного варианта эмпирической формулы.
6. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие виды формул Вы знаете?
2. Что такое метод наименьших квадратов?
3. Как подобрать эмпирическую формулу по имеющимся экспериментальным данным?
4. Что такое коэффициент корреляции?
5. Какие виды зависимостей или функций наиболее часто используются при подборе эмпирических формул?
Лабораторная работа № 4
ПЛАНИРОВАНИЕ И ОБРАБОТКА РЕЗУЛЬТАТОВ
МНОГОФАКТОРНЫХ ЭКСПЕРИМЕНТОВ
1. ЦЕЛЬ РАБОТЫ
Изучить основные понятия и приобрести практические навыки математического планирования и обработки результатов много факторных экспериментов.
2. ОСНОВНЫЕ ЭТАПЫ ФАКТОРНОГО ПЛАНИРОВАНИЯ
ЭКСПЕРИМЕНТА
Технологические процессы, в частности сварка и пайка, характеризуются одновременным воздействием на изделие многих технологических факторов. Применение вместо классического метода математического планирования эксперимента позволяет при исследовании технологических процессов сократить время и повысить точность результатов, оптимизировать технологические режимы, а также создавать системы автоматического управления технологическими процессами.
Математическое планирование эксперимента – это процедура выбора числа и условий постановки опытов, необходимых и достаточных для решения данной задачи с требуемой точностью, методов математической обработки их результатов и принятия решений.
Основными этапами наиболее распространенного варианта факторного планирования эксперимента являются следующие.
Выбор выходного параметра и факторов планирования
Количество параметров, характеризующих объект исследования, теоретически бесконечно. От правильного выбора выходного параметра (а при поиске наилучших условий функционирования объекта – критерия оптимизации) и факторов, изменяемых при проведении эксперимента (факторов планирования), зависит успех исследования. Выбор выходного параметра и факторов планирования производится на основании сведений о изучаемом и родственных объектах (так называемой априорной информации).
Выбранный выходной параметр обязан отвечать условию однозначности, т.е. заданному выбору значений факторов должно соответствовать одно значение выходного параметра (с учетом погрешности эксперимента). Критерий оптимизации должен эффективно оценивать функционирование всего процесса. Целесообразно также, чтобы критерий имел физический смысл, был простым, легко вычисляемым и позволял осуществлять всевозможные комбинации факторов. Качество процесса часто характеризуется несколькими параметрами. Однако движение к оптимуму упрощается, если выбран только один параметр оптимизации (остальные показатели в этом случае могут служить ограничениями).
Факторы планирования должны быть управляемыми, не взаимосвязанными, количественными. Погрешность измерения фактора должна быть в 3-5 раз меньше погрешности выходного параметра. Следует стремиться к учету всех факторов, существенно влияющих на выходной параметр. Однако с увеличением количества факторов либо возрастает количество опытов, либо уменьшается точность математической модели.
Выбор среднего уровня фактора 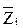
Обычно в качестве среднего уровня принимают значение, соответствующее наилучшему с точки зрения предшествующего знания об объекте значению выходного параметра. Если это значение близко к границе возможной области изменения фактора, средний уровень выбирают с некоторым сдвигом от наилучших условий.
Выбор интервалов варьирования hi
На первом этапе эксперимента обычно получают линейную модель объекта. Для построения такой модели факторы при проведении опытов должны принимать только два значения – верхний и нижний уровни. Интервал варьирования – разность между значениями фактора на среднем и верхнем (нижнем) уровнях.
Интервал варьирования должен быть больше ошибки определения уровня фактора, но уровни фактора не должны выходить за границы области исследования. Значение факторов в эксперименте:
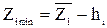 ;
;
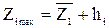 .
.
Переход от натуральных переменных Zi к условным переменным Xi
Для упрощения записи условий эксперимента и расчетов при обработке экспериментальных данных натуральные переменные заменяют кодированными (условными). Для количественных факторов замена проводится по формулам
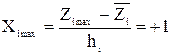 ,
,
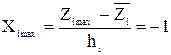 .
.
Составление матрицы планирования
Матрица планирования - это таблица, описывающая условия проведения опытов, в которой строки соответствуют различным опытам, а столбцы - значениям факторов. Уровни факторов в матрице (+1 или –1) часто обозначают просто знаками (+ или – ). При полном факторном эксперименте реализуются все возможные сочетания уровней факторов (табл. 5.2, 5.3).
Таблица 5.2
Два фактора. Полный факторный эксперимент 22
| Номер опыта | Значения факторов | |
| X1 | X2 | |
| – | – | |
| + | – | |
| – | + | |
| + | + |
Таблица 5.3
Три фактора. Полный факторный эксперимент 23
| Номер опыта | Значение факторов | ||
| X1 | X2 | X3 | |
| – | – | + | |
| – | + | – | |
| + | – | – | |
| + | + | + | |
| – | – | – | |
| – | + | + | |
| + | – | + | |
| + | + | – |
Для сокращения количества опытов обычно предпочитают дробный факторный эксперимент, т.е. не полный перебор всех возможных сочетаний уровней факторов, а строго определенное их сочетание, позволяющее рассчитать коэффициенты математической модели. Однако с повышением дробности матрицы уменьшается точность расчета коэффициентов модели и возможность установления совместного действия нескольких факторов. Для составления матрицы планирования существуют специальные правила. В табл. 5.4 – 5.7 приведены возможные варианты матриц планирования для 3-6 факторов и числа опытов не более 6.
Таблица 5.4
Три фактора. Дробный факторный эксперимент 23-1
| Номер опыта | Значение факторов | ||
| X1 | X2 | X3 | |
| – | – | – | |
| + | + | – | |
| – | + | + | |
| + | – | + |
Таблица 5.5
Четыре фактора. Дробный факторный эксперимент 24-1
| Номер опыта | Значение факторов | |||
| X1 | X2 | X3 | X4 | |
| – | – | – | – | |
| + | + | – | – | |
| + | – | + | – | |
| + | – | – | + | |
| – | + | + | – | |
| – | + | – | + | |
| – | – | + | + | |
| + | + | + | + |
Таблица 5.6
Пять факторов. Дробный факторный эксперимент 25-2
| Номер опыта | Значения факторов | ||||
| X1 | X2 | X3 | X4 | X5 | |
| – | – | – | – | – | |
| + | + | – | – | – | |
| – | – | + | + | – | |
| + | – | + | – | + | |
| – | + | + | – | + | |
| + | – | – | + | + | |
| – | + | – | + | + | |
| + | + | + | + | – |
Таблица 5.7
Шесть факторов. Дробный факторный эксперимент 26-3
| Номер опыта | Значения факторов | |||||
| X1 | X2 | X3 | X4 | X5 | X6 | |
| – | – | – | – | – | – | |
| + | – | + | – | – | + | |
| + | – | – | + | + | – | |
| – | + | + | – | + | – | |
| – | + | – | + | – | + | |
| + | + | + | + | – | – | |
| + | + | – | – | + | + | |
| – | – | + | + | + | + |
Одновременно с матрицей значений условных переменных составляется и матрица значений натуральных переменных в опытах.
Проведение эксперимента
Опыты по матрице планирования необходимо выполнять в случайном порядке, каждый опыт в одних и тех же условиях повторять несколько раз.
Проверка воспроизводимости опытов
По результатам повторных опытов вычисляют в каждой строке матрицы:
– среднее арифметическое
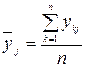 , (5.9)
, (5.9)
где n – количество опытов, выполненных при одинаковых условиях
(j строка);
ykj – значение выходного параметра в k-ом опыте j-строка;
– дисперсию:
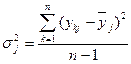 . (5.10)
. (5.10)
Проверяют однородность дисперсий. Если число повторных опытов во всех строках матрицы одинаково, проверка производится по критерию Кохрена:
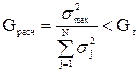 , (5.11)
, (5.11)
где Gрасч – рассчитанное значение критерия Кохрена;
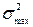 – максимальная из всех построчных дисперсий;
– максимальная из всех построчных дисперсий;
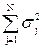 – сумма построчных дисперсий во всех N строках матрицы;
– сумма построчных дисперсий во всех N строках матрицы;
Gт – табличное значение критерия Кохрена (табл. 5.8).
Таблица 5.8
Значение критерия Кохрена для различного числа опытов
при доверительной вероятности 0,95
| Число строк матрицы планирования | Число опытов в каждой строке матрицы | |||
| 0,907 | 0,768 | 0,684 | 0,629 | |
| 0,680 | 0,516 | 0,438 | 0,391 |
Если расчетное значение критерия Кохрена больше допустимого, математическую модель строить нельзя. Необходимо повторить опыты данной строки либо перестроить схему эксперимента с целью повышения его точности.
Для дальнейших расчетов определяют дисперсию воспроизводимости:
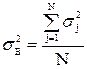 . (5.12)
. (5.12)
Расчет коэффициентов уравнения регрессии
Вследствие воздействия случайных факторов результаты опытов, проведенных в одних и тех же условиях (с точки зрения исследователя), будут отличаться друг от друга. Поэтому после их обработки можно указать только наиболее вероятное значение выходного параметра при данных значениях факторов. В таких случаях связь между выходными параметрами и факторами называют корреляционной, а описывающее ее уравнение - уравнением регрессии. При построении линейной модели объекта уравнение регрессии имеет вид:
y=b0+b1x1+b2x2+…+bixi+…bm-1·xm-1 (5.13)
Коэффициенты уравнения регрессии рассчитывают по формуле:
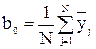 ;
; 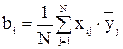 , (5.14)
, (5.14)
где xij – значение i-того фактора в j-й строке матрицы планирования.
Оценка значимости коэффициентов уравнения регрессии
Оценка значимости коэффициентов проводится для отбрасывания членов уравнения (5.13), незначительно влияющих на выходной параметр. В результате упрощаются расчеты.
Определяется доверительный интервал
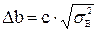 , (5.15)
, (5.15)
где 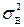 - рассчитанная по формуле (5.12) дисперсия воспроизводимости;
- рассчитанная по формуле (5.12) дисперсия воспроизводимости;
с – постоянная, зависящая от числа строк матриц и количества опытов в каждой строке (табл. 5.9).
Таблица 5.9
Коэффициент С для расчета доверительного интервала
| Количество строк в матрице | Количество опытов, проведенных в условиях каждой строки | |||
| 1,15 | 1,06 | 1,03 | 1,02 | |
| 0,81 | 0,75 | 0,73 | 0,72 |
Значимость коэффициентов уравнения регрессии определяется из условия |bi|>Δb. Если абсолютная величина коэффициента регрессии bi меньше доверительного интервала, фактором xi можно пренебречь.
Проверка адекватности уравнения регрессии
Определяется дисперсия адекватности:
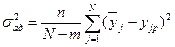 . (5.16)
. (5.16)
где n – число параллельных опытов;
N – количество строк матрицы планирования;
m – количество коэффициентов уравнения (5.13), считая b0;
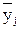 и yjр – среднее экспериментальное и рассчитанное по уравнению (5.13) значение выходного параметра для условий j-й строки матрицы.
и yjр – среднее экспериментальное и рассчитанное по уравнению (5.13) значение выходного параметра для условий j-й строки матрицы.
Определяют критерий Фишера:
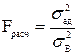 .
.
Уравнение (5.13) считается адекватным, если Fрасч<Fтабл (табл. 5.10).
Таблица 5.10
Значение критерия Фишера при доверительной вероятности 0,95
| Число степеней свободы дисперсии воспроизводимости fВ=N(n-1) | Число степеней свободы дисперсии адекватности fад=N-m | ||||
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | |
| 4,5 | 3,6 | 3,2 | 2,9 | 2,8 | |
| 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | |
| 4,2 | 3,3 | 2,9 | 2,7 | 2,5 |
Дата добавления: 2015-01-29; просмотров: 1965;
