Математические модели на метауровне

Математические модели в технологических системах довольно разнообразны.

Математические модели с использованием целочисленного программирования

Для создания технологических структур из РТК необходимо приобрести n PTK для участка. Для этого выделен фонд в сумме N рублей. Стоимость РТК j-ro типа — Cj, а производительность — aj, j = 1,n. Требуется выбрать РТК, обеспечивающие максимальную суммарную производительность в пределах установленного денежного лимита N. Математическая модель: (13.8)

где x = (x1, x2, ..., xj, …, xn); aj 0; Cj 0; N > 0 — целые числа.

Решение ведется методом ветвей и границ.

Если отбросим требования целочисленности, переменные aj, Cj изменяются непрерывно на отрезке [0, 1]. Решение такой непрерывной задачи будет верхней границей (так как определяется максимум) множества значений целевой функции на соответствующем подмножестве решения. Алгоритм решения непрерывной задачи состоит в следующем. Упорядочим коэффициенты a1, a2, ..., aj ... ап порядке убывания величин λj = aj /Cj и соответственно этому порядку нумеруем переменные и параметры задачи.

Процедура разбиения (методом ветвей и границ) допустимого множества G, задаваемого ограничениями, такова: разбивают G на два подмножества G1 и G2, первому подмножеству принадлежат все решения с х1=1, а второму — с x1 = 0. Далее каждое из подмножеств G1 и G2 опять разбивают на два: в первом x1 = 1, во втором х1 = 0 и т. д.

На каждом шаге очередного разбиения выбирают подмножество, которому соответствует максимальное значение оценки. Поиск решения заканчивают, если на некотором шаге получают допустимое решение значения целевой функции, на котором шаг будет наибольшим по сравнению с оценками для всех подмножеств — кандидатов на разбиение.

Математические модели с использованием систем массового обслуживания

Эти системы основаны на марковском случайном процессе. Физическая система S с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом [38]. Тогда в системе S протекает случайный процесс, который называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени t0 и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время τ система S окажется в состоянии S1 или сохранит состояние S0 и т. .

Таким образом, в марковском случайном процессе "будущее" зависит от "прошлого" только через "настоящее".

Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, удобно будет представлять, что все переходы системы S из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему S из состояния в состояние, — простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".

Если система S находится в каком-то состоянии Si, из которого есть непосредственный переход в другое состояние Sj (стрелка, ведущая из Sj в Sj на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии Sj, действует простейший поток событий, приводящий ее по стрелке Si – Sj. Как только появится первое событие этого потока, происходит "перескок" системы из Si в Sj.

Для наглядности очень удобно представлять граф состояний. Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы будут:

S0 — оба узла исправны;

S1 — первый узел ремонтируется, второй исправен;

S2 — второй узел ремонтируется, первый исправен;

S3 — оба узла ремонтируются.

Интенсивность потоков событий, переводящих систему из состояния в состояние, вычисляется при условии, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии So. Какой поток событий переводит ее в состояние S1? Очевидно, поток отказов первого узла. Его интенсивность λ1 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из Si в Sj? Очевидно, поток "окончаний ремонтов" первого узла. Его интенсивность μ1 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.

Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.

В самом деле, пусть рассматривается система S, имеющая n возможных состояний S1, S2, …, Sn. Назовем вероятностью i-го состояния вероятность pi(t) того, что в момент t система будет находиться в состоянии Sj. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице: (13.9)

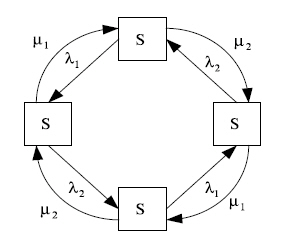
Рис. 13.2. Размеченный граф

Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний pi(t) как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова — особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.

Математические модели с использованием сетей Петри

Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма, асинхронности и иерархичности.

На рис. 13.3 приводится сети Петри, где Р — конечное непустое множество позиций (состояний); Т — конечное непустое множество переходов (событий), причем p P и ti T; F: Р x Т — {0, 1, 2, ...}; Н: Т x Р {0, 1, 2, ...} — функции входных и выходных инциденций; μ0 : Р {0, 1, 2, ...} — начальная маркировка. Вершины сети p P изображены кружками, а вершины ti T — черточками (баркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции μ: Р {0, 1, 2, ...}. Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переход t может сработать при маркировке μ, если он является возбужденным:

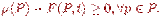(13.10)

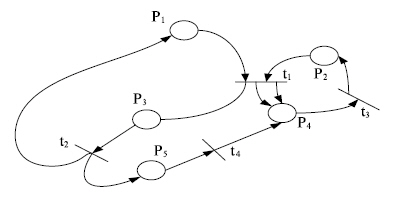
Рис. 13.3. Сеть Петри

Данное условие показывает, что в каждой входной позиции перехода t число маркеров не меньше веса дуги, соединяющей эту позицию с переходом. В результате срабатывания перехода t, удовлетворяющего условию (13.10), маркировку μ заменяют маркировкой μ' по следующему правилу: (13.11)

По этому правилу в результате срабатывания из всех входных позиций перехода t изымается F(p,t) маркеров и в каждую выходную позицию добавляется H(t,p) маркеров. Это означает, что маркировка μ' непосредственно достижима из маркировки μ. Функционирование сети Петри — последовательная смена маркировок в результате срабатывания возбужденных переходов.

Состояние сети в данный момент времени определяется ее текущей маркировкой. Важная характеристика сети Петри — граф достижимости, с помощью которого описываются возможные варианты функционирования сети. Такой граф имеет вершины, которые являются возможными маркировками. Маркировки μ и μ' соединяются в направлении t дугой, помеченной символами перехода t T или μt μ'. Маркировка μ' такая последовательность переходов: τ = t1, t2, ..., tk является достижимой из маркировки μ, если существует, что μt1μ't2 ... μ tk μ.

В качестве примера рассматривается сеть Петри, изображенная на рис. 4.3.

N = (Р, Т, F, Н, μ0), где Р = {Р1, Р2, Р3, Р4, Р5},

T = {t1, t2, t3, t4, t5}, μ0 = (1, 1, 0, 0, 0). Функции F и Н заданы матрицами

P1 P2 P3 P4 P5

H = t1 0 0 1 2 0

t2 1 0 0 0 1

t3 1 1 0 0 0

t4 0 0 0 1 0

t1 t2 t3 t4

F = P1 1 0 0 0

P2 1 0 0 0

P3 0 1 0 0

P4 0 0 1 0

P5 0 0 0 1

Фрагмент графа достижимости для сети Петри приведен на рис. 13.4.

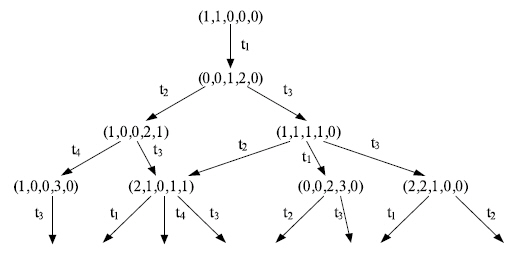
Рис. 13.4. Фрагмент графа достижимости сети Петри