Математические модели на микроуровне

Модели на микроуровне используются для исследования напряженного состояния деталей конструкции и для расчетов их на прочность. Напряженное состояние деталей конструкции в зависимости от геометрии исследуемого узла, вида приложенной нагрузки и свойств материала описывается дифференциальными уравнениями различного вида. Любое из этих уравнений может быть получено из общего квазигармонического уравнения (13.4)

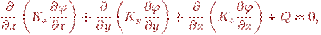
где х, у, z — пространственные координаты; — искомая непрерывная функция; Кх, Ку, Kz — коэффициенты; Q — внешнее воздействие.

В двумерном случае при Кх = Kv = 1 уравнение (13.4) сводится к уравнению, которое описывает напряженное состояние, возникающее в поперечном сечении упругого однородного стержня под воздействием крутящего момента М: (13.5)

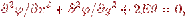
где Е — модуль сдвига материала стержня; θ — угол закручивания на единицу длины, — функция, связанная с напряжениями сдвига τх и τу уравнениями (13.6)

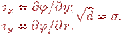
В уравнение (13.6) в явном виде не входит крутящий момент, связанный с искомой функцией напряжения уравнением (13.7)

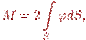
где S — площадь рассматриваемого сечения.

Точное решение краевых задач получают только в частных случаях. Поэтому реализация таких моделей заключается в использовании различных приближенных моделей. Широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток. Одним из наиболее популярных методов решения краевых задач в САПР является метод конечных элементов.