Трехмерное аффинное преобразование

Запишем в виде формулы:

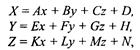где А, В,..., Ν— константы.

Дадим также запись в матричной форме:

Для трехмерного пространства любое аффинное преобразование также может быть представлено последовательностью простейших операций. Рассмотрим их.

1. Сдвиг осей координат соответственно на dx, dy, dz:

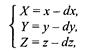
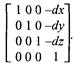
2. Растяжение/сжатие на к_x, к_y, к_z.

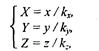
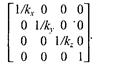
3. Повороты. Можно сказать, что в трехмерном пространстве существует больше разновидностей поворота, сравнительно с двумерным пространством. Рассмотрим несколько частных случаев поворота.

Поворот вокруг оси xна угол φ (рис. 2. 12).

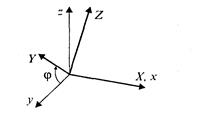
Рис. 2.12. Поворот вокруг оси X

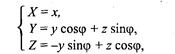
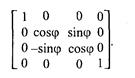
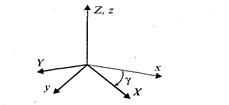
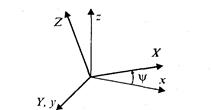Поворот вокруг оси у на угол ψ (рис. 2. 13, сверху).

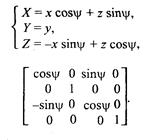
Поворот вокруг оси z на угол γ (рис. 2. 13, снизу).

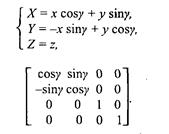
Рис. 2.13. Поворот вокруг осей y и z